A coil in the shape of square is placed in a variable magnetic field, which varies at the rate of dB /dt shown in figure. The magnitude of emf between points a and d along path abcd will be
[(L22)(dBdt)]
[L2(dBdt)]
[−2L2(dBdt)]
[3(L22)(dBdt)]
To find the magnitude of the emf (electromotive force) between points A and D along the path ABCD in a square coil placed in a variable magnetic field, we can follow these steps:
Step 1: Understand the Geometry of the Coil
The coil is in the shape of a square. Let's denote the side length of the square as L. The area A of the square coil can be calculated as:
A=L2
Hint: Remember that the area of a square is calculated by squaring the length of one of its sides.
Step 2: Use Faraday's Law of Electromagnetic Induction
According to Faraday's law, the induced emf E in a closed loop is given by the negative rate of change of magnetic flux Φ through the loop:
E=−dΦdt
Hint: The induced emf is related to how quickly the magnetic flux through the coil is changing.
Step 3: Calculate the Magnetic Flux
The magnetic flux Φ through the coil is given by:
Φ=B⋅A⋅cos(θ)
where B is the magnetic field strength, A is the area of the coil, and θ is the angle between the magnetic field and the normal to the surface of the coil. In this case, since the magnetic field is perpendicular to the area of the coil, θ=0∘ and cos(0)=1:
Φ=B⋅L2
Hint: The angle θ is important; if the field is perpendicular, the cosine term simplifies to 1.
Step 4: Differentiate the Magnetic Flux
Now, we differentiate the magnetic flux with respect to time:
dΦdt=d(B⋅L2)dt=L2dBdt
Hint: When differentiating a product, remember that if one factor changes with time, it affects the overall product.
Step 5: Substitute into Faraday's Law
Substituting the expression for dΦdt into Faraday's law gives:
E=−dΦdt=−L2dBdt
Hint: The negative sign indicates the direction of the induced emf according to Lenz's law, but we are interested in the magnitude.
Step 6: Final Expression for the Magnitude of the EMF
The magnitude of the induced emf is:
|E|=L2∣∣∣dBdt∣∣∣
Hint: The magnitude is always a positive value, so we can drop the negative sign.
Conclusion
Thus, the magnitude of the emf between points A and D along the path ABCD is given by:
|E|=L2∣∣∣dBdt∣∣∣
This expression represents the induced emf in the square coil due to the change in the magnetic field.
The coil is in the shape of a square. Let's denote the side length of the square as L. The area A of the square coil can be calculated as:
A=L2
According to Faraday's law, the induced emf E in a closed loop is given by the negative rate of change of magnetic flux Φ through the loop:
E=−dΦdt
The magnetic flux Φ through the coil is given by:
Φ=B⋅A⋅cos(θ)
where B is the magnetic field strength, A is the area of the coil, and θ is the angle between the magnetic field and the normal to the surface of the coil. In this case, since the magnetic field is perpendicular to the area of the coil, θ=0∘ and cos(0)=1:
Φ=B⋅L2
Now, we differentiate the magnetic flux with respect to time:
dΦdt=d(B⋅L2)dt=L2dBdt
Substituting the expression for dΦdt into Faraday's law gives:
E=−dΦdt=−L2dBdt
The magnitude of the induced emf is:
|E|=L2∣∣∣dBdt∣∣∣
Thus, the magnitude of the emf between points A and D along the path ABCD is given by:
|E|=L2∣∣∣dBdt∣∣∣
Topper's Solved these Questions
Similar Questions
A coil having 500 square loops each of side 10 cm is placed normal to a magnetic flux which increases at the rate of 1.0 tesla/second. The induced e.m.f. in volts is
View SolutionA current - carrying loop is shown in the figure. The magnitude of the magnetic field produced at a point O is
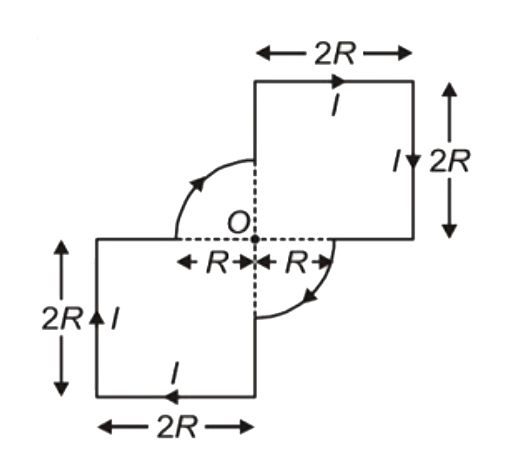
View SolutionA conducting wire carrying current I is shown in the figure. The magnitude of magnetic field at the point P will be

View SolutionA circular coil of radius R is moving in a magnetic field B with a velocity v as shown in the figure. The emf induced across the diametrically opposite points X and Y is

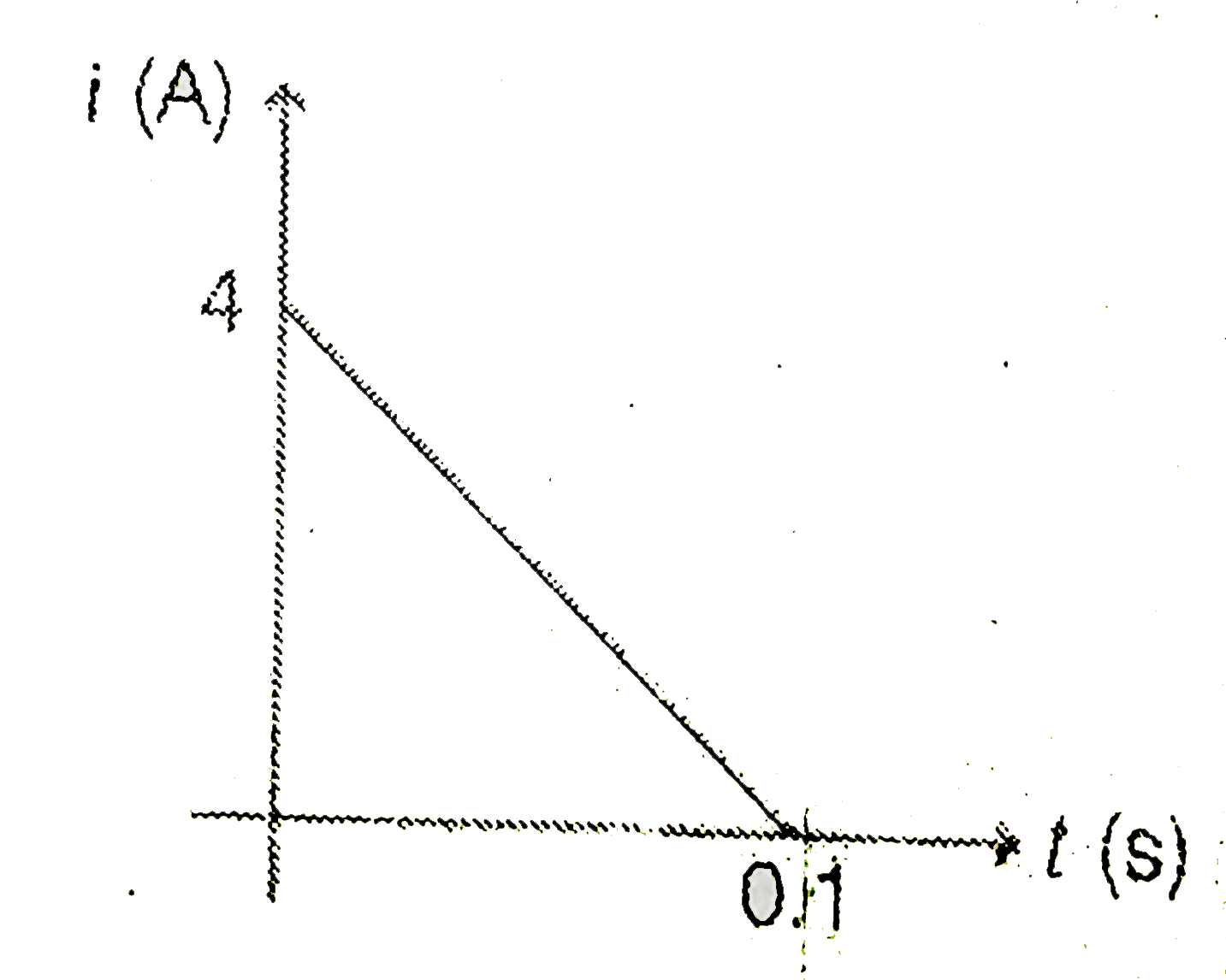
View SolutionSome magnetic flux is changed from a coil resistance 10Ω. As a result an induced current developed in it which varies with time as shown figure, The magnitude of changes f in flux through the coil (in webers) is
View SolutionA coil having N turns carry a current I as shown in the figure. The magnetic field intensity at point P is
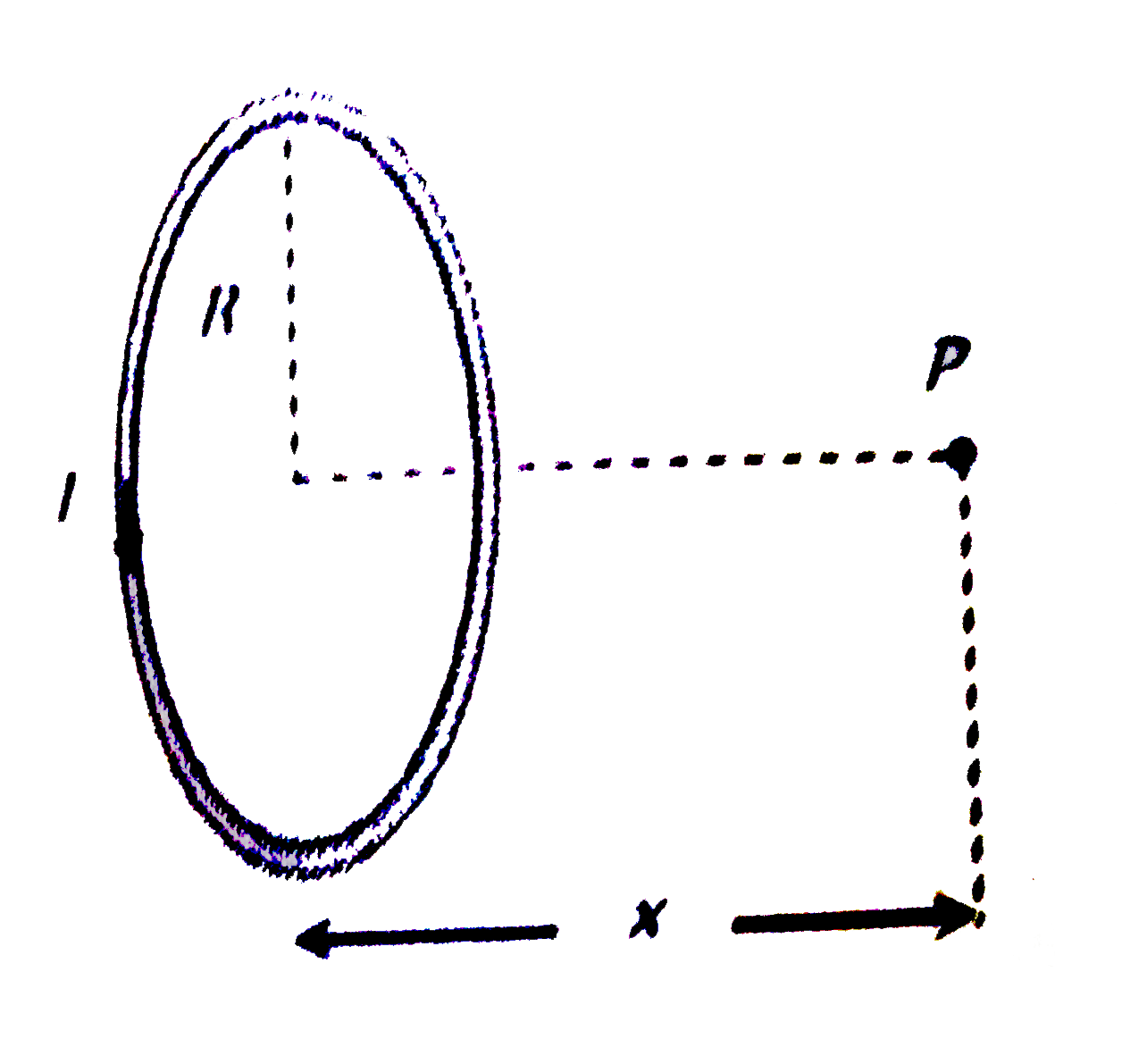
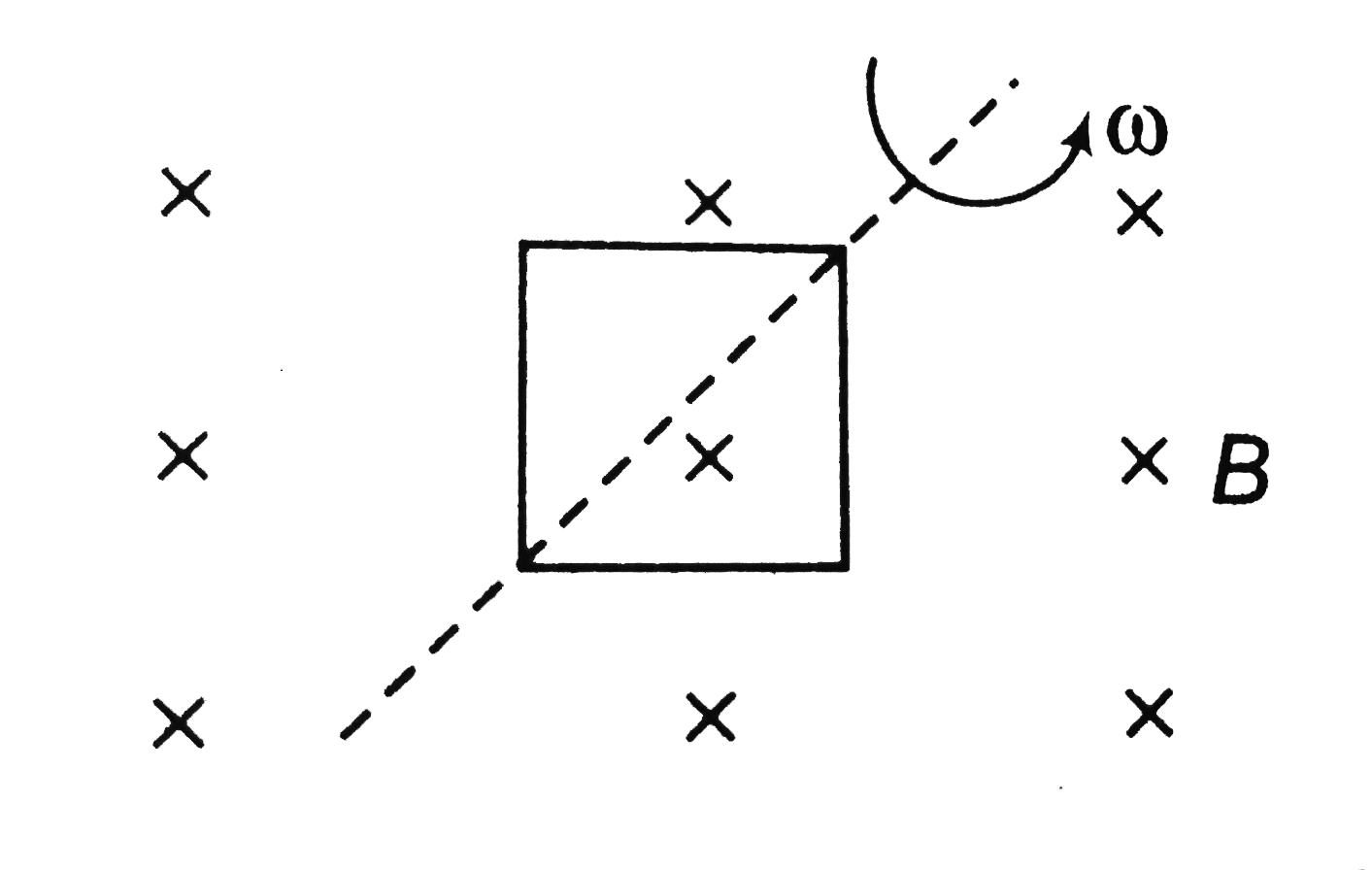
View SolutionA square loop of side b is rotated in a constant magnetic field B at angular frequency ω as shown in the figure. What is the emf induced in it?
View SolutionA coil formed by wrapping 50 turns of wire in the shape of a square is positioned in a magnetic field so that the normal to the plane of the coil makes an angle of 30∘. with the direction of the field. When the magnetic field is increased uniformly from 200μT to 600μT in 0.4s, an emf of magnitude 80.0 mV is induced in the coil. What is the total length of the wire?
View SolutionFigure shows a square loop made from a uniform
wire. Find the magnetic field at the centre of the square
if a battery is connected between the points A and C.

View SolutionA coil is placed in a constant magnetic field. The magnetic field is parallel to the plane of the coil as shown in Fig. 3.28. Find the emf induced in the coil if B increasing.

View Solution