in series R-L-C circuit at resonance, which of the following is correct?
(4f2LC=0.5)
(XL−XC)=0
Minimum power dissipation occurs at resonance
Both (1) & (2) are correct
To solve the question regarding the behavior of a series RLC circuit at resonance, we can follow these steps:
1. Understanding Resonance in RLC Circuit:
In a series RLC circuit, resonance occurs when the inductive reactance (X_L) is equal to the capacitive reactance (X_C). At this point, the circuit behaves purely resistively.
2. Setting Up the Resonance Condition:
At resonance, we have:
XL=XC
Where:
- XL=ωL (Inductive reactance)
- XC=1ωC (Capacitive reactance)
3. Equating Inductive and Capacitive Reactance:
Setting the two reactances equal gives us:
ωL=1ωC
4. Rearranging the Equation:
Multiplying both sides by ωC leads to:
ω2LC=1
5. Substituting ω:
We know that ω=2πf, where f is the frequency. Substituting this into the equation gives:
(2πf)2LC=1
Simplifying this results in:
4π2f2LC=1
6. Understanding Power Dissipation:
The power dissipated in the circuit can be expressed as:
P=VrmsIrmscosϕ
Where ϕ is the phase angle. At resonance, since XL−XC=0, the phase angle ϕ becomes 0, and thus cosϕ=1.
7. Conclusion:
Therefore, the correct statement at resonance in a series RLC circuit is:
XL−XC=0
This corresponds to option B in the question.
Final Answer:
The correct answer is: XL−XC=0 (Option B).
In a series RLC circuit, resonance occurs when the inductive reactance (X_L) is equal to the capacitive reactance (X_C). At this point, the circuit behaves purely resistively.
At resonance, we have:
XL=XC
Where:
- XL=ωL (Inductive reactance)
- XC=1ωC (Capacitive reactance)
Setting the two reactances equal gives us:
ωL=1ωC
Multiplying both sides by ωC leads to:
ω2LC=1
We know that ω=2πf, where f is the frequency. Substituting this into the equation gives:
(2πf)2LC=1
Simplifying this results in:
4π2f2LC=1
The power dissipated in the circuit can be expressed as:
P=VrmsIrmscosϕ
Where ϕ is the phase angle. At resonance, since XL−XC=0, the phase angle ϕ becomes 0, and thus cosϕ=1.
Therefore, the correct statement at resonance in a series RLC circuit is:
XL−XC=0
This corresponds to option B in the question.
The correct answer is: XL−XC=0 (Option B).
Topper's Solved these Questions
Similar Questions
In series LCR circuit at resonance
View SolutionIn an L-C-R series, AC circuit at resonance
View SolutionThe series RLC circuit in resonance is called:
View SolutionIn L−C−R series circuit
View SolutionA series L-C-R circuit is operated at resonance . Then
View SolutionFor a series L - C - R circuit at resonance, the statement which is not true is
View SolutionIn L−C−R series AC circuit,
View SolutionIn a series LCR circuit, at resonance, power factor is …….. .
View SolutionWhen current (I) in R-L series circuit becomes constant, where L is a pure inductor, which of the following given statements is/are correct?

View SolutionIn the circuit shown, L=1μH,C=1μFandR=1kΩ. They are connected in series with an source V=V0sinωt as shown. Which of the following options is/are correct ?
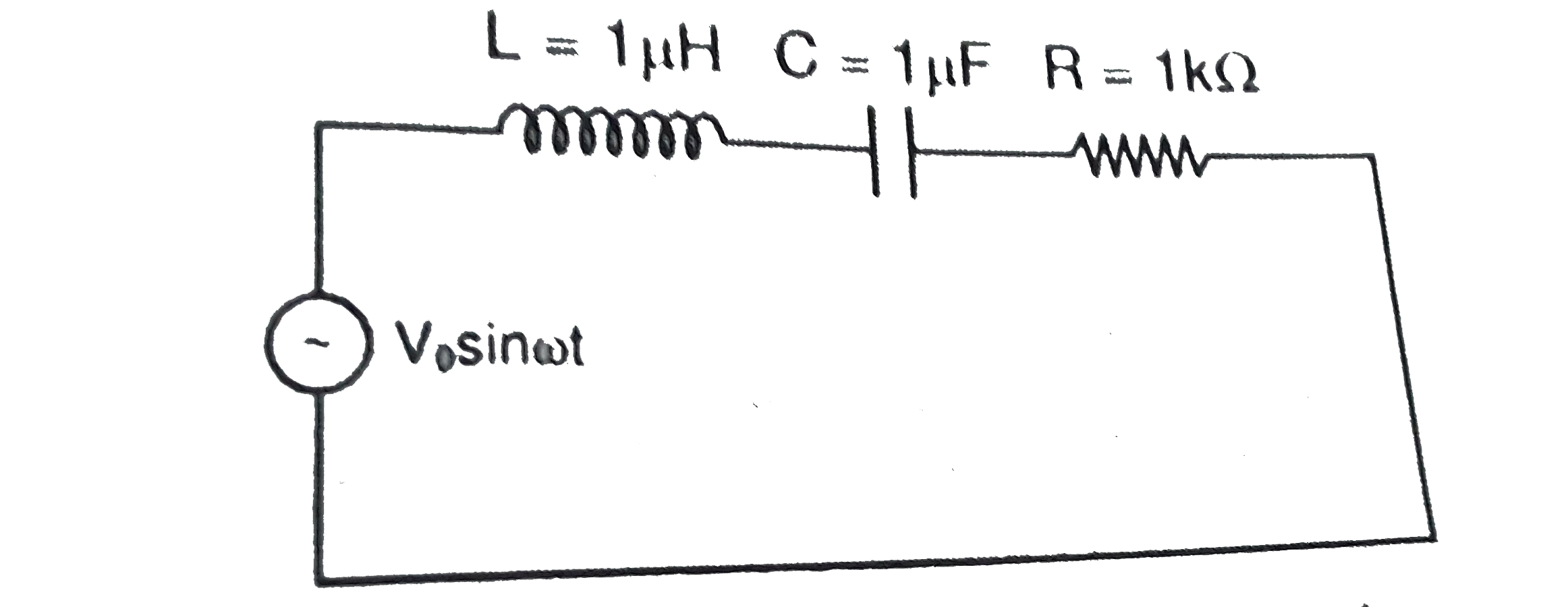
View Solution
