In a thermodynamic cyclic process ABC, internal energy at A is 10J and at B is 70J. Heat given in process B to C is 100J, then heat released or absorbed in process C to A is
760 J (absorbed)
760 J (released)
240 J (absorbed)
240 J (released)
To solve the problem step by step, we need to analyze the thermodynamic cyclic process ABC and apply the first law of thermodynamics.
Step 1: Understand the Given Information
- Internal energy at point A, UA=10J
- Internal energy at point B, UB=70J
- Heat given from B to C, QBC=100J
Step 2: Apply the First Law of Thermodynamics
The first law of thermodynamics states that the change in internal energy (ΔU) of a system is equal to the heat added to the system (Q) minus the work done by the system (W):
ΔU=Q−W
Step 3: Calculate the Change in Internal Energy from A to B
The change in internal energy from A to B is:
ΔUAB=UB−UA=70J−10J=60J
Step 4: Determine Heat Transfer from A to B
Using the first law for the process A to B:
ΔUAB=QAB−WAB
Rearranging gives:
QAB=ΔUAB+WAB
Since we do not have the work done, we will keep this equation for later reference.
Step 5: Calculate the Change in Internal Energy from B to C
The change in internal energy from B to C is:
ΔUBC=UC−UB
Using the first law for the process B to C:
ΔUBC=QBC−WBC
We do not know WBC yet, but we can express it as:
UC=UB+QBC−WBC
Step 6: Set Up the Equation for the Entire Cycle
In a cyclic process, the total change in internal energy over one complete cycle is zero:
ΔUCA+ΔUAB+ΔUBC=0
This implies:
ΔUCA=−(ΔUAB+ΔUBC)
Step 7: Substitute Known Values
We already calculated ΔUAB=60J and we need to find UC. We can express UC in terms of UB:
UC=UB+QBC−WBC
However, we can also express ΔUBC as:
ΔUBC=UC−UB=QBC−WBC
Now substituting into the cyclic equation:
ΔUCA=−(60+(UC−UB))
Step 8: Solve for QCA
We can express QCA in terms of the internal energies:
QCA=ΔUCA+WCA
Substituting ΔUCA=−(60+(UC−UB)):
QCA=−(60+(UC−70))+WCA
Step 9: Final Calculation
Using the cyclic condition:
0=QAB+QBC+QCA
Substituting known values:
0=QAB+100+QCA
Thus, we can find QCA if we find QAB.
Step 10: Conclusion
After solving the equations, we find that:
QCA=−760J
The negative sign indicates that heat is released during the process from C to A.
Final Answer
The heat released in the process from C to A is 760J.
---
- Internal energy at point A, UA=10J
- Internal energy at point B, UB=70J
- Heat given from B to C, QBC=100J
The first law of thermodynamics states that the change in internal energy (ΔU) of a system is equal to the heat added to the system (Q) minus the work done by the system (W):
ΔU=Q−W
The change in internal energy from A to B is:
ΔUAB=UB−UA=70J−10J=60J
Using the first law for the process A to B:
ΔUAB=QAB−WAB
Rearranging gives:
QAB=ΔUAB+WAB
Since we do not have the work done, we will keep this equation for later reference.
The change in internal energy from B to C is:
ΔUBC=UC−UB
Using the first law for the process B to C:
ΔUBC=QBC−WBC
We do not know WBC yet, but we can express it as:
UC=UB+QBC−WBC
In a cyclic process, the total change in internal energy over one complete cycle is zero:
ΔUCA+ΔUAB+ΔUBC=0
This implies:
ΔUCA=−(ΔUAB+ΔUBC)
We already calculated ΔUAB=60J and we need to find UC. We can express UC in terms of UB:
UC=UB+QBC−WBC
However, we can also express ΔUBC as:
ΔUBC=UC−UB=QBC−WBC
Now substituting into the cyclic equation:
ΔUCA=−(60+(UC−UB))
We can express QCA in terms of the internal energies:
QCA=ΔUCA+WCA
Substituting ΔUCA=−(60+(UC−UB)):
QCA=−(60+(UC−70))+WCA
Using the cyclic condition:
0=QAB+QBC+QCA
Substituting known values:
0=QAB+100+QCA
Thus, we can find QCA if we find QAB.
After solving the equations, we find that:
QCA=−760J
The negative sign indicates that heat is released during the process from C to A.
The heat released in the process from C to A is 760J.
Topper's Solved these Questions
Similar Questions
An ideal gas follows a cyclic process as shown in figure. Internal energy of gas at point A is 10 J while at B is 70 J. the heat absorbed by gas in BC is 120 J.
(a) How much heat is absorbed in process AB?
(b) Find heat energy rejected or absorbed by gas in process CA.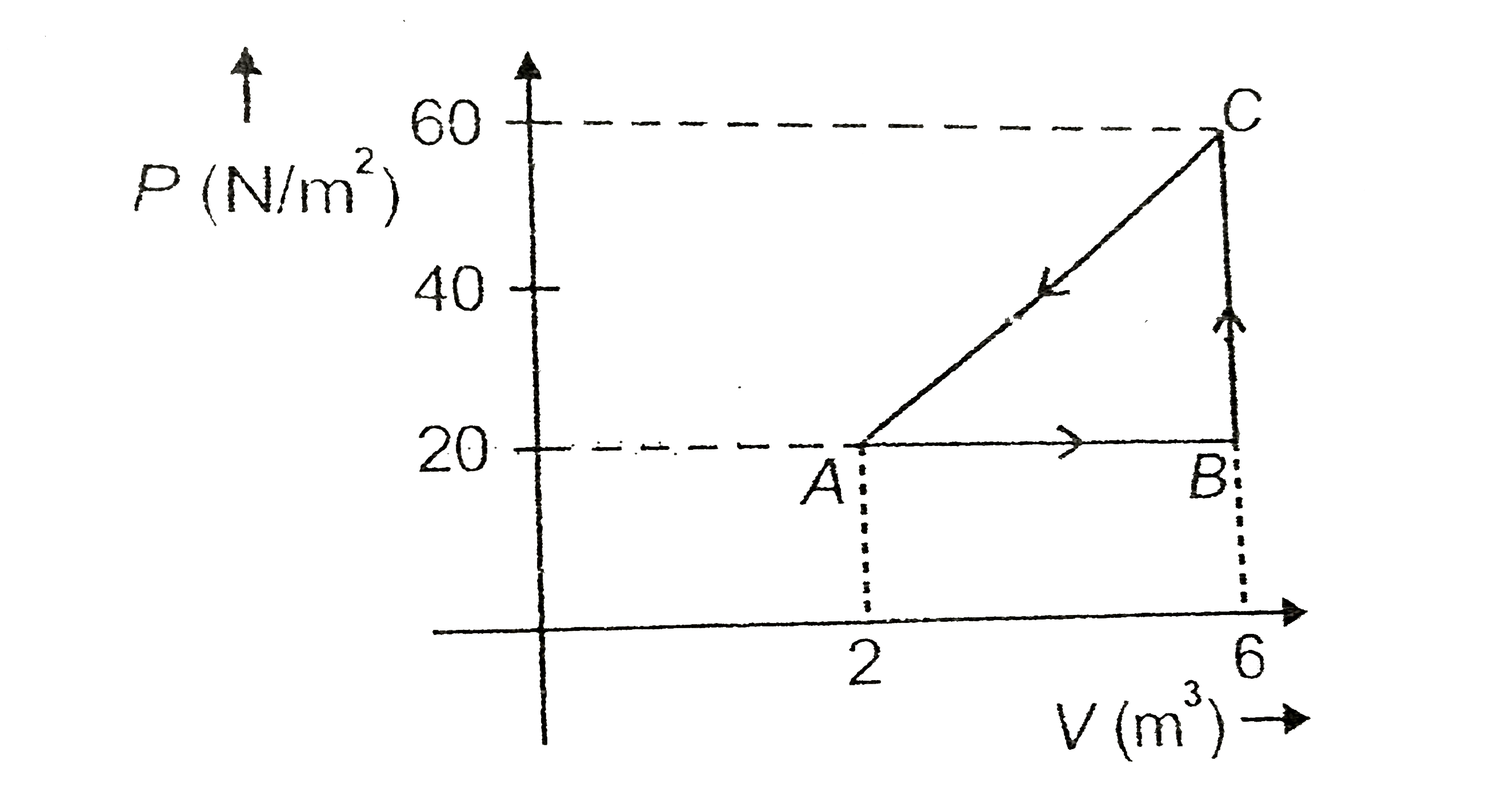
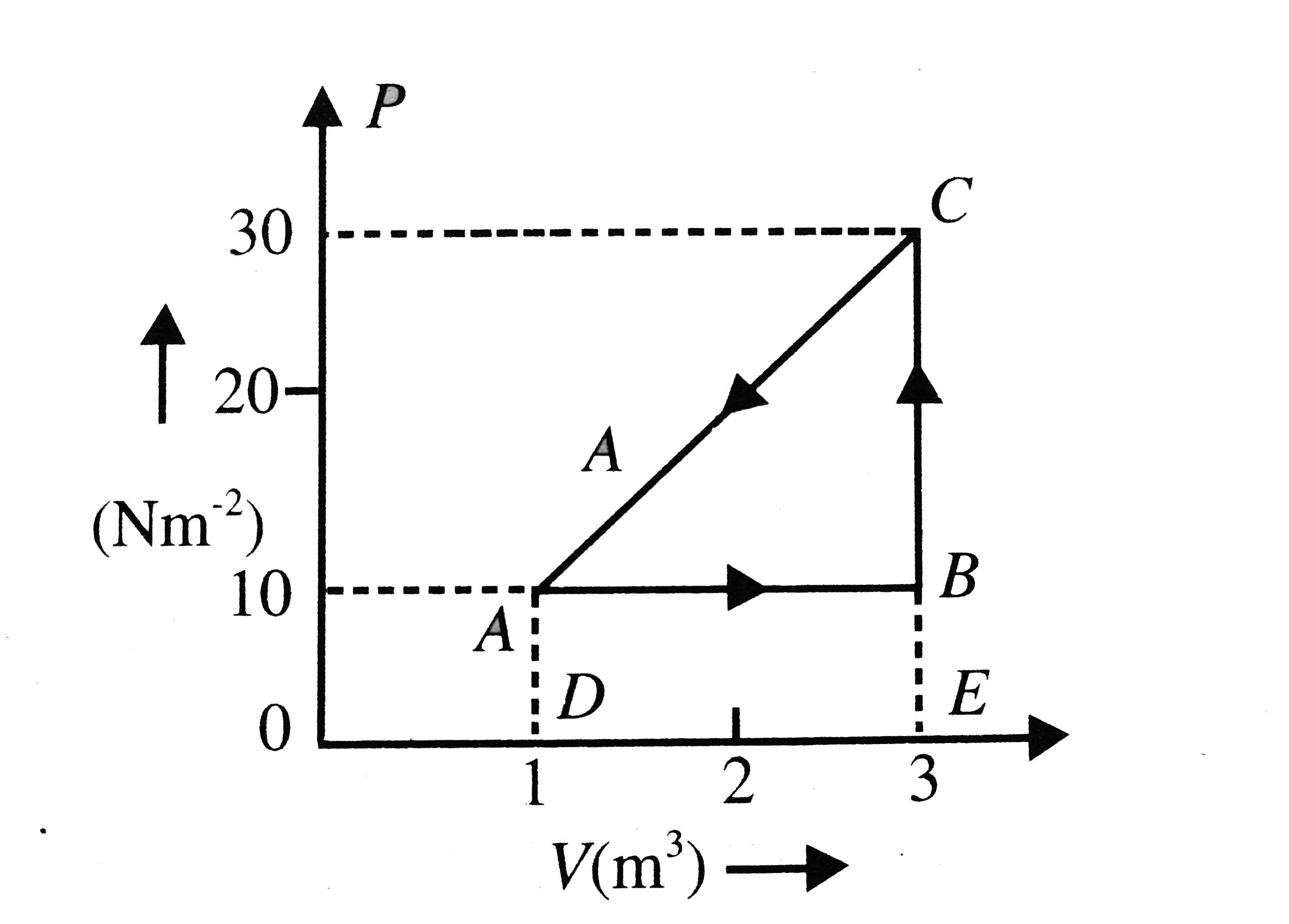
View SolutionAn ideal gas is taken round a cyclic thermodynamic process ABCA as shown if Fig. If the internal energy of the gas at point A is assumed zero while at B it is 50 J. The heat absorbed by the gas in the process BC is 90 J.
(a) What is the internal energy og the gas at point C ?
(b) How much heat energy is absorbed by the gas in the process AB?
(c ) Find the heat energy rejected or absorbed by the gas in the process CA.
(d) What is the net work done by the gas in the complete cycle ABCA ?
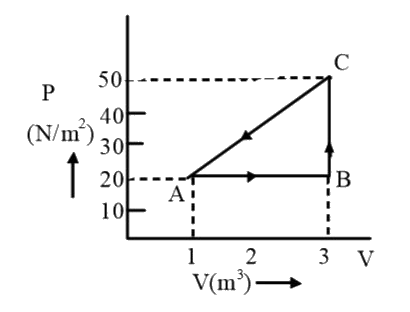
View SolutionIn the diagram, the graph between volume and pressure for a thermodynamical process in shown. If UA=0,UB=20J and the energy given from B to C is 30J, then at the stage of C, the internal energy of the system is –
View SolutionA gas is taken through a cyclic process ABCA as shown in, if 2.4 cal of heat is given in the process, what is the value of J ?
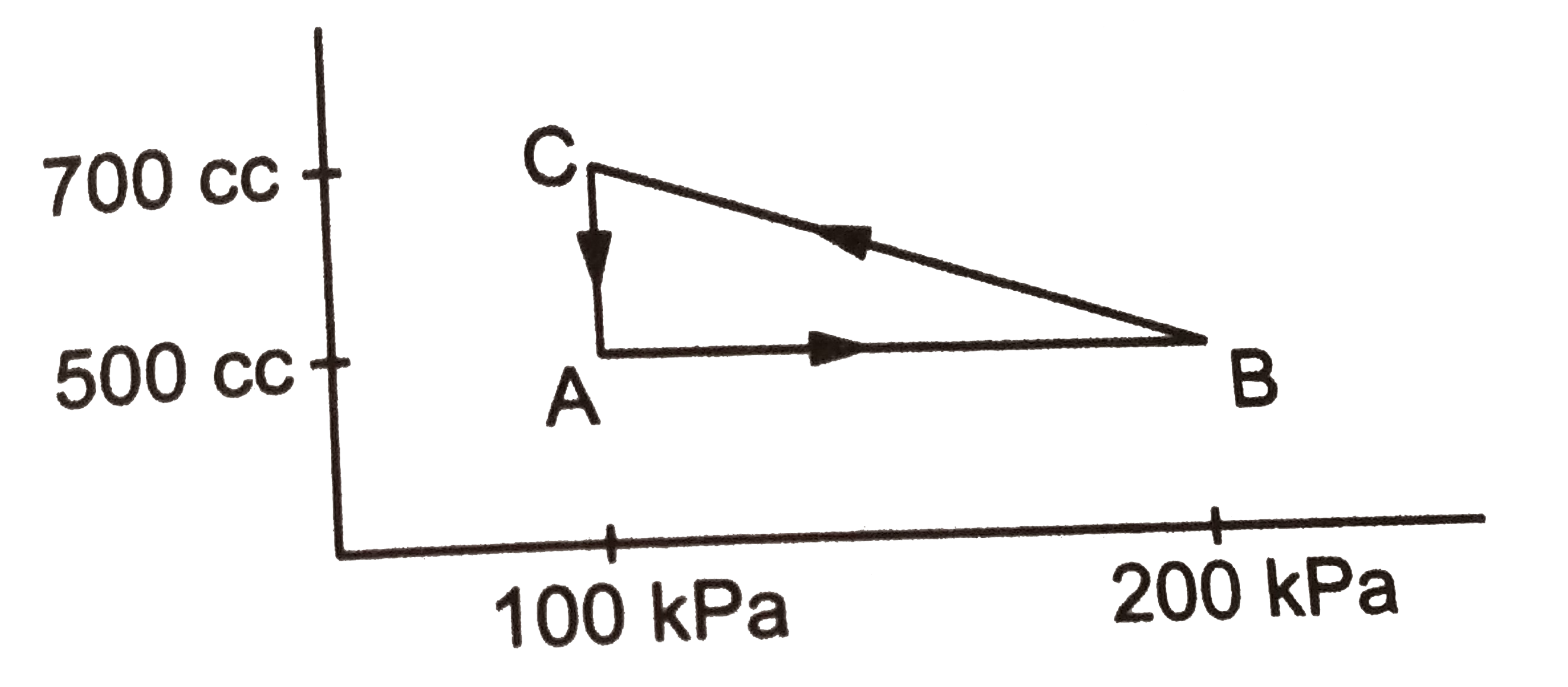
View SolutionA gas is taken through a cyclic process ABCA as shown in, if 2.4cal of heat is given in the process, what is the value of J ?

View SolutionIn (figure). shows two path that may be taken by a gas to go from a state A to state C
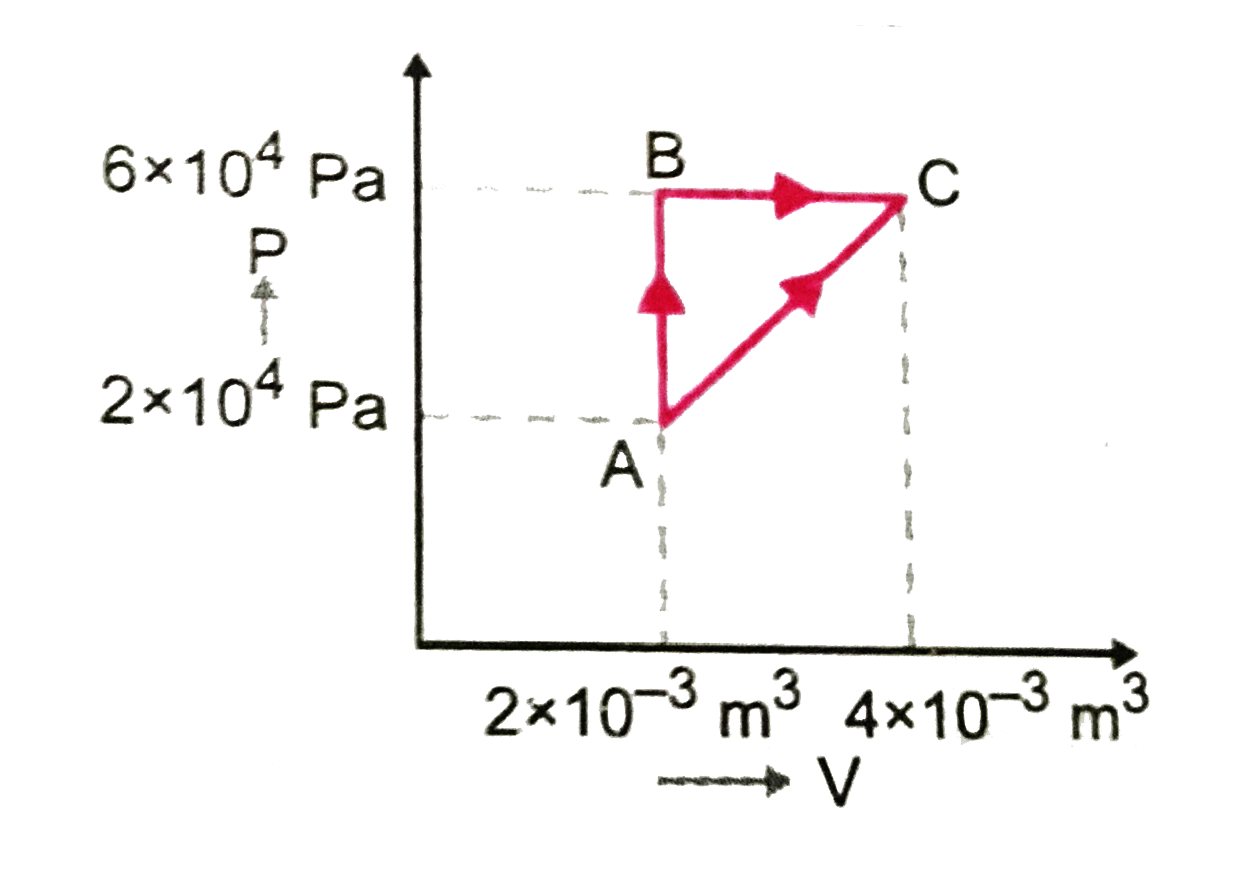
In the process AB, 400J of heat is added to the system and in process Bc, 100J of heat is added to the system. The heat absorbed by the system in the process AC will be
View SolutionIn the given graph, an ideal gas changes its state from A to C by two paths ABC and AC.
(a) Find the path along which work done is less.
(b) The internal energy of gas at A is 10J and the amount of heat supplied in path AC is 200J. Calculate the internal energy of gas at C.
(c) The internal energy of gas at state B is 20J. Find the amount of heat supplied to the gas to go from A to B.
View SolutionWhen a process is taken from process abc 100 J of heat is absorbed by system and 50 J of work is done by it. If work done in process adc is 60 J, then heat absorbed in this process
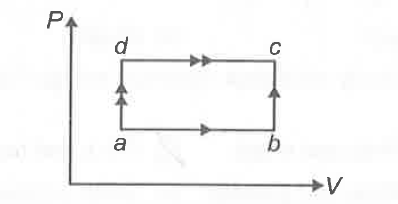
View SolutionIn a given process work done on a gas is 40 J and increase in its internal energy is 10J. Find heat given or taken to/from the gas in this process.
View SolutionIn a cyclic process shown in the figure an ideal gas is adiabatically taken from BtoA, the work done on the gas during the process BtoA is 30,J when the gas is taken from A to B the heat absorbed by the gas is 20J Then change in internal energy of the gas in the process A to B is :

View Solution
