When key K is open in a circuit as shown in figure, an ideal voltmeter reads 1.53 V. If key is closed then ideal ammeter reads 1A and voltmeter reads 1.03 V. Then EMF of cell and external resistance R are respectively
1.03 V, 1.53 Omega
1.53 V, 0.5 Omega
1.53 V, 1.03 Omega
1.03 V, 1.03 Omega
To solve the problem, we need to analyze the circuit behavior when the key K is open and closed. We will use the information given to find the EMF of the cell and the external resistance R.
1. Identify the Voltage When Key K is Open:
- When the key K is open, the voltmeter reads 1.53 V. This voltage is the EMF (E) of the cell because there is no current flowing in the circuit, and hence no voltage drop across any internal resistance.
- Therefore, we have:
E=1.53V
2. Identify the Voltage and Current When Key K is Closed:
- When the key K is closed, the voltmeter reads 1.03 V, and the ammeter reads 1 A. The voltage reading of 1.03 V is the voltage across the external resistance R.
- According to Ohm's law (V = IR), we can express the resistance R as:
V=I⋅R
- Substituting the known values:
1.03V=1A⋅R
- This simplifies to:
R=1.03Ω
3. Calculate the Internal Resistance (if needed):
- The EMF of the cell is given as 1.53 V when the key is open, and when the key is closed, the total voltage drop across the circuit (including internal resistance) is equal to the EMF.
- The voltage drop across the internal resistance (r) can be calculated as:
Voltage drop across internal resistance=E−V=1.53V−1.03V=0.50V
- Since the current is 1 A, we can find the internal resistance (r) using Ohm's law:
0.50V=1A⋅r⟹r=0.50Ω
4. Final Results:
- The EMF of the cell is:
E=1.53V
- The external resistance R is:
R=1.03Ω
Summary of Results:
- EMF of the cell (E) = 1.53 V
- External resistance (R) = 1.03 Ω
- When the key K is open, the voltmeter reads 1.53 V. This voltage is the EMF (E) of the cell because there is no current flowing in the circuit, and hence no voltage drop across any internal resistance.
- Therefore, we have:
E=1.53V
- When the key K is closed, the voltmeter reads 1.03 V, and the ammeter reads 1 A. The voltage reading of 1.03 V is the voltage across the external resistance R.
- According to Ohm's law (V = IR), we can express the resistance R as:
V=I⋅R
- Substituting the known values:
1.03V=1A⋅R
- This simplifies to:
R=1.03Ω
- The EMF of the cell is given as 1.53 V when the key is open, and when the key is closed, the total voltage drop across the circuit (including internal resistance) is equal to the EMF.
- The voltage drop across the internal resistance (r) can be calculated as:
Voltage drop across internal resistance=E−V=1.53V−1.03V=0.50V
- Since the current is 1 A, we can find the internal resistance (r) using Ohm's law:
0.50V=1A⋅r⟹r=0.50Ω
- The EMF of the cell is:
E=1.53V
- The external resistance R is:
R=1.03Ω
- EMF of the cell (E) = 1.53 V
- External resistance (R) = 1.03 Ω
Topper's Solved these Questions
Similar Questions
In the circuit shown in figure ammeter and voltmeter are ideal. If E=4V,R=9Ω and r=1Ω then readings of ammeter and voltmeter are
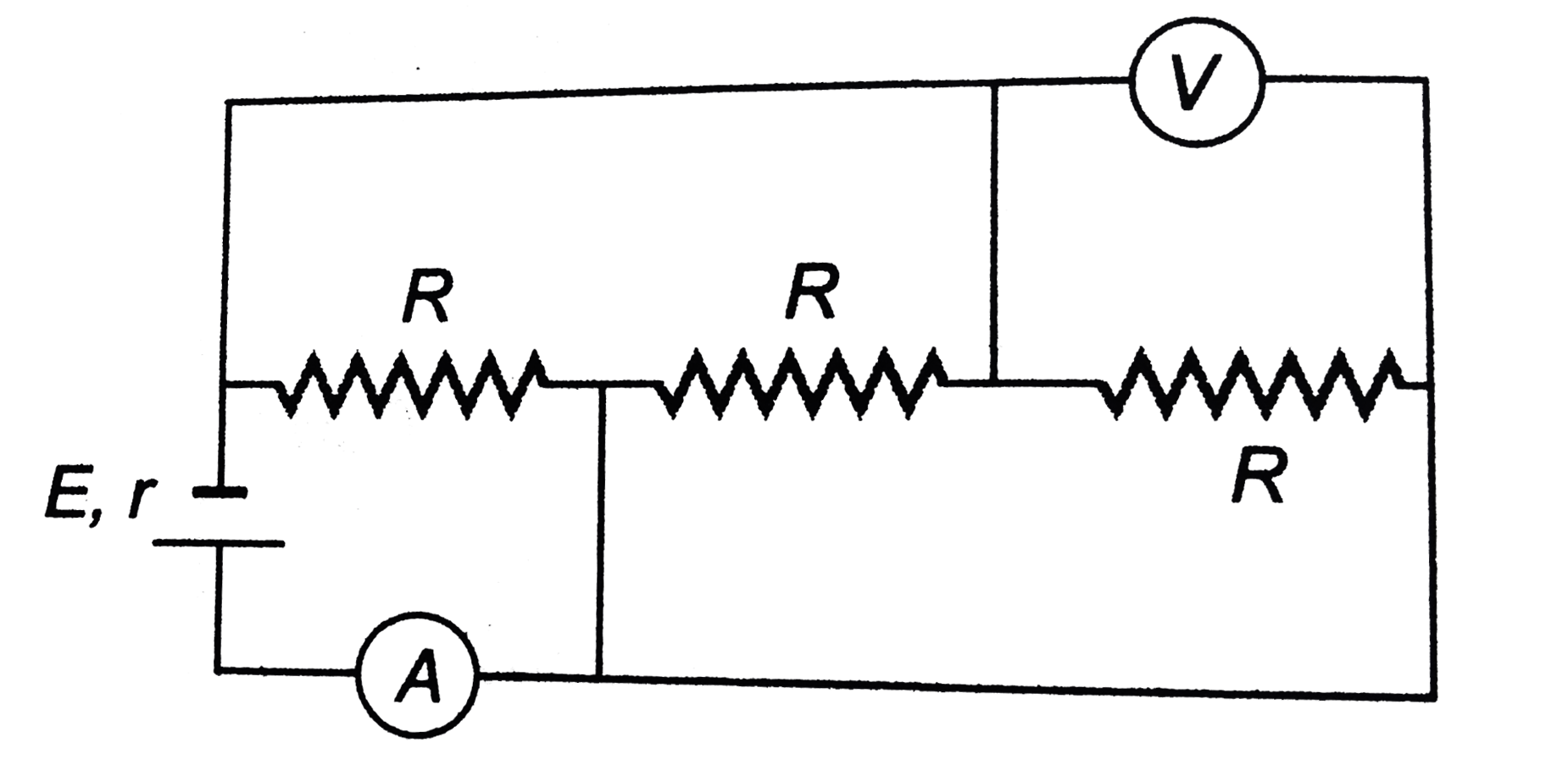
View SolutionIn the circuit shown in figure ammeter and voltmeter are ideal. If E=4V,R=9Ω and r=1Ω then readings of ammeter and voltmeter are

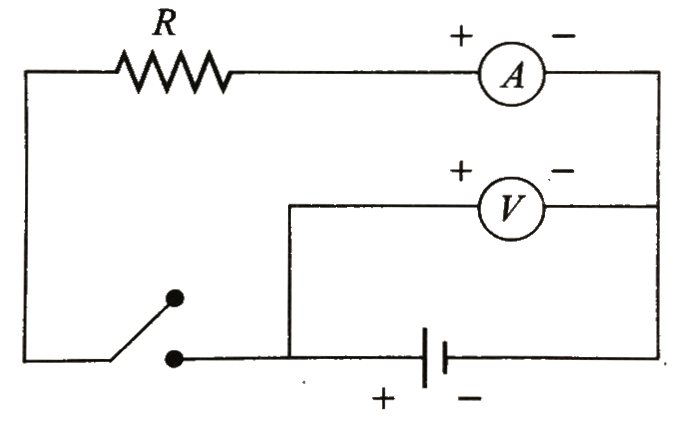
View SolutionIn the circuit shown in Fig. 6.50, an idel ammeter and an ideal voltmeter are used. Whan the key is open, the voltmeter reads 1.53V. When the key is closed, the ammeter reads 1.0A and the voltmeter reads 1.03V. The resistance R is
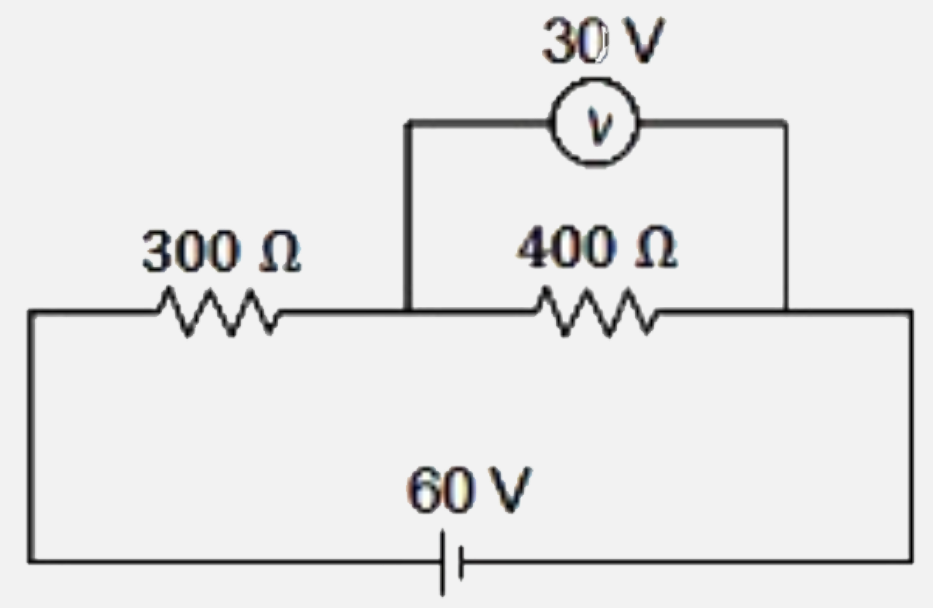
View SolutionIn the circuit figure, the voltmeter reads 30 V. The resistance of the voltmeter is
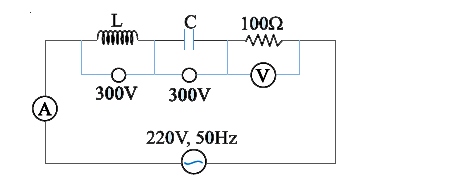
View SolutionIn the circuit shown in figure, what will be the readings of voltmeter and ammeter?
View SolutionIn the circuit shown below. The reading of the voltmeter V is
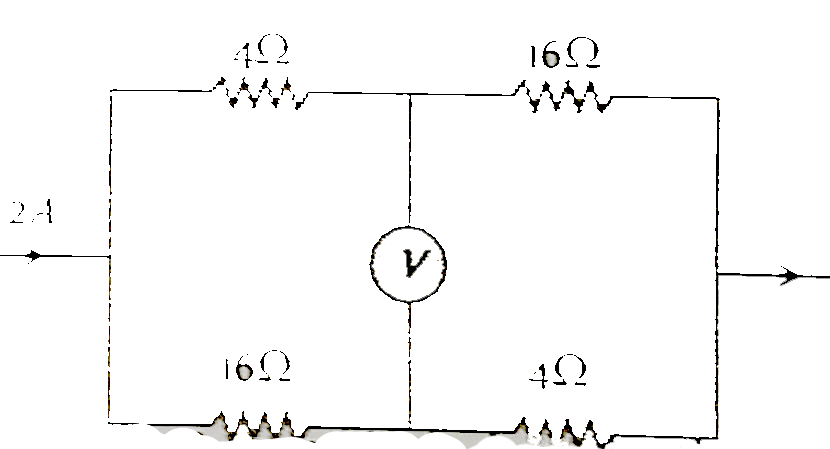
View SolutionConsider the circuit shown in the figure, the cell is ideal. The readings of the ideal voltmeters V1 and V2 in volts are respectively.

View SolutionAn ammeter and a voltmeter are connected in series to an ideal battery of emf E. If the ammeter reads I and voltmeter reading V, then
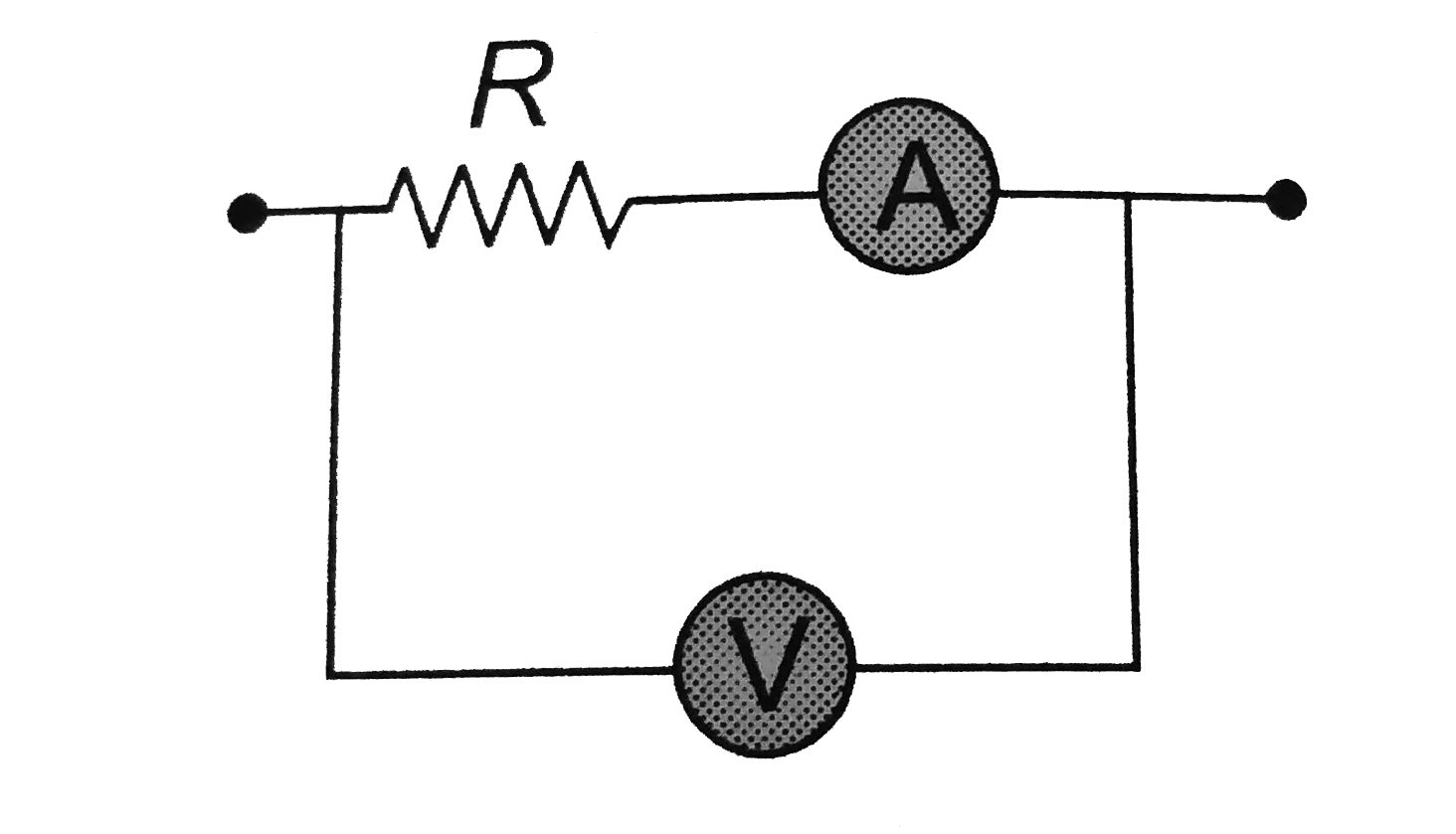
View SolutionIn the circuit shown the resistance of voltmeter is 10000ohm and that of ammeter is 20ohm. The ammeter reading is 0.10amp and voltmeter reading is 12 volts. Then R is equal to
View SolutionIn the circuit shown, A and V are ideal ammeter and voltmeter respectively. Reading of the voltmeter will be

View Solution
