Two metallic rods of same area of cross section, having lengths in ratio 2:3 and ratio of thermal conductivities 2:3 are connected in series across a temperature difference as shown in figure. The temperature of the junction (θ0) is
125°C
150°C
160°C
180°C
To solve the problem of finding the temperature of the junction (θ0) between two metallic rods connected in series, we can use the concept of thermal conductivity and the formula for heat transfer.
Given:
- Lengths of the rods are in the ratio 2:3.
- Thermal conductivities are in the ratio 2:3.
- Let the lengths of the rods be L1=2x and L2=3x.
- Let the thermal conductivities be k1=2y and k2=3y.
- Let the temperatures at the ends of the rods be T1 and T2.
1. Define the Heat Transfer Equation:
The rate of heat transfer Q through a rod can be expressed using Fourier's law of heat conduction:
Q=k⋅A⋅(T1−T2)L
where k is the thermal conductivity, A is the area of cross-section, T1 and T2 are the temperatures at the ends, and L is the length of the rod.
2. Set Up the Heat Transfer for Both Rods:
For rod 1:
Q=k1⋅A⋅(T1−θ0)L1
For rod 2:
Q=k2⋅A⋅(θ0−T2)L2
3. Equate the Heat Transfer:
Since the rods are in series, the heat transfer Q through both rods is the same:
k1⋅A⋅(T1−θ0)L1=k2⋅A⋅(θ0−T2)L2
4. Substitute the Values:
Substitute k1=2y, k2=3y, L1=2x, and L2=3x:
2y⋅A⋅(T1−θ0)2x=3y⋅A⋅(θ0−T2)3x
Simplifying this gives:
y⋅(T1−θ0)x=y⋅(θ0−T2)x
Canceling y and x (assuming they are non-zero):
T1−θ0=θ0−T2
5. Rearranging the Equation:
Rearranging gives:
T1+T2=2θ0
Thus, we can express θ0 as:
θ0=T1+T22
Conclusion:
The temperature of the junction (θ0) is the average of the temperatures at the ends of the rods:
θ0=T1+T22
- Lengths of the rods are in the ratio 2:3.
- Thermal conductivities are in the ratio 2:3.
- Let the lengths of the rods be L1=2x and L2=3x.
- Let the thermal conductivities be k1=2y and k2=3y.
- Let the temperatures at the ends of the rods be T1 and T2.
The rate of heat transfer Q through a rod can be expressed using Fourier's law of heat conduction:
Q=k⋅A⋅(T1−T2)L
where k is the thermal conductivity, A is the area of cross-section, T1 and T2 are the temperatures at the ends, and L is the length of the rod.
For rod 1:
Q=k1⋅A⋅(T1−θ0)L1
For rod 2:
Q=k2⋅A⋅(θ0−T2)L2
Since the rods are in series, the heat transfer Q through both rods is the same:
k1⋅A⋅(T1−θ0)L1=k2⋅A⋅(θ0−T2)L2
Substitute k1=2y, k2=3y, L1=2x, and L2=3x:
2y⋅A⋅(T1−θ0)2x=3y⋅A⋅(θ0−T2)3x
Simplifying this gives:
y⋅(T1−θ0)x=y⋅(θ0−T2)x
Canceling y and x (assuming they are non-zero):
T1−θ0=θ0−T2
Rearranging gives:
T1+T2=2θ0
Thus, we can express θ0 as:
θ0=T1+T22
The temperature of the junction (θ0) is the average of the temperatures at the ends of the rods:
θ0=T1+T22
Similar Questions
Two rods of similar area of cross section and length are joined as shown in the figure. The ratio of their thermal conductivity is 2:3. The free ends are maintained at 100∘C and 0∘C respectivley. THE temperature at junction in steady state is
 View Solution
View Solution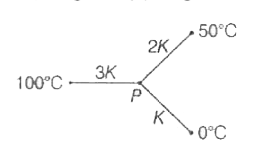
Three rods of the same dimension have thermal conductivity 3K , 2K and K. They are arranged as shown in the figure below
Then , the temperature of the junction in steady - state isView SolutionThe ratio of the areas of cross section of two rods of different materials is 1:2 and the ratio of ther themal conductivities of their mateirals is 4: 3. On keeping equal temperature difference between the ends of theserods, the rate of conduction of heat are equal. The ratio of the lengths of the rods is
View SolutionThree rods of same dimensions have thermal conductivity 3K,2K and K They are arranged as shown in Then the temperature of the junction in steady state is
 .View Solution
.View SolutionTwo identical rods are made of different materials whose thermal conductivities are K1andK2. They are placed end to end between two heat reservoirs at temperatures θ1andθ2. The temperature of the junction of the rod is
 View Solution
View SolutionFour identical heat conductors are connected as shown in the figure. The temperature θ of the junction is [rods are insulated from the sides ]
 View Solution
View SolutionFigure shown two adiabatic vessels, each containing a mass m of water at different temperature. The ends of a metal rod of length L, area of cross section A and thermal conductivity K, are inserted in the water as shown in the figure. Find the time taken for the difference between the temperature in the vessels to become half of the original value. The specific heat capacity of water is s. Neglect the heat capacity of the rod and the container and any loss of heat to the atmosphere.
 View Solution
View SolutionFour rods of same material and having the same cross section and length have been joined, as shown. The temperature of the junction of four rods will be :
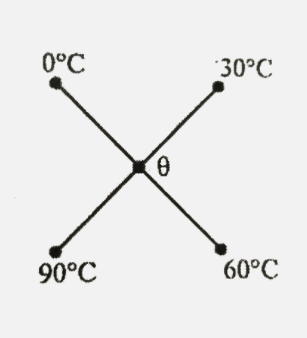 View Solution
View SolutionSteady state temperature are shown in the diagram. Find ratio of thermal conductivity k1k2 if length of all rods are same
 View Solution
View SolutionTwo rods of same length and areas of cross section A1 and A2 have their ends at same temperature. If K1 and K2 are their thermal conductivities, C1 and C2 their specific heats and ρ1 and ρ2 are their densities, then the condition that rate of flow of heat is same in both the rods is
View Solution

