Two resistances are joined in parallel whose resultant is 6/8ohm. One of the resistance wire is broken and the effective resistance becomes 2Ω . Then the resistance in ohm of the wire that got broken was
3/5
2
6/5
3
The correct Answer is:C
To solve the problem step by step, we will start by defining the variables and using the formulas related to resistances in parallel.
Step 1: Define the resistances
Let the two resistances be R1 and R2. According to the problem, they are connected in parallel.
Step 2: Use the formula for equivalent resistance in parallel
The formula for the equivalent resistance Req of two resistances in parallel is given by:
1Req=1R1+1R2
From the problem, we know that:
Req=68 ohm=0.75 ohm
Step 3: Rewrite the equation
Using the equivalent resistance formula:
10.75=1R1+1R2
This simplifies to:
43=1R1+1R2
Step 4: Assume one resistance is broken
When one of the resistances (let's assume R2) is broken, the effective resistance becomes R′eq=2 ohm. Therefore, we have:
R′eq=R1=2 ohm
Step 5: Substitute R1 into the equation
Now we can substitute R1 into the equation we derived earlier:
43=12+1R2
Step 6: Solve for R2
First, we need to express 1R2:
1R2=43−12
To subtract these fractions, we need a common denominator, which is 6:
43=86,12=36
Thus:
1R2=86−36=56
Now, taking the reciprocal gives:
R2=65 ohm
Step 7: Conclusion
The resistance of the wire that got broken is:
R2=1.2 ohm
Let the two resistances be R1 and R2. According to the problem, they are connected in parallel.
The formula for the equivalent resistance Req of two resistances in parallel is given by:
1Req=1R1+1R2
From the problem, we know that:
Req=68 ohm=0.75 ohm
Using the equivalent resistance formula:
10.75=1R1+1R2
This simplifies to:
43=1R1+1R2
When one of the resistances (let's assume R2) is broken, the effective resistance becomes R′eq=2 ohm. Therefore, we have:
R′eq=R1=2 ohm
Now we can substitute R1 into the equation we derived earlier:
43=12+1R2
First, we need to express 1R2:
1R2=43−12
To subtract these fractions, we need a common denominator, which is 6:
43=86,12=36
Thus:
1R2=86−36=56
Now, taking the reciprocal gives:
R2=65 ohm
The resistance of the wire that got broken is:
R2=1.2 ohm
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - B. Assertion and reason
18 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Match the columns
4 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Check point
70 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective
11 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrances gallery
25 Videos
Similar Questions
Two resistance wires on joining in parallel the resultant resistance is ohms 65 ohms. One of the wire breaks, the effective resistance is 2 ohms . The resistance of the broken wire is
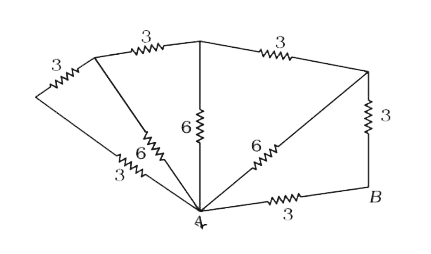
View SolutionAll resistance in the diagram are in ohm
Find the effective resistance (in ohm) between the points A and B
View SolutionWhat resistance must be connected to a 15 Ω resistance to provide an effective resistance of 6Ω ?
View SolutionAll resistances in fig. 5.34 are in ohm. Find the effective resistance between points A and B.

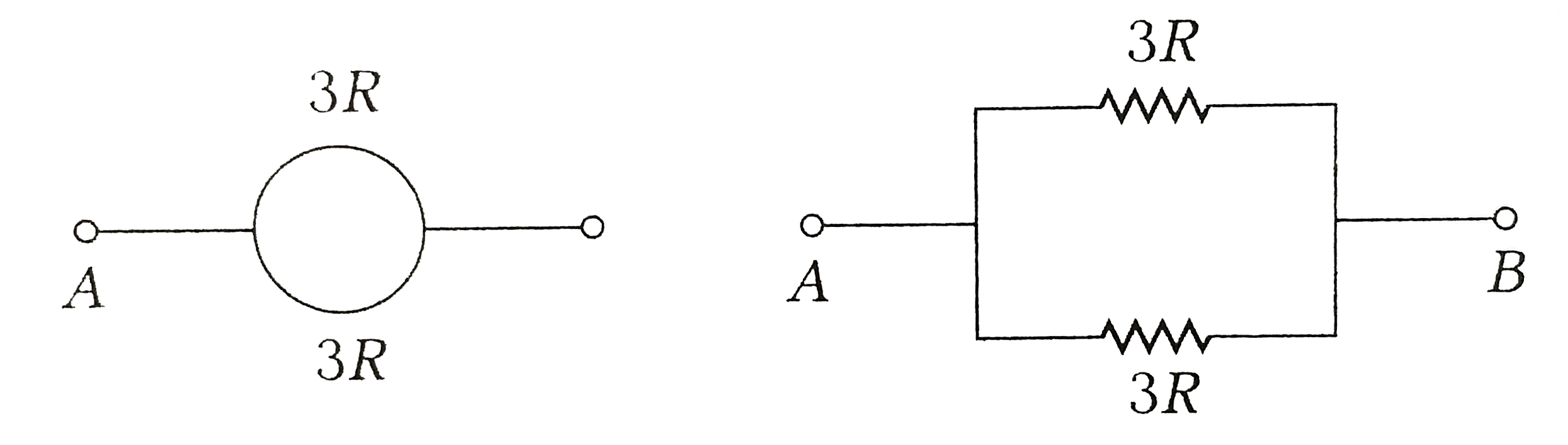
View SolutionA wire of resistance 6R is bent in the form of a circle. What is the effective resistance between the ends of the diameter?
View Solution"The resistance of a wire is 1 ohm". Explain the statement.
View SolutionResistance n, each of rohm, when connected in parallel give an equivalent resistance of Rohm. If these resistances were connected series, the combination would have a resistance in ohm, equal to
View SolutionA wire has resistance of 24Ω is bent in the following shape. The effective resistance between A and B is
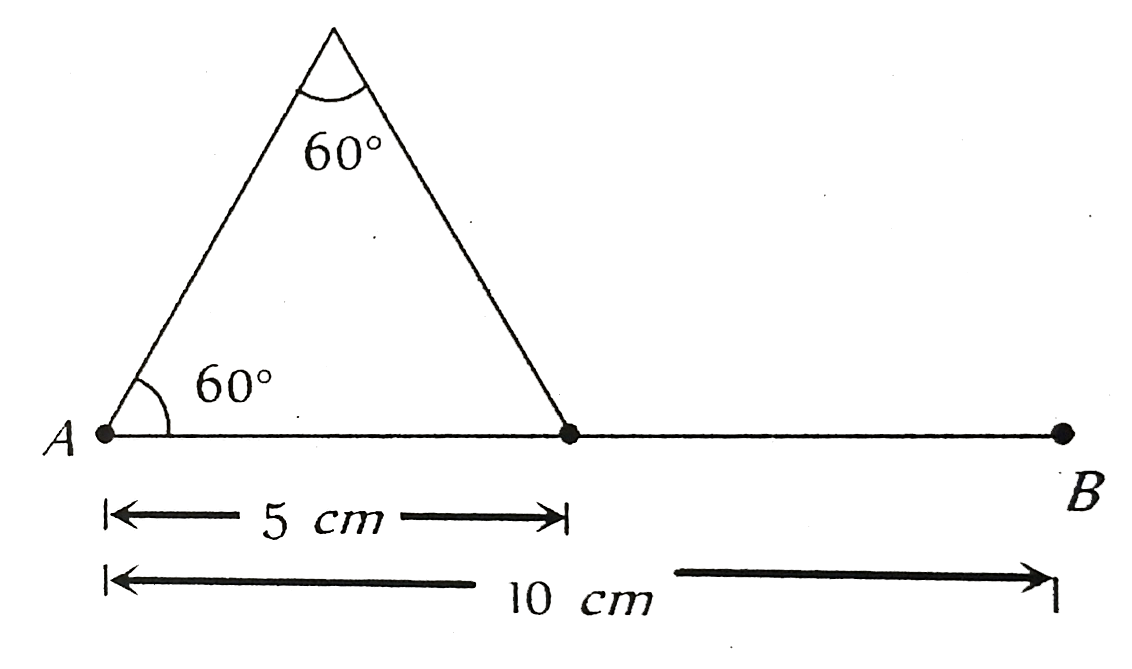
View SolutionA wire of resistance 8R is bent in the form of a circle. What is the effective resistance between the ends of a diameter AB?
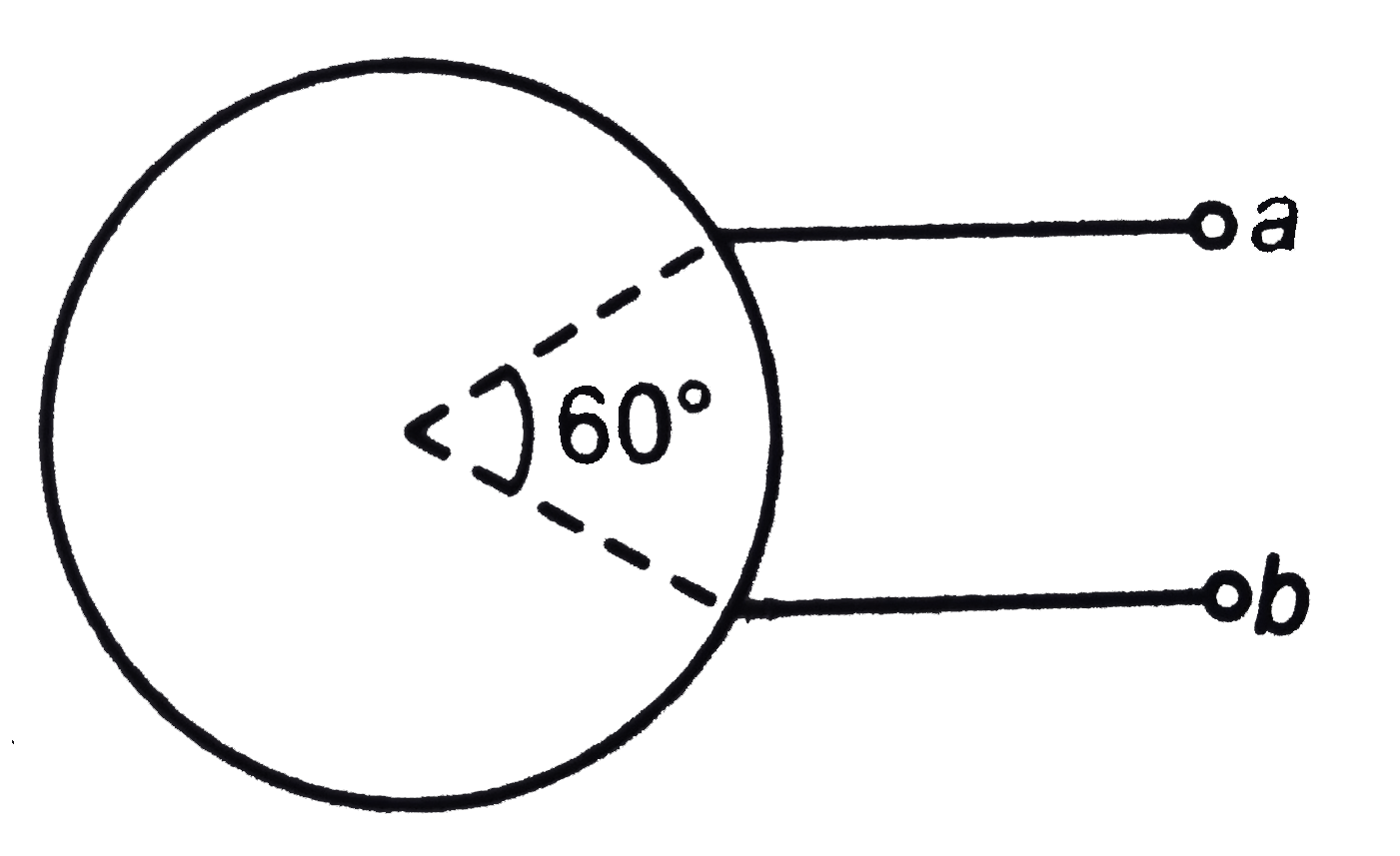
View SolutionA uniform wire of resistance 18Ω is bent in the form of a circle. The effective resistance across the points a and b is
View Solution