In ΔPQR,PQ=PR.A is a point in PQ and B is a point in PR , so that
QR = RA = AB = BP
show that :∠P:∠R=1:3
To solve the problem, we will follow these steps:
1. Identify the triangle and given information: We have triangle PQR where PQ = PR. A is a point on PQ and B is a point on PR such that QR = RA = AB = BP.
2. Establish that triangle PQR is isosceles: Since PQ = PR, triangle PQR is an isosceles triangle. Therefore, the angles opposite to the equal sides are also equal. Thus, we have:
∠Q=∠R
3. Set up the equal segments: According to the problem, we have:
QR=RA=AB=BP
Let's denote the common length of these segments as x. Therefore:
QR=RA=AB=BP=x
4. Consider triangle PAB: In triangle PAB, we have:
AB=PB
Since AB = BP = x, we can conclude that triangle PAB is also isosceles. Thus:
∠PAB=∠PBA
Let us denote these angles as ∠PAB=∠PBA=P.
5. Use the exterior angle theorem: In triangle PAB, the exterior angle ∠ABR can be expressed as the sum of the two opposite interior angles:
∠ABR=∠PAB+∠PBA=P+P=2P
6. Consider triangle ABR: In triangle ABR, since AB = AR (both equal to x), we have:
∠ABR=∠ARB
Let us denote these angles as ∠ABR=∠ARB=Q.
7. Sum of angles in triangle ABR: The sum of angles in triangle ABR is:
∠ABR+∠ARB+∠BAR=180∘
Substituting the known values:
2P+2Q=180∘
This simplifies to:
P+Q=90∘(1)
8. Consider angle RAQ: The angle RAQ can be expressed as:
∠RAQ=180∘−∠PAB−∠BAR=180∘−P−Q
Using equation (1):
∠RAQ=180∘−90∘=90∘
9. Consider triangle ARQ: In triangle ARQ, since AR = QR, we have:
∠QAR=∠QRA
Let’s denote these angles as R. Therefore:
R=3P
10. Final ratio of angles: In triangle PQR, we have:
∠P=Pand∠R=3P
Thus, the ratio of angles P to R is:
∠P∠R=P3P=13
Conclusion: Therefore, we have shown that:
∠P:∠R=1:3
∠Q=∠R
QR=RA=AB=BP
Let's denote the common length of these segments as x. Therefore:
QR=RA=AB=BP=x
AB=PB
Since AB = BP = x, we can conclude that triangle PAB is also isosceles. Thus:
∠PAB=∠PBA
Let us denote these angles as ∠PAB=∠PBA=P.
∠ABR=∠PAB+∠PBA=P+P=2P
∠ABR=∠ARB
Let us denote these angles as ∠ABR=∠ARB=Q.
∠ABR+∠ARB+∠BAR=180∘
Substituting the known values:
2P+2Q=180∘
This simplifies to:
P+Q=90∘(1)
∠RAQ=180∘−∠PAB−∠BAR=180∘−P−Q
Using equation (1):
∠RAQ=180∘−90∘=90∘
∠QAR=∠QRA
Let’s denote these angles as R. Therefore:
R=3P
∠P=Pand∠R=3P
Thus, the ratio of angles P to R is:
∠P∠R=P3P=13
∠P:∠R=1:3
Topper's Solved these Questions
- CHAPTERWISE REVISION (STAGE 1) BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 1) EXERCISE - Inequalities
5 Videos
- CHAPTERWISE REVISION (STAGE 1) BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 1) EXERCISE - Mid-point and intercept theorem
11 Videos
- CHAPTERWISE REVISION (STAGE 1) BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 1) EXERCISE - logrithms
20 Videos
- CHAPTER REVISION (STAGE 2) BOOK - ICSECHAPTER - CHAPTER REVISION (STAGE 2) EXERCISE - DISTANCE FORMULA
12 Videos
- CHAPTERWISE REVISION (STAGE 3) BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 3) EXERCISE - DISTANCE FORMULA
11 Videos
Similar Questions
In ΔPQR,PQ=PR.A is a point in PQ and B is a point in PR , so that
QR = RA = AB = BP
Find the vlaue of ∠Q.
View SolutionS is any point on side QR of a ΔPQR. Show that PQ+QR+RP>2PS .
View SolutionPQR is a triangle right-angled at P and M is a point on QR such that PM⊥QR. Show thatPM2=QM.MR.
View SolutionIf Q is a point on the side SR of a triangle ΔPSR such that PQ=PR then prove that PS>PQ
View SolutionIn a ΔPQR, N is a point on PR, such that QN⊥PR. If PN⋅NR=QN2, then prove that ∠PQR=90∘.
View SolutionIn quadrilateral PQRS , PS = QR and ∠SPQ=∠RQP . Prove that :
∠QPR=∠PQS
View SolutionIn figure A, B and C are points on OP, OQ and OR respectively such that AB || PQ and AC || PR. Show that BC || QR.
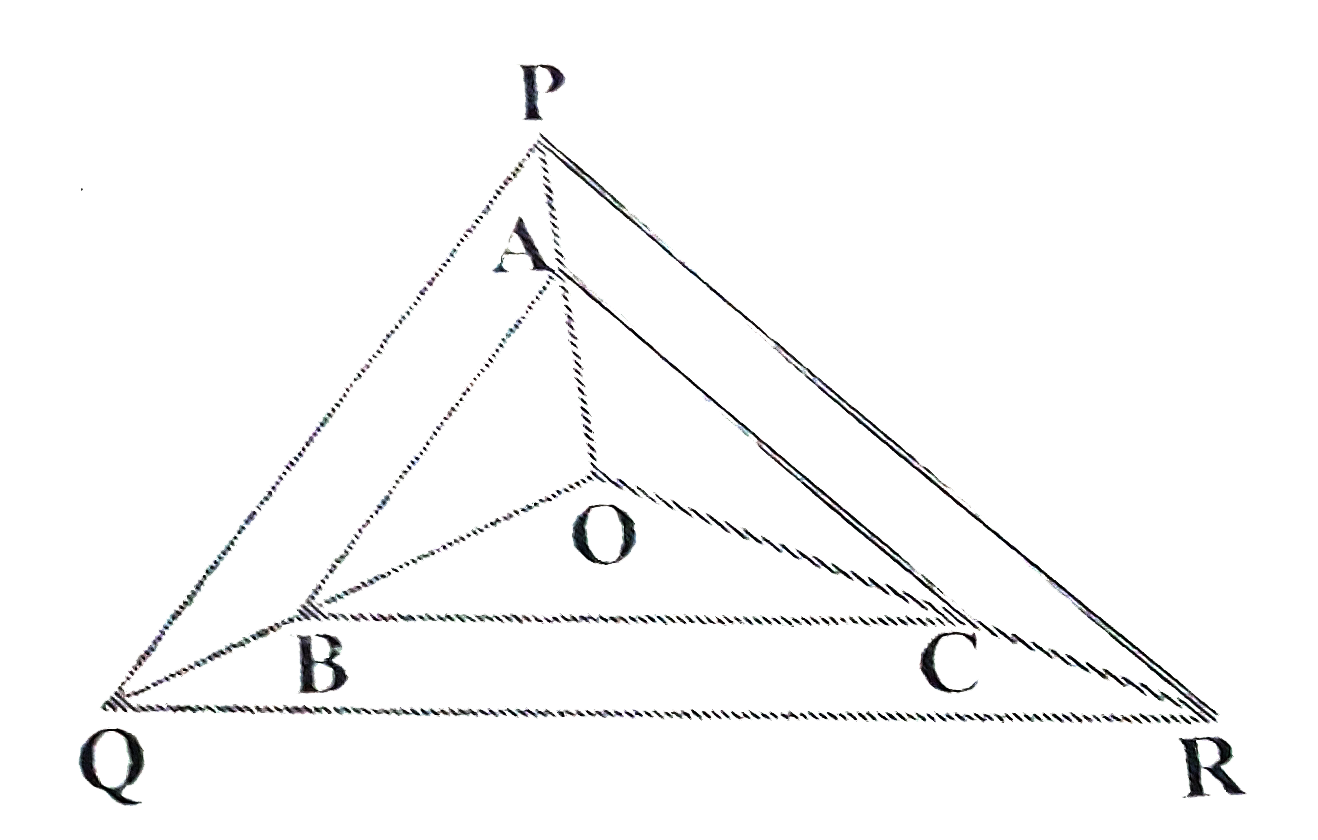
View SolutionS and T are points on sides PR and QR of ΔPQR such that ∠P=∠RTS Show that ΔRPQ~ΔRTS
View SolutionIn Figure, PQR is a triangle and S is any point in its interior, show that SQ+SR<PQ+PR. Given : S is any point in the interior of PQR To Prove : SQ+SR<PQ+PR Construction: Produce QS to meet PR in T
View SolutionIn ΔPQR,Pq=PR and S is the mid-point of PQ. A line drawn from S parallel to QR, intersects the line PR at T. Prove that PS = PT.
View Solution
