In quadrilateral PQRS , PS = QR and ∠SPQ=∠RQP . Prove that :
∠QPR=∠PQS
Step by step video & image solution for In quadrilateral PQRS , PS = QR and angle SPQ = angle RQP . Prove that : angle QPR = angle PQS by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CHAPTERWISE REVISION (STAGE 3) BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 3) EXERCISE - ISOSCELES TRIANGLES
2 Videos
- CHAPTERWISE REVISION (STAGE 3) BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 3) EXERCISE - INEQUALITIES
7 Videos
- CHAPTERWISE REVISION (STAGE 3) BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 3) EXERCISE - LOGARITHM
9 Videos
- CHAPTERWISE REVISION (STAGE 1) BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 1) EXERCISE - Graphical solution
10 Videos
- CIRCLEBOOK - ICSECHAPTER - CIRCLEEXERCISE - EXERCISE 17(D)
12 Videos
Similar Questions
In quadrilateral PQRS , PS = QR and ∠SPQ=∠RQP . Prove that :
PR=QS
View SolutionIn a quadrilateral ABCD, AB = CD and ∠B=∠C. Prove that
AC=AB
View SolutionIn a quadrilateral ABCD, AB = CD and ∠B=∠C. Prove that
AD is parallel to BC.
View SolutionThe given figure shows PQ=PRand∠Q=∠R.
Prove that ΔPQS=ΔPRT
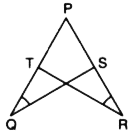
View SolutionIn quadrilateral ABCD, AD = BC and BD = CA. Prove that :
(i) ∠ADB=∠BCA
(ii) ∠DAB=∠CBA
View SolutionIn ΔPQR, If ∠R>∠Q, then
View SolutionIn quadrilateral PQRS, ∠P:∠Q:∠R:∠S=3:4:6:7. Calculate each angle of the quadrilateral and then prove that PQ and SR are parallel to each other.
(i) Is PS also parallel to QR ?
(ii) Assign a special name to quadrilateral PQRS.
View SolutionIn the adjoining figure PQ = PR and ∠PRQ=70∘ Find ∠QPR.
View SolutionThe sides PQ, PR of triangle PQR are equal, and S, T are points on PR, PQ such that ∠PSQand∠PTR are right angles
Prove that the triangles PTR and PSQ are congruent.
View SolutionWhich of the following pairs of triangles are congruent ? In each case, state the condition of congruency :
(a) In ΔABCandΔDEF, AB = DE, BC = EF and ∠B=∠E.
(b) In ΔABCandΔDEF,∠B=∠E=90∘, AC = DF and BC = EF.
(c) In ΔABCandΔQRP, AB = QR, ∠B=∠Rand∠C=∠P.
(d) In ΔABCandΔPQR, AB = PQ, AC = PR and BC = QR.
(e) In ΔABCandΔPQR, BC = QR, ∠A=90∘,∠C=∠R=40∘and∠Q=50∘.
View Solution
