In a ΔPQR, N is a point on PR, such that QN⊥PR. If PN⋅NR=QN2, then prove that ∠PQR=90∘.
To prove that ∠PQR=90∘ given that PN⋅NR=QN2 in triangle PQR with N being a point on PR such that QN⊥PR, we can follow these steps:
Step 1: Understand the Given Information
We have triangle PQR with point N on line segment PR such that QN is perpendicular to PR. We are given that PN⋅NR=QN2.
Step 2: Set Up the Angles
Let ∠PQR=x and ∠QRP=y. Therefore, ∠QPR=180∘−(x+y).
Step 3: Use the Given Condition
From the given condition PN⋅NR=QN2, we can rewrite this in terms of ratios:
PNQN=QNNR
This implies that triangles PNQ and NRQ are similar by the property of proportional sides.
Step 4: Establish Corresponding Angles
Since triangles PNQ and NRQ are similar, we can conclude that:
∠PNQ=∠NRQ
Let ∠PNQ=α and ∠NRQ=α.
Step 5: Relate Angles in Triangle PQR
In triangle PQR:
- ∠PQR=x
- ∠QRP=y
- ∠QPR=180∘−(x+y)
From the similarity, we have:
∠PQN=∠QNR=90∘−α
Step 6: Sum of Angles in Triangle PQR
Using the angles we have:
∠PQR+∠QRP+∠QPR=180∘
Substituting the angles:
x+y+(90∘−(x+y))=180∘
This simplifies to:
90∘=90∘
This confirms our angle relationships hold true.
Step 7: Conclude that ∠PQR=90∘
Since we have established that the angles satisfy the triangle angle sum property, we can conclude:
∠PQR=90∘
Final Conclusion
Thus, we have proven that ∠PQR=90∘.
---
We have triangle PQR with point N on line segment PR such that QN is perpendicular to PR. We are given that PN⋅NR=QN2.
Let ∠PQR=x and ∠QRP=y. Therefore, ∠QPR=180∘−(x+y).
From the given condition PN⋅NR=QN2, we can rewrite this in terms of ratios:
PNQN=QNNR
This implies that triangles PNQ and NRQ are similar by the property of proportional sides.
Since triangles PNQ and NRQ are similar, we can conclude that:
∠PNQ=∠NRQ
Let ∠PNQ=α and ∠NRQ=α.
In triangle PQR:
- ∠PQR=x
- ∠QRP=y
- ∠QPR=180∘−(x+y)
∠PQN=∠QNR=90∘−α
Using the angles we have:
∠PQR+∠QRP+∠QPR=180∘
Substituting the angles:
x+y+(90∘−(x+y))=180∘
This simplifies to:
90∘=90∘
This confirms our angle relationships hold true.
Since we have established that the angles satisfy the triangle angle sum property, we can conclude:
∠PQR=90∘
Thus, we have proven that ∠PQR=90∘.
Topper's Solved these Questions
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - TRIANGLESEXERCISE - Long Answer Type Questions18videos
TRIANGLES
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - TRIANGLESEXERCISE - Very Short Answer Typw Questions12videos
TRIANGLES
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - LONG ANSWER TYPE QUESTIONS20videos
SURFACE AREAS AND VOLUMES
Similar Questions
In a triangle ABC , N is a point on AC such that BN⊥AC . If BN2=ANNC , prove that ∠B=90o .
View SolutionIf Q is a point on the side SR of a triangle ΔPSR such that PQ=PR then prove that PS>PQ
View SolutionIi ΔPQR, PD⊥QR such that D lies on QR, if PQ=a,PR=b,QD=c and DR=d, then prove that (a+b)(a-b)=(c+d)(c-d).
View SolutionIn ΔPQR,PQ=PR.A is a point in PQ and B is a point in PR , so that
QR = RA = AB = BP
show that :∠P:∠R=1:3View SolutionIn ΔPQR,PQ=PR.A is a point in PQ and B is a point in PR , so that
QR = RA = AB = BP
Find the vlaue of ∠Q.View SolutionIn a triangle PQR, L and M are two points on the base QR, such that ∠LPQ=∠QRP and ∠RPM=∠RQP. Prove that:
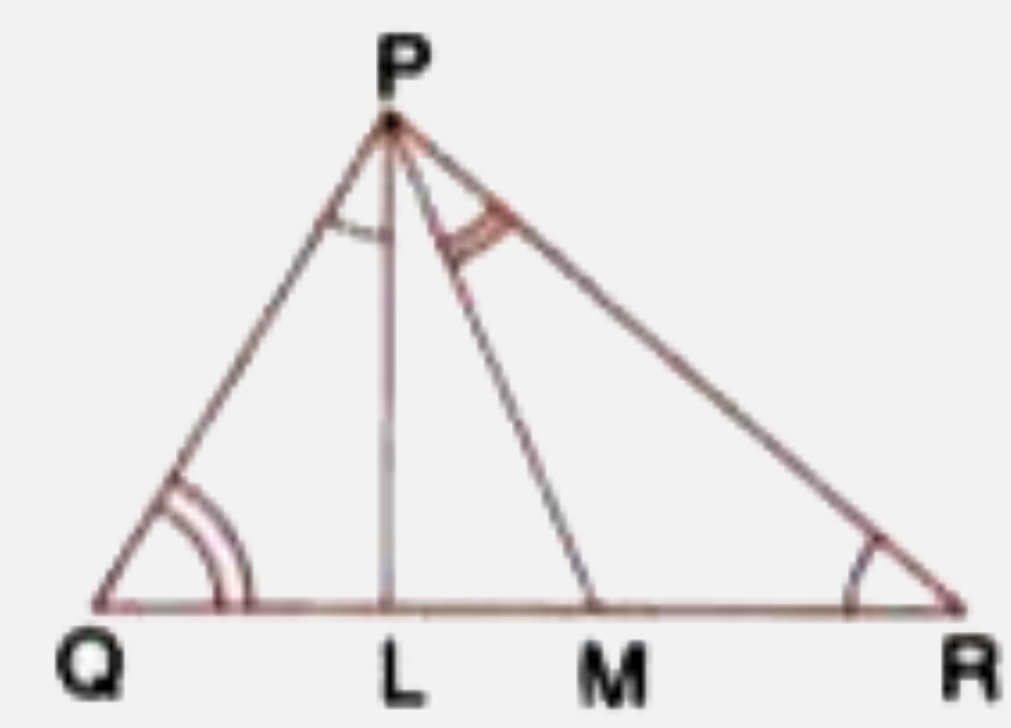
ΔPQL~ΔRPMView SolutionThe sides PQ, PR of triangle PQR are equal, and S, T are points on PR, PQ such that ∠PSQand∠PTR are right angles
Prove that the triangles PTR and PSQ are congruent.View SolutionA Δ ABC is right angled at A. L is a point on BC such that AL⊥ BC. Prove that ∠BAL=∠ACB.
View SolutionIf S is the mid-point of side QR of a ΔPQR, then prove that PQ+PR=2PS.
View SolutionA ΔABC is right angled at A. L is a point on BC such that AL⊥ BC. Prove that ∠BAL=∠ACB.
View Solution

