In the given figure, ΔABC and ΔAMP are right angled at B and M respectively.
Given AC=10cm,AP=15cmandPM=12cm.
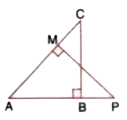
Prove that : ΔABC−ΔAMP
Step by step video & image solution for In the given figure, DeltaABC and DeltaAMP are right angled at B and M respectively. Given AC = 10 cm, AP = 15 cm and PM = 12 cm. Prove that : DeltaABC - DeltaAMP by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)BOOK - ICSECHAPTER - SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)EXERCISE - EXERCISE 15(B)
17 Videos
- SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)BOOK - ICSECHAPTER - SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)EXERCISE - EXERCISE 15(C)
24 Videos
- SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)BOOK - ICSECHAPTER - SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)EXERCISE - EXERCISE 15(E)
61 Videos
- SIMILARITY BOOK - ICSECHAPTER - SIMILARITY EXERCISE - MULTIPLE CHOICE QUESTIONS (COMPETENCY BASED QUESTIONS)
10 Videos
- SOLVING (SIMPLE) PROBLEMS (BASED ON QUADRATIC EQUATIONS)BOOK - ICSECHAPTER - SOLVING (SIMPLE) PROBLEMS (BASED ON QUADRATIC EQUATIONS)EXERCISE - Exercise 6(e )
18 Videos
Similar Questions
In the given figure, ΔABC and ΔAMP are right angled at B and M respectively.
Given AC=10cm,AP=15cmandPM=12cm.
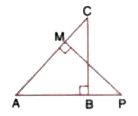
Find : AB and BC.
View SolutionIn the given figure ΔABCandΔAMP are right angled at B and M respectively.
Given AC = 10 cm, AP = 15 cm and PM = 12 cm.
(i) Prove ΔABC~ΔAMP.
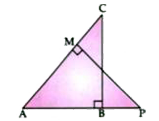
View SolutionIn ΔABC,∠ABC=∠DAC, AB = 8 cm, AC = 4 cm and AD = 5 cm.
(i) Prove that ΔACD~ΔBCA.
View SolutionIn ΔABC,∠ABC=∠DAC,AB=8cm,AC=4cmandAD=5cm.

Prove that ΔACD is similar to ΔBCA.
View SolutionConstruct a ΔABC right angled at B in which BC = 6.0 cm and AC = 8.0 cm.
View SolutionIn the given figure , ABC is a right triangle, right angled at B. Medians AD and CE are of respective length 5 cm and 2√5cm . Find the length of AC.

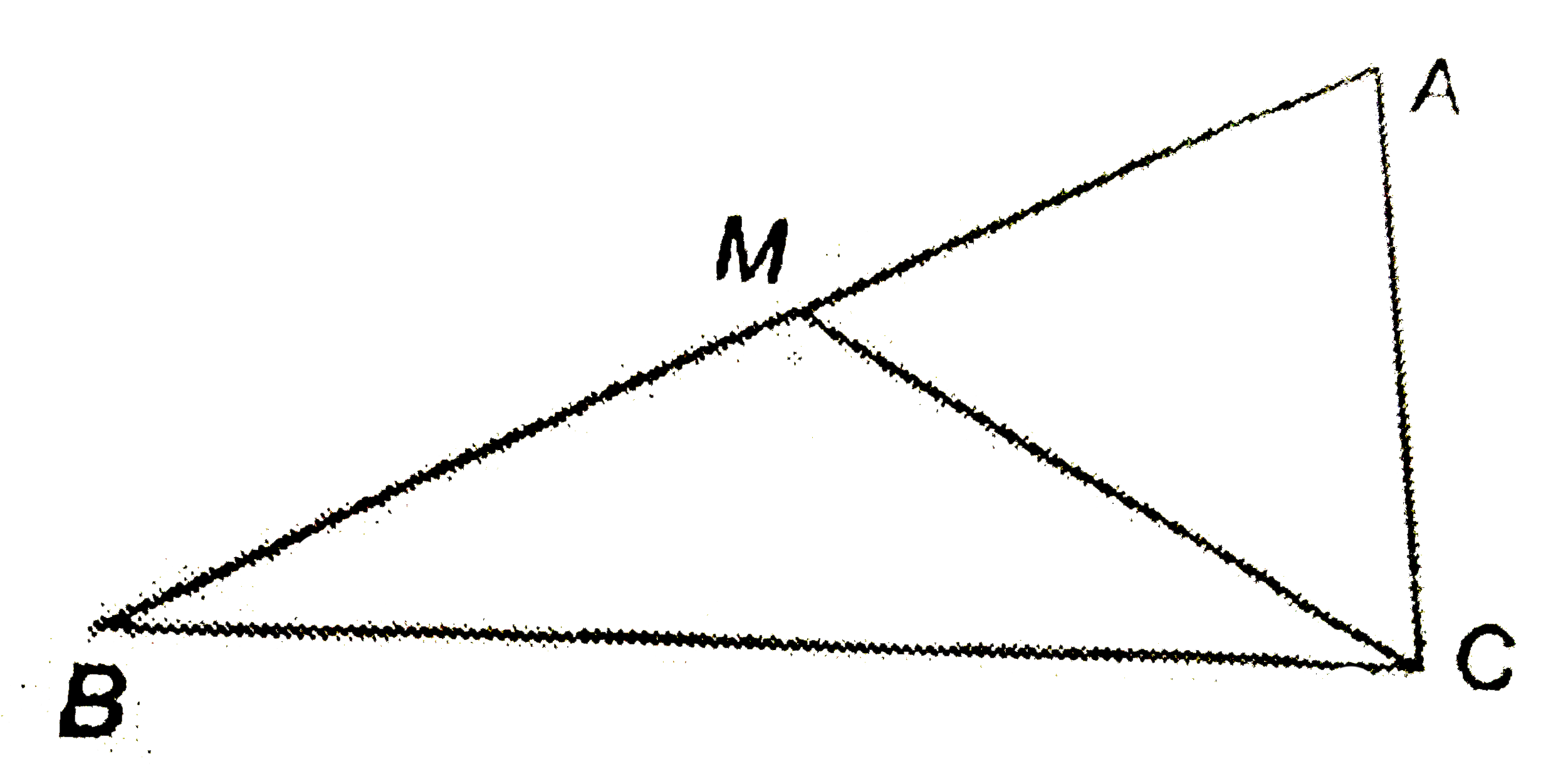
View SolutionIn the adjoining figure, ΔABC is right angled at C and M is the mid-point of hypotenuse AB, If AC = 32 cm and BC = 60 cm, then find the length of CM.
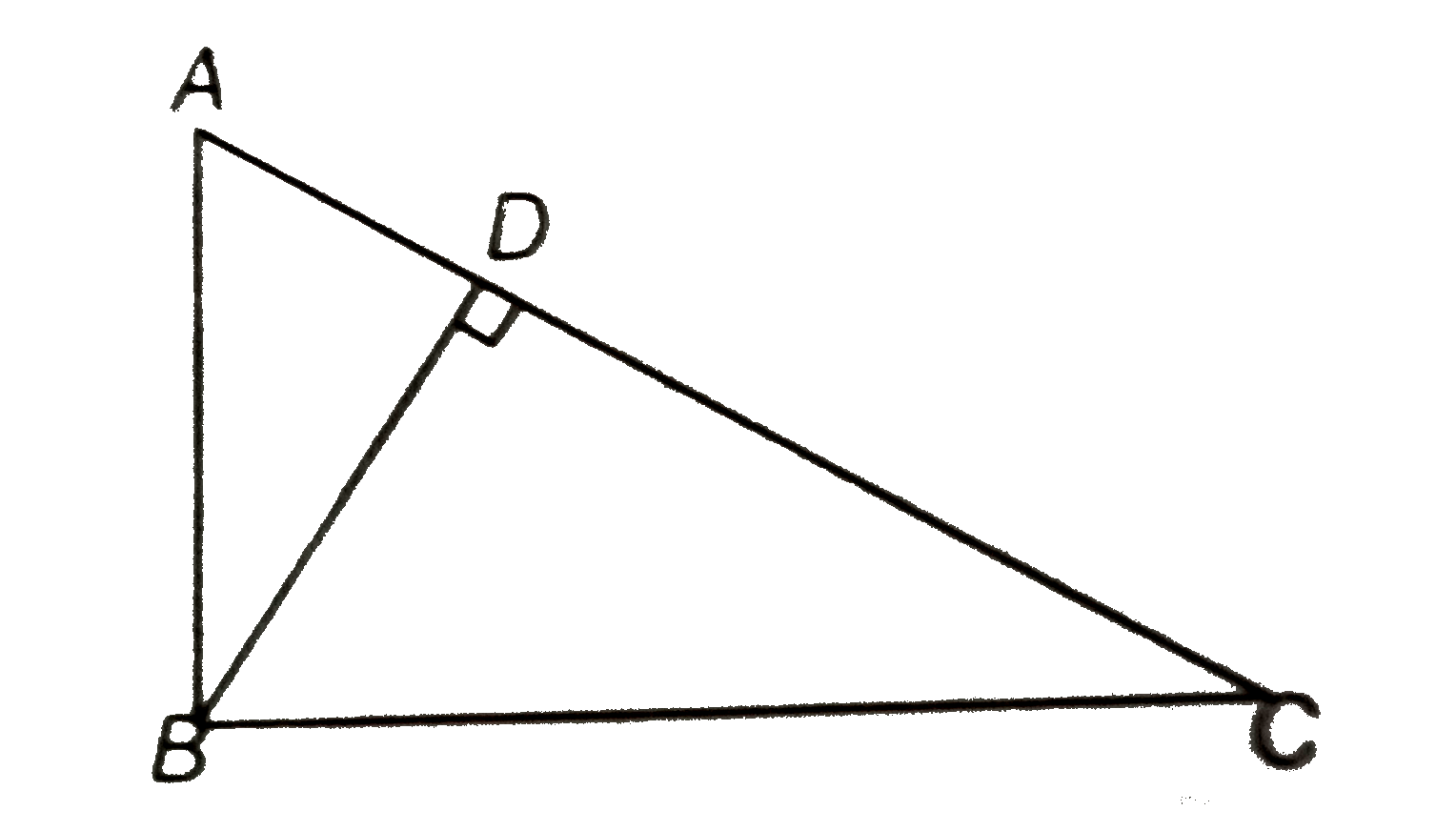
View SolutionIn given figure, ABC is a triangle right angled at B and BD⊥AC. If AD=4 cm and CD= 5 cm, then find BD and AB.
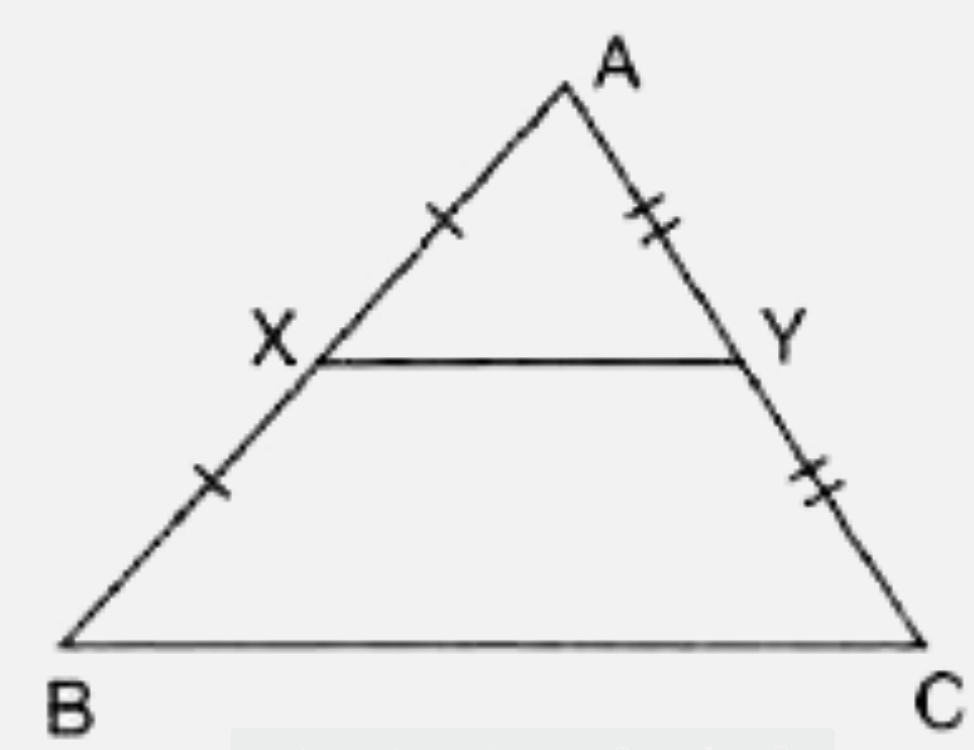
View SolutionIn the figure, given below X and Y are the mid-points of AB and AC respectively. Given that BC = 6 cm, AB = 5-4 cm and AC = 5-0 cm, calculate the perimeter of trapezium YXBC.
View SolutionConstruct a right angled ΔABC, right angled at A if hypotenuse BC = 5 cm and side AB = 3 cm.
View Solution
