Given : RS and PT are altitudes of ΔPQR. Prove that:
ΔPQT~ΔQRS.
To prove that triangle ΔPQT is similar to triangle ΔQRS, we will use the Angle-Angle (AA) similarity criterion. Here are the steps to prove the similarity:
Step 1: Identify the angles
In triangles ΔPQT and ΔQRS, we need to identify the angles.
Step 2: Establish the right angles
Since RS and PT are altitudes, we know that:
- ∠PTQ=90∘ (because PT is an altitude)
- ∠RSQ=90∘ (because RS is an altitude)
Step 3: State the common angle
Next, we observe that both triangles share a common angle:
- ∠Q is common to both triangles ΔPQT and ΔQRS.
Step 4: List the angles
Now we can list the angles we have:
1. ∠PTQ=90∘
2. ∠RSQ=90∘
3. ∠PQT=∠RQS (common angle)
Step 5: Apply the AA similarity criterion
Since we have two angles in ΔPQT that are equal to two angles in ΔQRS:
- ∠PTQ=∠RSQ
- ∠PQT=∠RQS
By the AA similarity criterion, we can conclude that:
ΔPQT∼ΔQRS
Conclusion
Thus, we have proved that triangle ΔPQT is similar to triangle ΔQRS.
---
In triangles ΔPQT and ΔQRS, we need to identify the angles.
Since RS and PT are altitudes, we know that:
- ∠PTQ=90∘ (because PT is an altitude)
- ∠RSQ=90∘ (because RS is an altitude)
Next, we observe that both triangles share a common angle:
- ∠Q is common to both triangles ΔPQT and ΔQRS.
Now we can list the angles we have:
1. ∠PTQ=90∘
2. ∠RSQ=90∘
3. ∠PQT=∠RQS (common angle)
Since we have two angles in ΔPQT that are equal to two angles in ΔQRS:
- ∠PTQ=∠RSQ
- ∠PQT=∠RQS
ΔPQT∼ΔQRS
Thus, we have proved that triangle ΔPQT is similar to triangle ΔQRS.
Topper's Solved these Questions
- SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)BOOK - ICSECHAPTER - SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)EXERCISE - EXERCISE 15(B)
17 Videos
- SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)BOOK - ICSECHAPTER - SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)EXERCISE - EXERCISE 15(C)
24 Videos
- SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)BOOK - ICSECHAPTER - SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)EXERCISE - EXERCISE 15(E)
61 Videos
- SIMILARITY BOOK - ICSECHAPTER - SIMILARITY EXERCISE - MULTIPLE CHOICE QUESTIONS (COMPETENCY BASED QUESTIONS)
10 Videos
- SOLVING (SIMPLE) PROBLEMS (BASED ON QUADRATIC EQUATIONS)BOOK - ICSECHAPTER - SOLVING (SIMPLE) PROBLEMS (BASED ON QUADRATIC EQUATIONS)EXERCISE - Exercise 6(e )
18 Videos
Similar Questions
Given : RS and PT are altitudes of ΔPQR. Prove that:
PQ×QS=RQ×QT.
View SolutionIn the following figures, the sides AB and BC and the median AD of triangle ABC are respectively equal to the sides PQ and QR and median PS of the triangle PQR. Prove that ΔABCandΔPQR are congruent.

View SolutionThe given figure shows PQ=PRand∠Q=∠R.
Prove that ΔPQS=ΔPRT
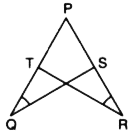
View SolutionS and T are points on sides PR and QR of ΔPQR such that ∠P=∠RTS Show that ΔRPQ~ΔRTS
View SolutionIn a triangle PQR, L and M are two points on the base QR, such that ∠LPQ=∠QRP and ∠RPM=∠RQP. Prove that:
ΔPQL~ΔRPM
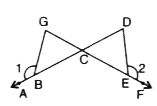
View SolutionIn the given figure , BC = CE and ∠1=∠2.
Prove that :
ΔGCB=ΔDCB .
View SolutionIn the adjoining figure, ABC is a triangle right-angled at vertex A and AD is altitude.
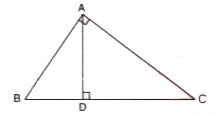
Prove that : ΔABD is similar to ΔCAD.
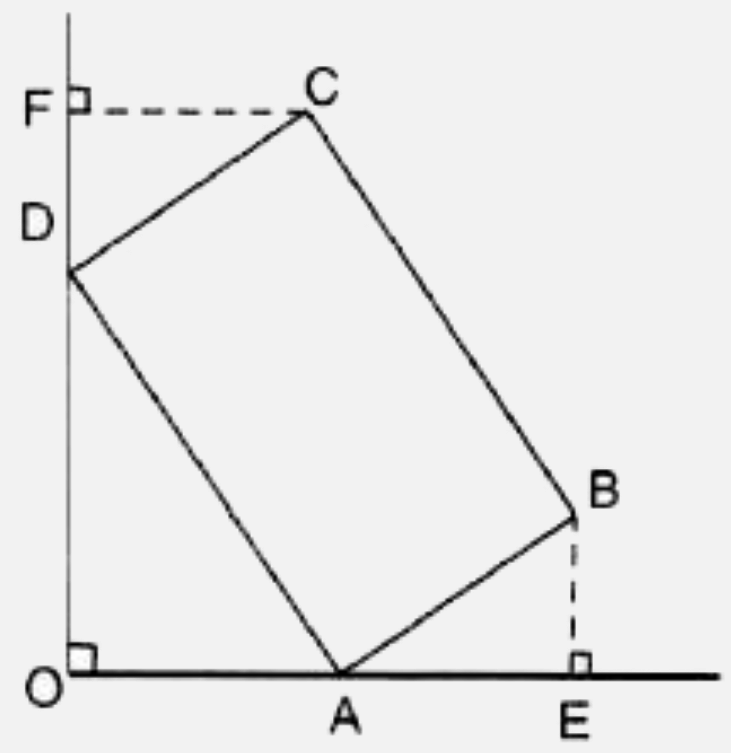
View SolutionIn the given figures , ABCD is a rectangle
Prove that : ΔABE≅ΔCDF.
View SolutionIn ΔPQR.PS⊥QR.PS=11cmand area of ΔPQR=77sq.cmIfareaofDelta PSQ: areaofDelta PSR = 3:4. f∈dQS and SR.
View SolutionTriangle ABC is similar to triangle PQR. If AD and PM are altitudes of the two triangles, prove that : ABPQ=ADPM
View Solution
