In quadrilateral PQRS , PS = QR and ∠SPQ=∠RQP . Prove that :
PR=QS
To prove that PR=QS in quadrilateral PQRS given that PS=QR and ∠SPQ=∠RQP, we can follow these steps:
Step 1: Identify the Given Information
We are given:
- PS=QR (1)
- ∠SPQ=∠RQP (2)
Step 2: Draw the Quadrilateral
Draw quadrilateral PQRS with points P,Q,R,S labeled appropriately. Mark the sides PS and QR as equal, and the angles ∠SPQ and ∠RQP as equal.
Step 3: Form Triangles
Consider triangles △SPQ and △RQP.
Step 4: Apply the Side-Angle-Side (SAS) Congruence Criterion
We can state:
- Side PS=QR (from (1))
- Angle ∠SPQ=∠RQP (from (2))
- Side PQ=PQ (common side)
Thus, by the Side-Angle-Side (SAS) criterion, we can conclude:
△SPQ≅△RQP
Step 5: Use Corresponding Parts of Congruent Triangles (CPCTC)
Since the triangles SPQ and RQP are congruent, we can state that their corresponding parts are equal. Therefore:
SQ=PR
Conclusion
Thus, we have proved that PR=QS.
---
We are given:
- PS=QR (1)
- ∠SPQ=∠RQP (2)
Draw quadrilateral PQRS with points P,Q,R,S labeled appropriately. Mark the sides PS and QR as equal, and the angles ∠SPQ and ∠RQP as equal.
Consider triangles △SPQ and △RQP.
We can state:
- Side PS=QR (from (1))
- Angle ∠SPQ=∠RQP (from (2))
- Side PQ=PQ (common side)
△SPQ≅△RQP
Since the triangles SPQ and RQP are congruent, we can state that their corresponding parts are equal. Therefore:
SQ=PR
Thus, we have proved that PR=QS.
Topper's Solved these Questions
- CHAPTERWISE REVISION (STAGE 3) BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 3) EXERCISE - ISOSCELES TRIANGLES
2 Videos
- CHAPTERWISE REVISION (STAGE 3) BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 3) EXERCISE - INEQUALITIES
7 Videos
- CHAPTERWISE REVISION (STAGE 3) BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 3) EXERCISE - LOGARITHM
9 Videos
- CHAPTERWISE REVISION (STAGE 1) BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 1) EXERCISE - Graphical solution
10 Videos
- CIRCLEBOOK - ICSECHAPTER - CIRCLEEXERCISE - EXERCISE 17(D)
12 Videos
Similar Questions
In quadrilateral PQRS , PS = QR and ∠SPQ=∠RQP . Prove that :
∠QPR=∠PQS
View SolutionIn a quadrilateral ABCD, AB = CD and ∠B=∠C. Prove that
AC=AB
View SolutionIn a quadrilateral ABCD, AB = CD and ∠B=∠C. Prove that
AD is parallel to BC.
View SolutionThe given figure shows PQ=PRand∠Q=∠R.
Prove that ΔPQS=ΔPRT
View SolutionIn the given figure, ∠SPR=∠QRP and ∠RSP=∠PQR. Prove that :
(i) PQ=RS
(ii) PS=QR

View SolutionIn quadrilateral ABCD, AD = BC and BD = CA. Prove that :
(i) ∠ADB=∠BCA
(ii) ∠DAB=∠CBA
View SolutionIn a triangle PQR, L and M are two points on the base QR, such that ∠LPQ=∠QRP and ∠RPM=∠RQP. Prove that:

QL×RM=PL×PM
View SolutionIn ΔPQR, If ∠R>∠Q, then
View SolutionIn a triangle PQR, L and M are two points on the base QR, such that ∠LPQ=∠QRP and ∠RPM=∠RQP. Prove that:
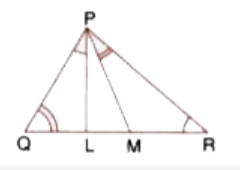
PQ2=QR×QL
View SolutionIn the adjoining figure PQ = PR and ∠PRQ=70∘ Find ∠QPR.
View Solution
