In the given figure PT touches a circle with centre O at R. Diameter SQ when produced meets PT at P. If ∠SPR=x∘ and ∠QRP=y∘, show what x∘+2y∘=90∘
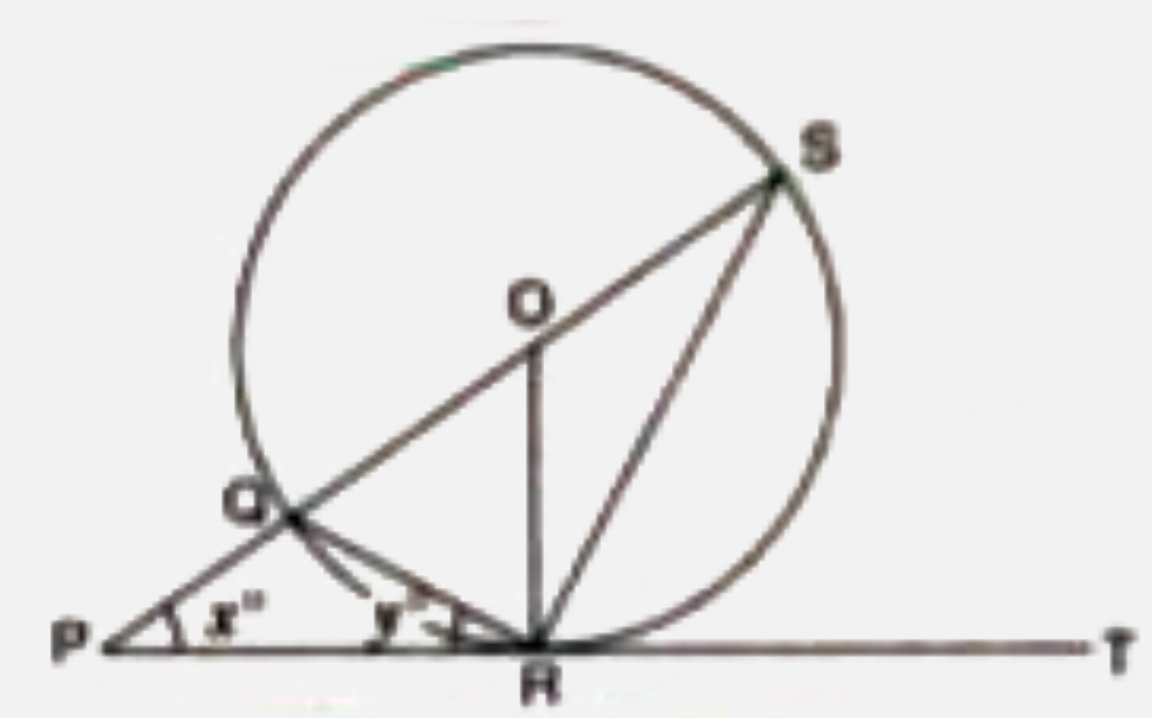
The correct Answer is:90∘
Step by step video & image solution for In the given figure PT touches a circle with centre O at R. Diameter SQ when produced meets PT at P. If /_SPR=x^(@) and /_QRP=y^(@), show what x^(@)+2y^(@)=90^(@) by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TANGENTS AND INTERSECTING CHORDSBOOK - ICSECHAPTER - TANGENTS AND INTERSECTING CHORDSEXERCISE - EXERCISE 18(A)
24 Videos
- TANGENTS AND INTERSECTING CHORDSBOOK - ICSECHAPTER - TANGENTS AND INTERSECTING CHORDSEXERCISE - EXERCISE 18 (B)
18 Videos
- SPECIMEN QUESTION PAPER (MATHEMATICS)BOOK - ICSECHAPTER - SPECIMEN QUESTION PAPER (MATHEMATICS)EXERCISE - Section C
12 Videos
- TRIGONOMETRICAL IDENTITIESBOOK - ICSECHAPTER - TRIGONOMETRICAL IDENTITIESEXERCISE - QUESTIONS
22 Videos
Similar Questions
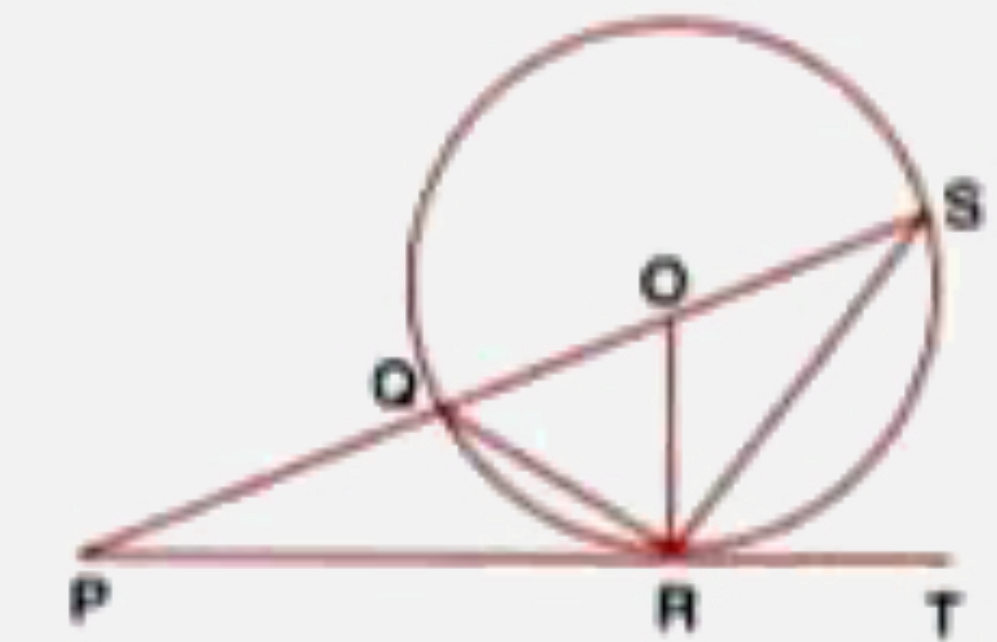
In the given figure, PT touches the circle with centre O at point R. Diameter SQ is produced to meet the tangent TR at P.
Given ∠SPR=x∘ and ∠QRP=y∘,
prove that
(i) ∠ORS=y∘
ii. Write an expression connecting x and y.
View SolutionThe given figure shows a circle with centre O and BCD is tangent to it at C. Show that
∠ACD+∠BAC=90∘

View SolutionIn the given figure, PT is a tangent to the circle with centre O. If OT=6cm and OP=10cm, thcn find the length of tangent PT.
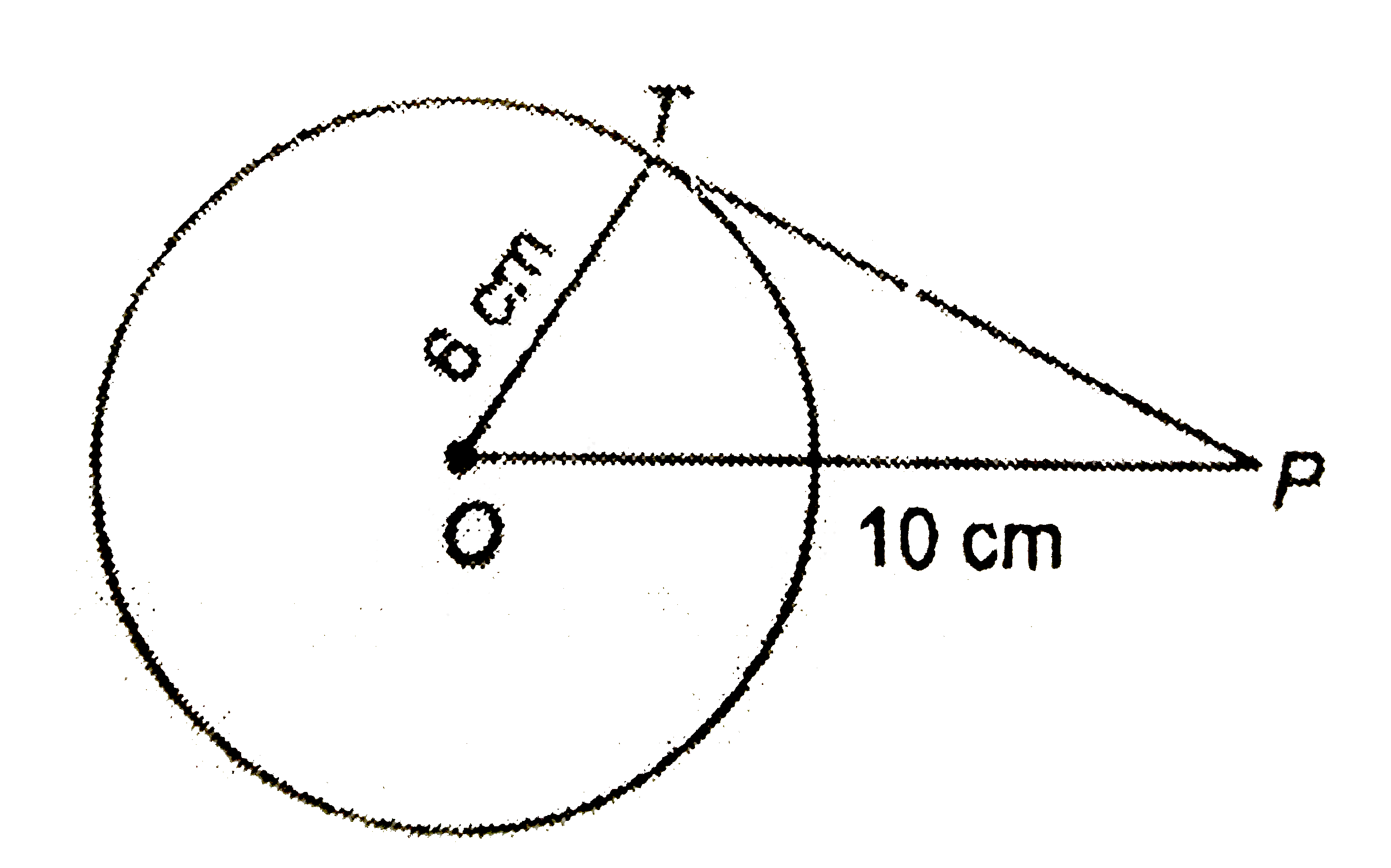
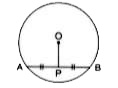
View SolutionThe given figure shows a circle with centre O. P is mid-point of chord AB.
Show that OP is perpendicular to AB.
View SolutionThe equal chords AB and CD of circle with centre O, when produced, meet at P outside the circle. Prove that :
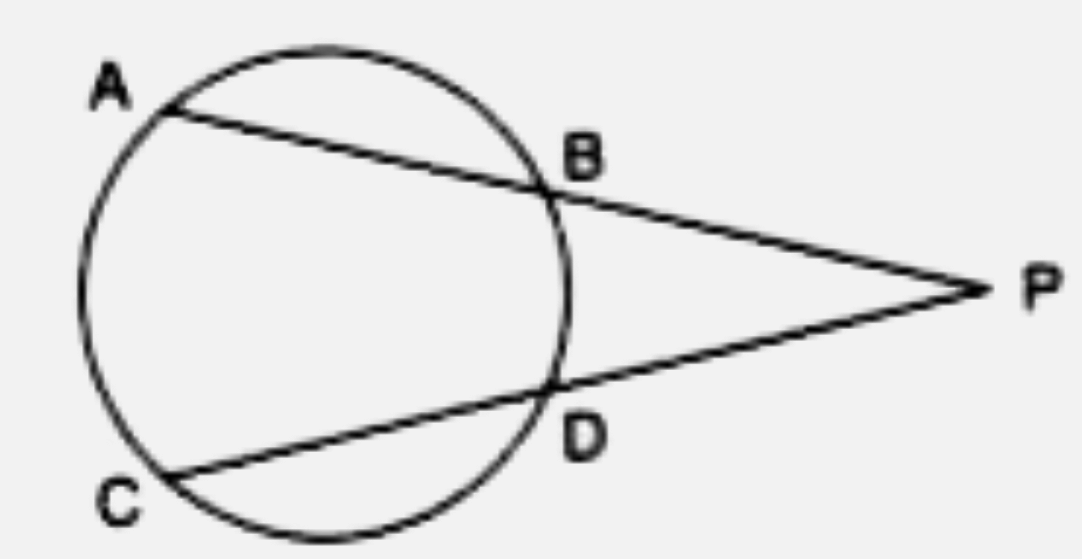
PA=PC.
View SolutionThe equal chords AB and CD of circle with centre O, when produced, meet at P outside the circle. Prove that :

PB=PD
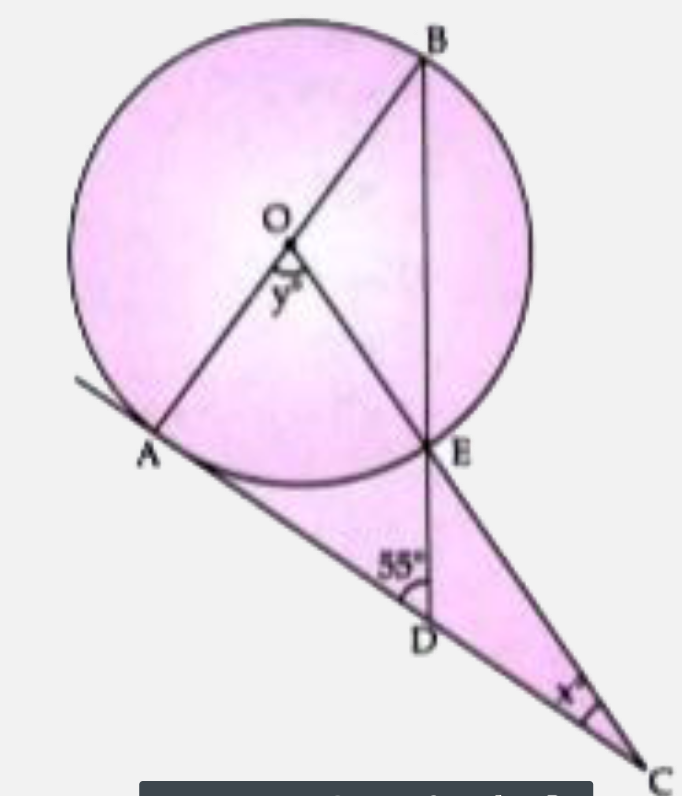
View SolutionIn the given figure AC is a tangent to the circle with centre O.
If ∠ADB=55∘, find x and y. Give reason for your answer.
View Solution. In the given figure, two equal circles, with centres O and O', touch each other at X. OO' produced me the circle with centre O' at A. AC is tangent to the circle with centreO, at the point C. O'D is perpendicular to AC. Find the value of DO'CO.
View Solution. In the given figure, two equal circles, with centres O and O', touch each other at X. OO' produced me the circle with centre O' at A. AC is tangent to the circle with centreO, at the point C. O'D is perpendicular to AC. Find the value of DO'CO.
View SolutionIn the given figure, ∠ABC=90∘ and BC is diameter of the given circle. Show that:
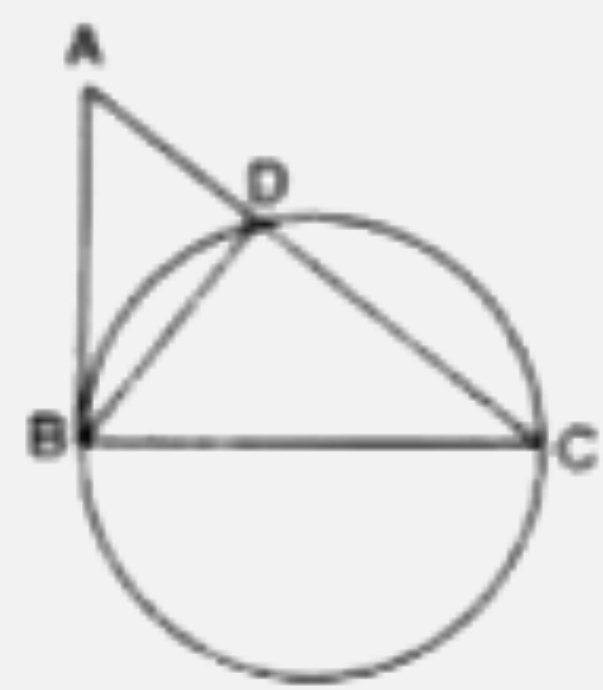
AC×AD=AB2
View Solution
