If ∆ABC ~ ∆PQR, perimeter of ∆ABC = 32 cm, perimeter of ∆PQR = 48 cm and PR = 6 cm, then find the length of AC.
The correct Answer is:4 cm
To solve the problem step by step, we will use the properties of similar triangles and the relationship between their perimeters.
Step 1: Understand the relationship between the triangles
Since triangles ABC and PQR are similar, the ratios of their corresponding sides are equal to the ratios of their perimeters.
Step 2: Write the ratio of the perimeters
The ratio of the perimeters of triangles ABC and PQR can be expressed as:
Perimeter of △ABCPerimeter of △PQR=32 cm48 cm
Step 3: Simplify the ratio
We can simplify the ratio:
3248=23
Step 4: Set up the proportion for the sides
Let AC be the side corresponding to PR in triangle PQR. Since PR = 6 cm, we can set up the proportion:
ACPR=23
Substituting PR into the equation gives:
AC6=23
Step 5: Solve for AC
To find AC, we can cross-multiply:
3⋅AC=2⋅6
This simplifies to:
3⋅AC=12
Now, divide both sides by 3:
AC=123=4 cm
Conclusion
The length of AC is 4 cm.
Since triangles ABC and PQR are similar, the ratios of their corresponding sides are equal to the ratios of their perimeters.
The ratio of the perimeters of triangles ABC and PQR can be expressed as:
Perimeter of △ABCPerimeter of △PQR=32 cm48 cm
We can simplify the ratio:
3248=23
Let AC be the side corresponding to PR in triangle PQR. Since PR = 6 cm, we can set up the proportion:
ACPR=23
Substituting PR into the equation gives:
AC6=23
To find AC, we can cross-multiply:
3⋅AC=2⋅6
This simplifies to:
3⋅AC=12
Now, divide both sides by 3:
AC=123=4 cm
The length of AC is 4 cm.
Topper's Solved these Questions
- MEASURES OF CENTRAL TENDENCY (MEAN, MEDIAN, QUARTILES AND MODE)BOOK - ICSECHAPTER - MEASURES OF CENTRAL TENDENCY (MEAN, MEDIAN, QUARTILES AND MODE)EXERCISE - EXERCISE 24 (A)
17 Videos
- MEASURES OF CENTRAL TENDENCY (MEAN, MEDIAN, QUARTILES AND MODE)BOOK - ICSECHAPTER - MEASURES OF CENTRAL TENDENCY (MEAN, MEDIAN, QUARTILES AND MODE)EXERCISE - EXERCISE 24 (B)
10 Videos
- MATRICESBOOK - ICSECHAPTER - MATRICESEXERCISE - Exercise 9D
25 Videos
- MIXED PRACTICE BOOK - ICSECHAPTER - MIXED PRACTICE EXERCISE - SET B
52 Videos
Similar Questions
Knowledge Check
The perimeter of an isosceles triangle is 59 cm. If the base is 23cm, find the length of the equal sides.
A16cmB18cmC17cmD14cm
In ΔPQR, If angleR=angleP, QR=4 cm and PR = 5 cm. Then, the length of PQ is
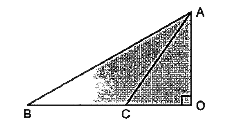
View SolutionIn triangle ABC, given below, AB = 8 cm, BC = 6 cm and AC = 3 cm. Calculate the length of OC
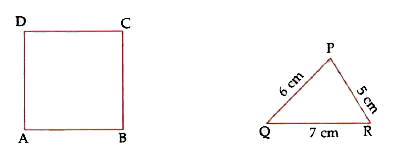
View SolutionThe perimeter of a square ABCD is twice the perimeter of ΔPQR. Find the area of the square ABCD
View SolutionIf ΔABC~ΔDEF, AB=4cm, DE=6, EF=9 cm and FD=12 cm, then find the perimeter of ΔABC.
View Solution∆ABC ~ ∆DEF. If AB = 4 cm, BC = 3.5 cm, CA = 2.5 cm and DF = 7.5 cm, find the perimeter of ∆DEF
View SolutionPQR is a triangle. S is a point on the side QR of ΔPQR such that ∠PSR=∠QPR. Given QP = 8 cm, PR = 6 cm and SR = 3 cm.

Find the lengths of QR and PS.
View SolutionFind the perimeters of :
A rhombus having each side of length 6.3 cm .
View Solution
