If ΔABC~ΔDEF, AB=4cm, DE=6, EF=9 cm and FD=12 cm, then find the perimeter of ΔABC.
To find the perimeter of triangle ABC given that triangle ABC is similar to triangle DEF, we can follow these steps:
1. Identify the given values:
- AB = 4 cm
- DE = 6 cm
- EF = 9 cm
- FD = 12 cm
2. Set up the ratio of corresponding sides:
Since the triangles are similar, the ratios of their corresponding sides are equal. Therefore, we can write:
ABDE=BCEF=ACFD
3. Calculate BC using the ratio of AB and DE:
Using the first part of the ratio:
ABDE=46
We can set up the equation:
46=BC9
Cross-multiplying gives:
4×9=6×BC
36=6×BC
Dividing both sides by 6:
BC=366=6 cm
4. Calculate AC using the ratio of BC and EF:
Now using the second part of the ratio:
BCEF=69
Set up the equation:
69=AC12
Cross-multiplying gives:
6×12=9×AC
72=9×AC
Dividing both sides by 9:
AC=729=8 cm
5. Calculate the perimeter of triangle ABC:
The perimeter of triangle ABC is the sum of its sides:
Perimeter=AB+BC+AC=4+6+8
Perimeter=18 cm
Final Answer:
The perimeter of triangle ABC is 18 cm.
- AB = 4 cm
- DE = 6 cm
- EF = 9 cm
- FD = 12 cm
Since the triangles are similar, the ratios of their corresponding sides are equal. Therefore, we can write:
ABDE=BCEF=ACFD
Using the first part of the ratio:
ABDE=46
We can set up the equation:
46=BC9
Cross-multiplying gives:
4×9=6×BC
36=6×BC
Dividing both sides by 6:
BC=366=6 cm
Now using the second part of the ratio:
BCEF=69
Set up the equation:
69=AC12
Cross-multiplying gives:
6×12=9×AC
72=9×AC
Dividing both sides by 9:
AC=729=8 cm
The perimeter of triangle ABC is the sum of its sides:
Perimeter=AB+BC+AC=4+6+8
Perimeter=18 cm
The perimeter of triangle ABC is 18 cm.
Topper's Solved these Questions
- TRIANGLESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - TRIANGLESEXERCISE - Long Answer Type Questions
18 Videos
- TRIANGLESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - TRIANGLESEXERCISE - Very Short Answer Typw Questions
12 Videos
- SURFACE AREAS AND VOLUMESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - LONG ANSWER TYPE QUESTIONS
20 Videos
Similar Questions
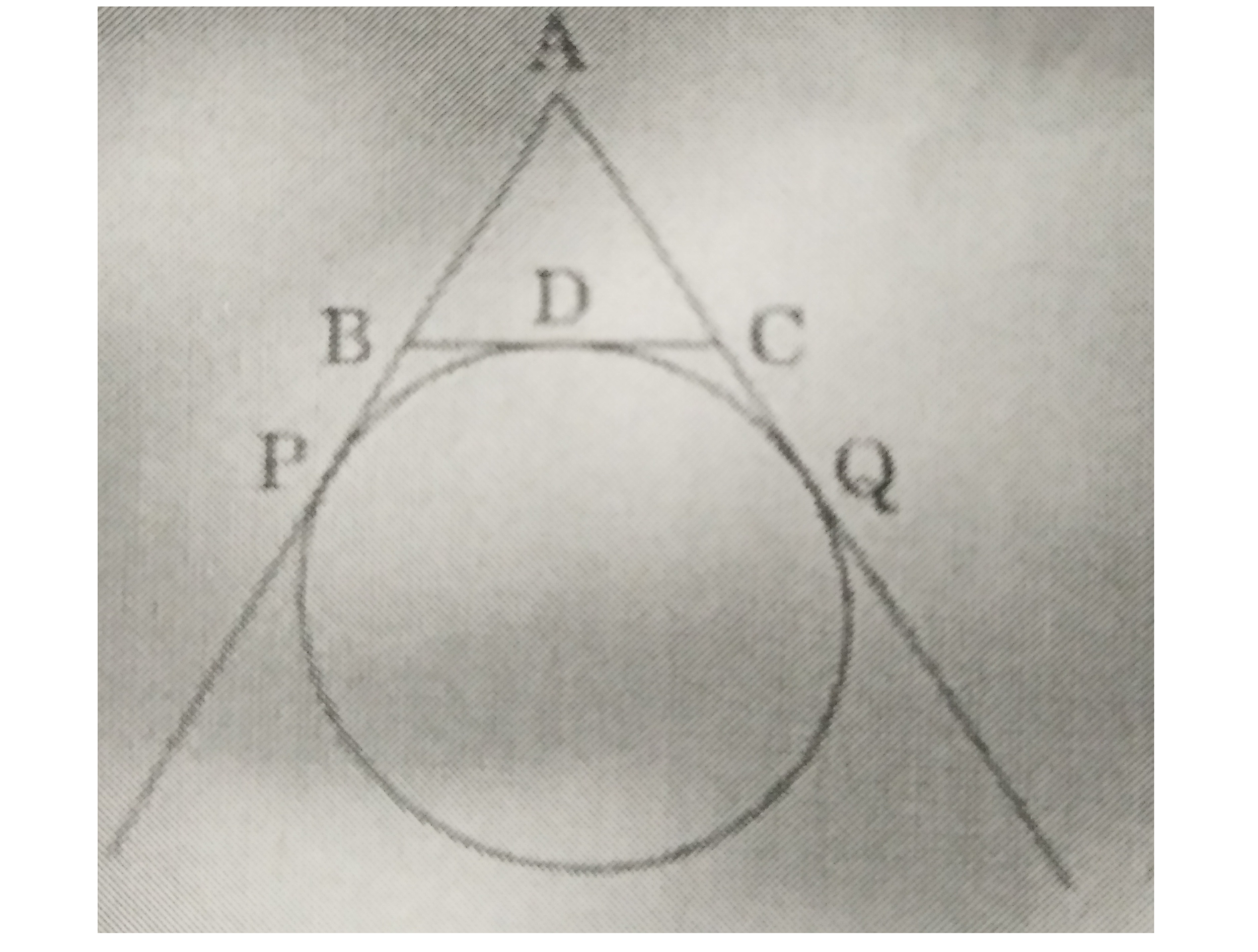
Find the perimeter of ΔABC, if AP=12 cm

View SolutionIn Figure , find the perimeter of ΔABC. If AP = 12 cm.
View SolutionIn ∆DEW, AB || EW. If AD = 4 cm, DE = 12 cm and DW = 24 cm, then find the value of DB.
View Solution∆ABC ~ ∆DEF. If AB = 4 cm, BC = 3.5 cm, CA = 2.5 cm and DF = 7.5 cm, find the perimeter of ∆DEF
View SolutionIt is given that ΔABC~ΔEDF such that AB=5 cm, AC=7 cm, DF= 15 cm and DE = 12 cm. Find the lengths of the remaining sides of the triangles.
View SolutionIn a ΔABC,D,EandF are respectively the mid-points of BC, CA and AB. If the lengths of side AB, BC and CA are 7 cm, 8 cm and 9 cm respectively, find the permeter of ΔDEF.
View SolutionIn ΔABC,∠ABC=∠DAC, AB = 8 cm, AC = 4 cm and AD = 5 cm.
(iii) Find area of ΔACD : area of ΔABC.
View SolutionIn the given figure, AB and DE are perpendicular to BC. If AB = 6cm, DE = 4cm and AC = 15cm.

(iii) Find the ratio of the area of ΔABC : area of ΔDEC.
View SolutionIn the given figure, ΔABC is similar to ΔDEF,AB=(x−0.5) cm, AC=1.5xcm,DE=9cm,andDF=3xcm. Find the lengths of AB and DF.
View SolutionIn ΔABC,∠ABC=∠DAC, AB = 8 cm, AC = 4 cm and AD = 5 cm.
(ii) Find the length of BC and CD.
View Solution
