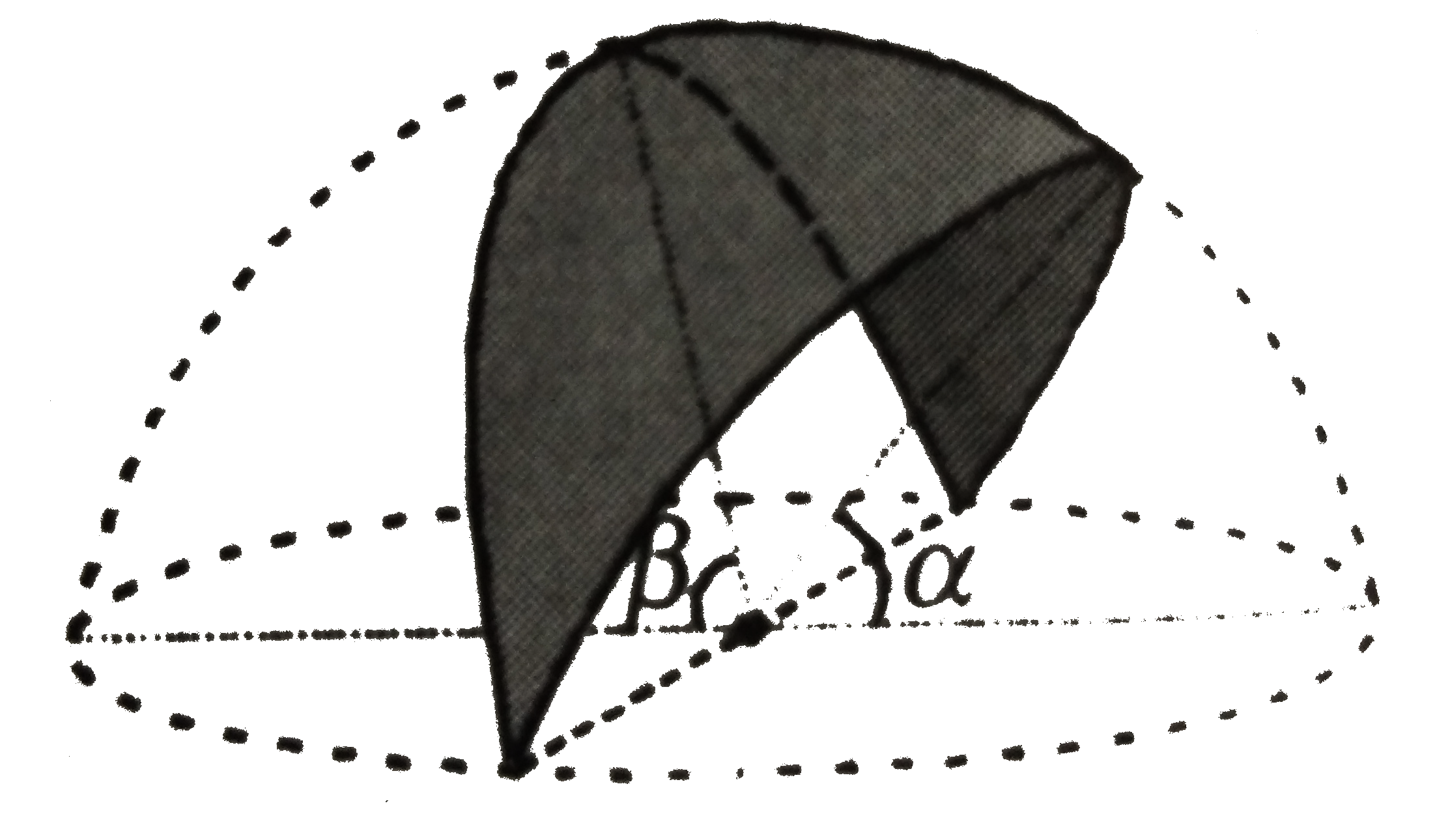
The electric field intensity at the center of a uniformly charged hemispherical shell is $E_{0}$ . Now two portions of the hemisphere are cut from either side, and the remaining portion is shown in fig. If $α = β = π / 3$ , then the electric field intensity at the center due to the remaining portion is

$\frac{E_{0}}{3}$

$\frac{E_{0}}{6}$

$\frac{E_{0}}{2}$

$E_{0}$

Video Solution

Text Solution

Verified by Experts

consider the whole hemispere as three portion if electric field due to one portion is $E_{1}$ then $2 E_{1} sin 30 + E_{1} = E_{0}$
$2 E_{1} = E_{0}$
$\Rightarrow E_{1} = \frac{E_{0}}{2}$

Updated on:21/07/2023

Electric field intensity (E) due to an electric dipole varies with distance (r ) from the point of the center of dipole as :
A $\frac{1}{r} and \frac{1}{r^{2}}$
B $\frac{1}{r^{2}} and \frac{1}{r}$
C $\frac{1}{r^{3}} and \frac{1}{r^{3}}$
D $\frac{1}{r^{3}} and \frac{1}{r^{2}}$