An insect of mass m is initially at one end of a stick of length L and mass M, which rests on a smooth floor. The coefficientg of friction between the insect and the stick is k. The minimum time in which the insect can reach the other end of the stick is t. Then t2 is equal to
2L/kg
2Lm/kg(M+m)
2LM/kg(M+m)
2Lm/kgM
The correct Answer is:C
An insect …………..
Maximum froce of friction =kmg
∴ maximum acceleration of insect =a1=kmgm=kg
and maximum acceleration of stick =a2=kmgM
∴ acceleration of insect with respect to stick
=a=a1−(−a2)=kg(1+mM)
∴L=12at2ort2=2La=2MLkg(M+m)
Topper's Solved these Questions
Similar Questions
A man of mass m walks from end A to the other end B of a boat of mass M and length l. The coefficient of friction between the man and the boat is μ an neglect any resistive force between the boat and the water.
View SolutionWhen a stick of length L mass M intially upright on a fricitionless floor starts falling the
View SolutionA man of mass m stands at the left end of a uniform plank of length L and mass M, which lies on a frictionaless surface of ice. If the man walks to the other end of the plank, then by what distance does the plank slide on the ice?
View SolutionA man of mass m stands at the left end of a uniform plank of length L and mass M, which lies on a frictionaless surface of ice. If the man walks to the other end of the plank, then by what distance does the plank slide on the ice?
View SolutionA man of mass m stands at the left end of a uniform plank of length L and mass M, which lies on a frictionaless surface of ice. If the man walks to the other end of the plank, then by what distance does the plank slide on the ice?
View SolutionA uniform stick of length l and mass m lies on a smooth table. It rotates with angular velocity ω about an axis perpendicular to the table and through one end of the stick. The angular momentum of the stick about the end is
View SolutionA man of mass M stands at one end of a plank of length L Which lies at rest on a frictionless surface . The man walks to the other end of the plank. If the mass of the plank is 3M, the distance that the man moves relative to the ground is
View SolutionA man of mass M stands at one end of a stationary plank of length L, lying on a smooth surface. The man walks to the other end of the plank. If the mass of the plank is M/3, the distance that the man moves relative to the ground is
View SolutionA man of mass M stands at one end of a stationary plank of length L, lying on a smooth surface. The man walks to the other end of the plank. If the mass of the plank is M/3, the distance that the man moves relative to the ground is
View SolutionA uniform disc of mass M and radius R initially stands vertically on the right end of a horizontal plank of mass M and length L, as shown,
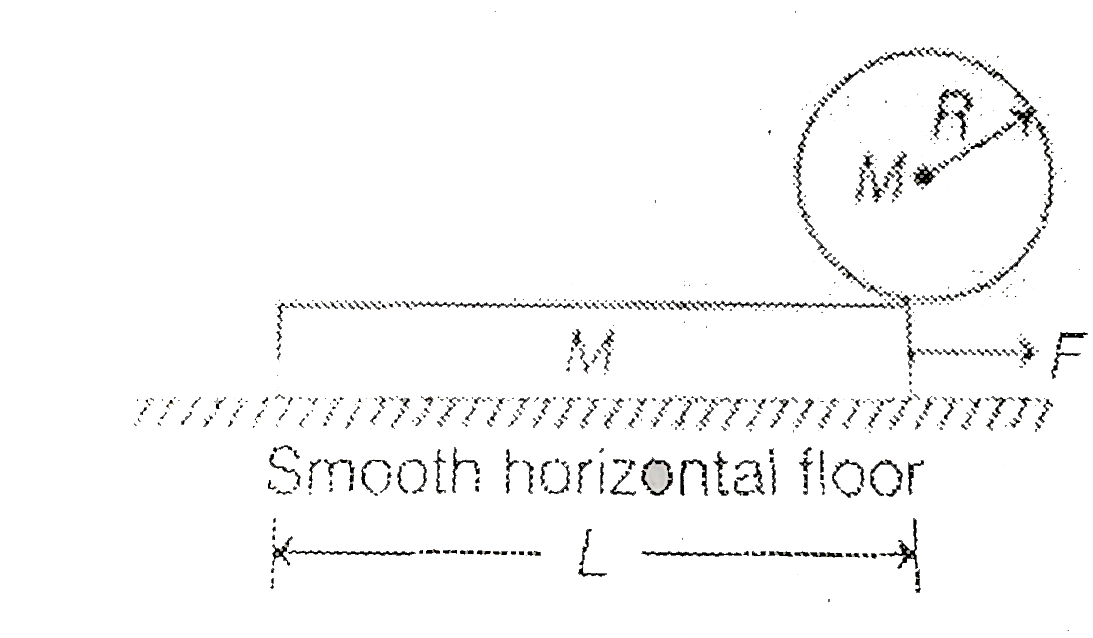
The plank rests on a smooth horizontal floor and friction between disc and plank is sufficiently high such that disc rolls on plank without slipping . The plank is pulled to right with a constant horizontal force of magnitude F.
The distance travelled by centre of disc from its initial position till the left end of plank comes vertically below the centre of disc isView Solution

