Initialy spring is in the natural length and blocks A&B are at rest. Find maximum value of constant force F that can be applied on B such that block A remains at rest. (g=10m/s2) (given answer in Newton)
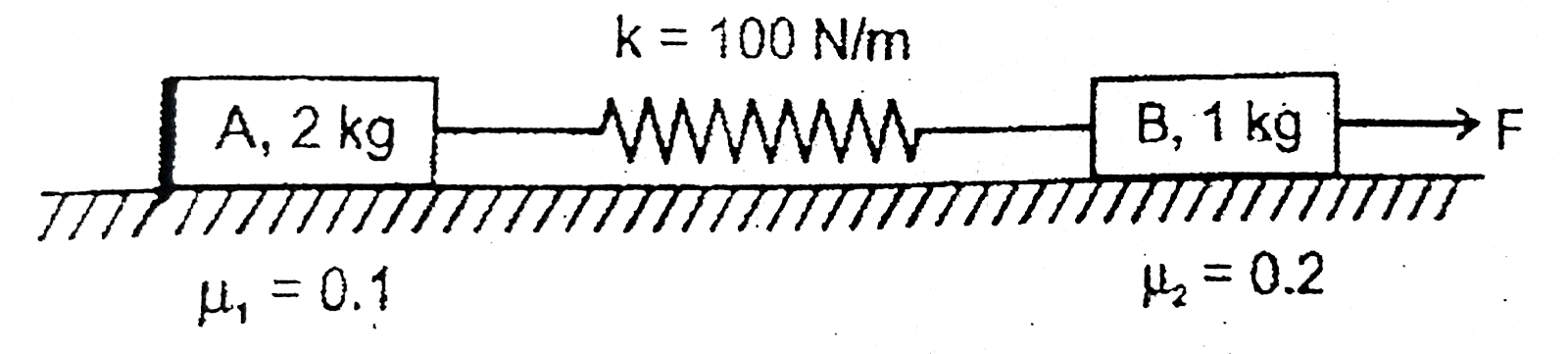
The correct Answer is:3
Initially spring ……………..
Values of μmg for A and B are 2N&2N Worck energy theorm on B gives
Fx−2x−(K/2)x2=0
F=2+kx/2 ……(i)
For equilibrium of Akx=μmg=2
so F=2+1=3N
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
A block A of mass 4 kg is placed on another block B of mass 5 kg and the block rests on a smooth horizontal table. For sliding the block A on B, a horizontal force of 12 N is required to be applied on it. The maximum horizontal force that can be applied on B so that both A and B move together and the acceleration produced by this force is
 A25 N, 5 m/s2B27 N, 3 m/s2C30 N, 8 m/s2Dcannot be calculated from the given data.
A25 N, 5 m/s2B27 N, 3 m/s2C30 N, 8 m/s2Dcannot be calculated from the given data.
The block is always at rest, the maximum force which can be applied for this is 24x. Find the value of x. Take g = 10 m/s2{coefficient of friction = 0.3}
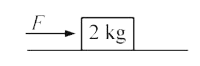 View Solution
View SolutionA block is placed on a smooth inclined plane as shown . For what value of horizontal force F, the block will remain at rest ?
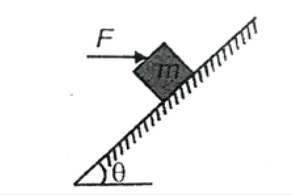 View Solution
View SolutionA spring is attached with a block of mass m and a fixed horizontal roof as shown. The block is lying on a smooth horizontal table and initially the spring is vertical and unstretched. Natural length of spring is 3l0. A constant horizontal force F is applied on the block so that block moves in the direction of force. When length of the spring becomes 5l0, block leaves contact with the table. Find the constant force F, if initial and final velocity of block is zero.
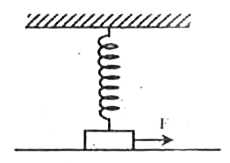 View Solution
View SolutionA block of mass m is attached to a spring of force constant k whose other end is fixed to a horizontal surface. Initially the spring is in its natural length and the block is released from rest. The average force acting on the surface by the spring till the instant when the block has zero acceleration for the first time is
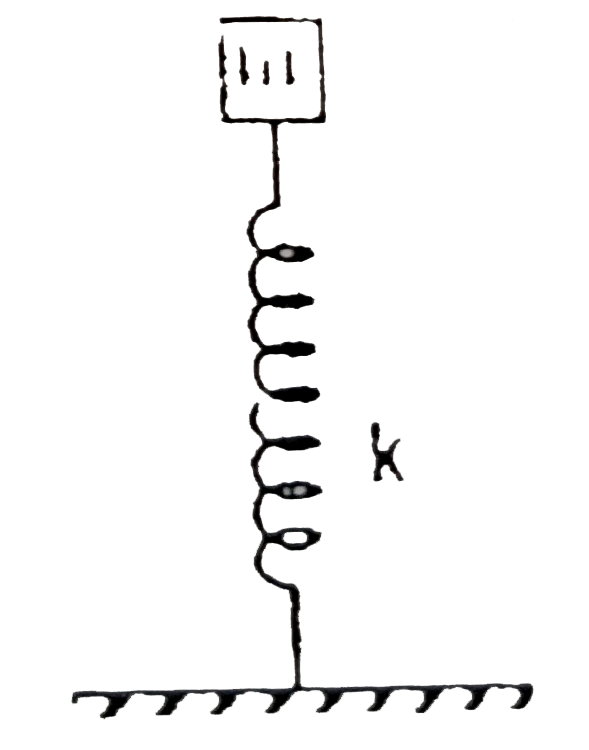 View Solution
View SolutionA block of mass m is placed on another block of mass M lying on a smooth horizontal surface as shown in the figure. The co-efficient of friction between the blocks is μ. Find the maximum horizontal force F (in Newton) that can be applied to the block M so that the blocks together with same acceleration? (M=3kg,m=2kg,μ=0.1,g=10m/s2)
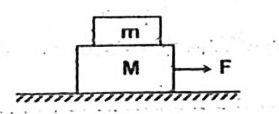 View Solution
View SolutionA block of mass m is connected to a spring (spring constant k). Initially the block is at rest and the spring is in its natural length. Now the system is released in gravitational field and a variable force F is applied on the upper end of the spring such that the downward acceleration of the block is given as a=g−αt, where t is time elapses and α=1m/s2, the velocity of the point of application of the force is:
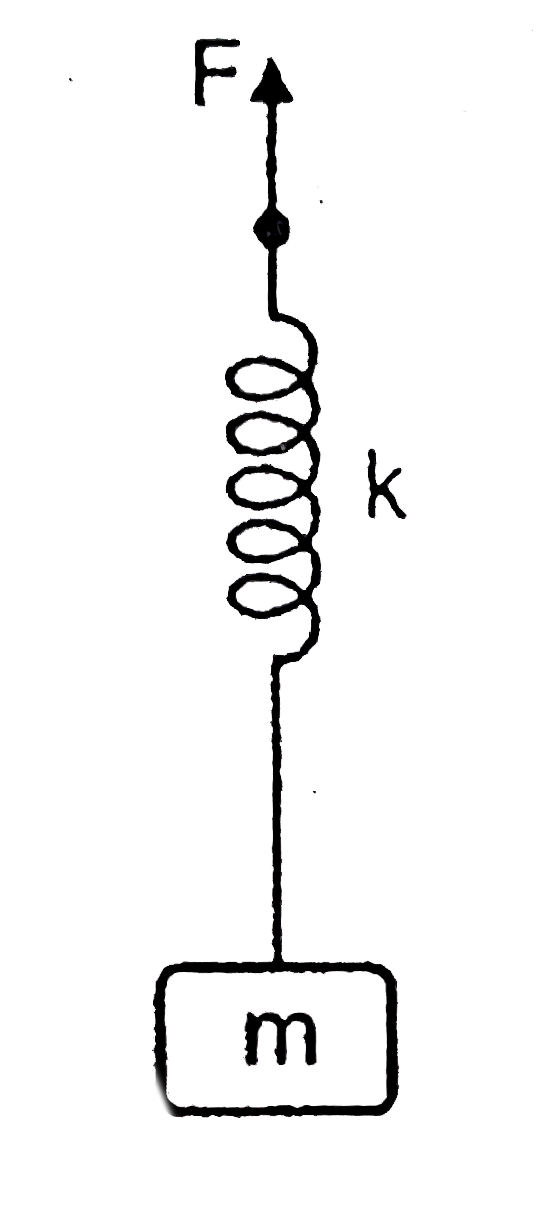 View Solution
View SolutionAs shown in figure, if we apply a horizontal force F on the block, find the maximum force F (in N) that can be applied so that block does not slide up. (Givenθ=45∘,g=10m/sec2,m=15kg,μ=12)
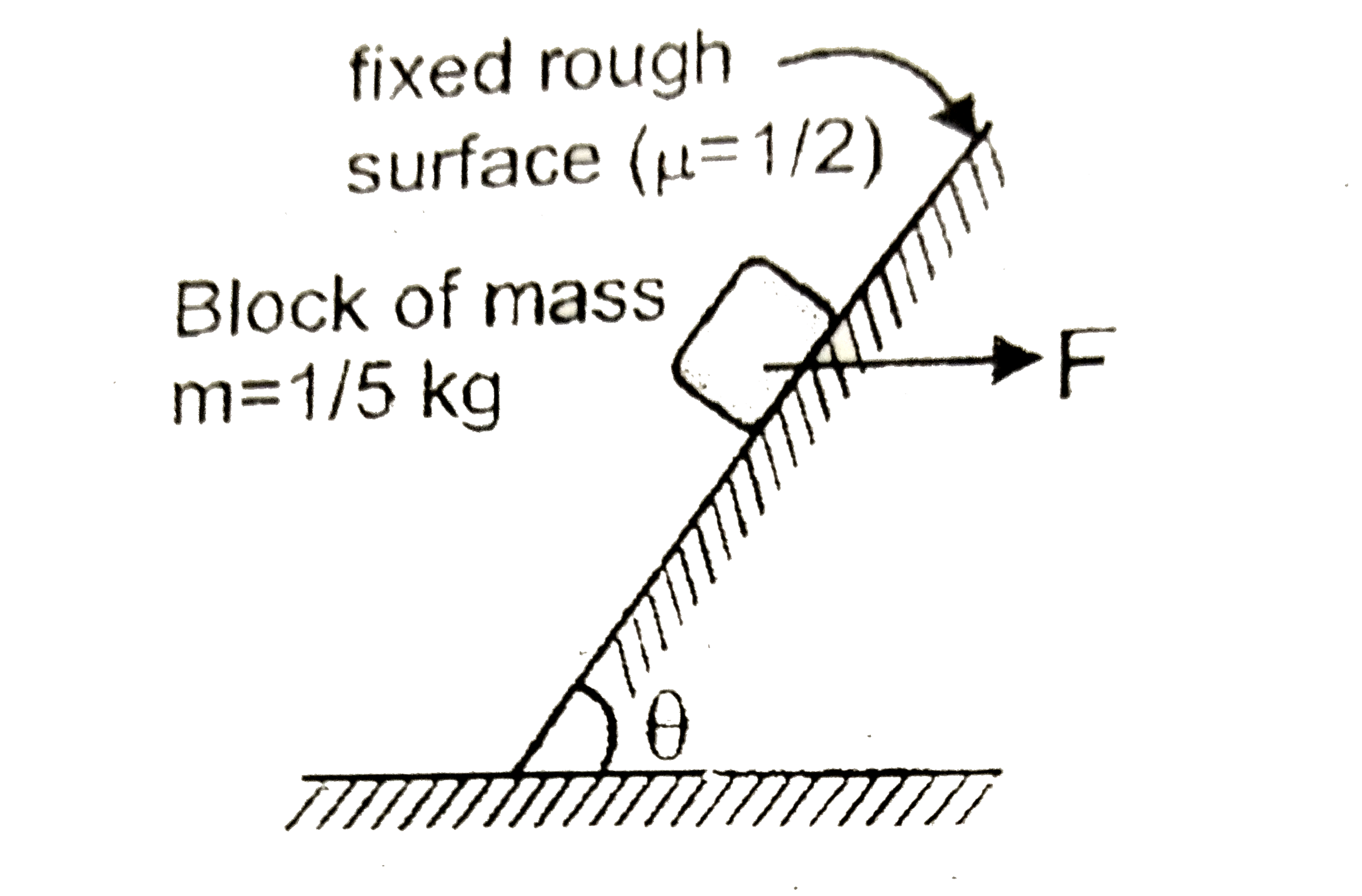 View Solution
View Solution