A rod of mass m=2kg, length l=1m, has uniform cross-section area A=83×10−3m2 but its density is non-uniform. It is hinged about one end kept in water of density ρw=103kg/m3. At the equilibirum, the rod becomes horizontal. Then (g=10m/s2). Choose the correct option(s) :

Centre of mass of the rod is at a distance of 23m from the hinged end
Centre of mass of the rod is at a distance of 34m from the hinged end
Force exerted by the rod on the hinge support is 203N
It we displace the rod slightly by rotating downwards, it will oscillate
The correct Answer is:A, C
A rof of ………….
B=ρlV⊂g=103×(83×10−3)×1×10
B=803N
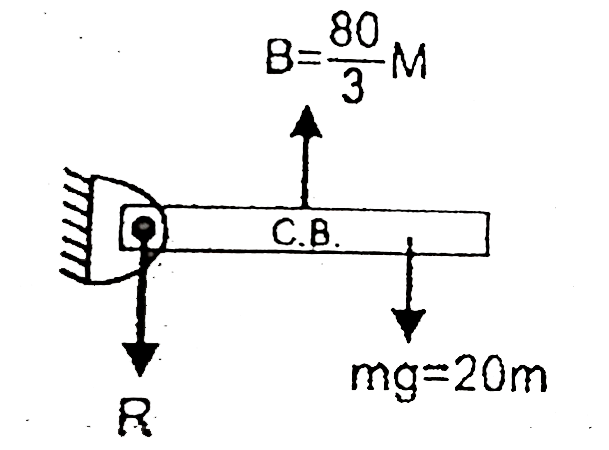
Balancing torque about hinge point,
(803)×12=(20)(x)
(A,B)x=23m
Applying force balance,
R+20=803
(C)R=203M
(D) If we displace the rod, still torque will remain balanced.
Topper's Solved these Questions
Similar Questions
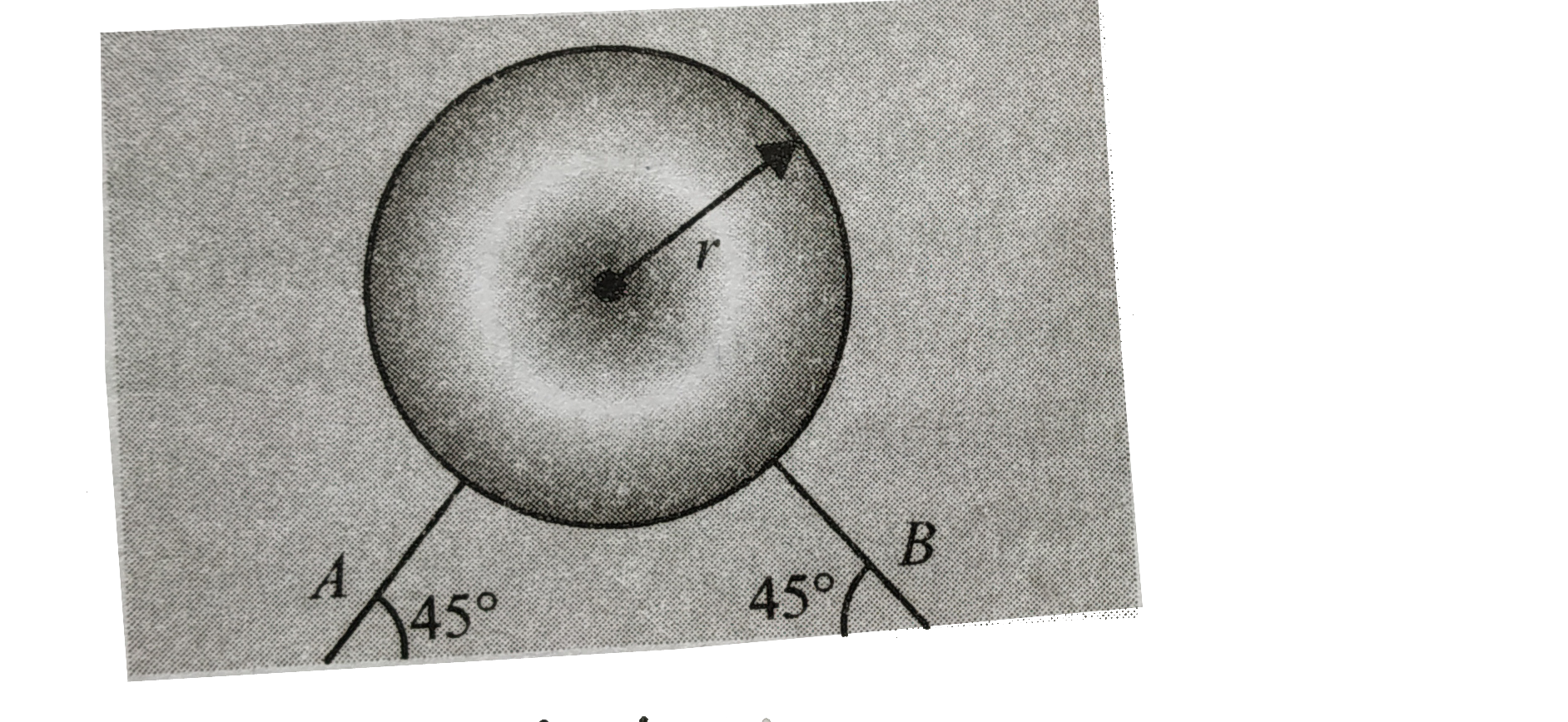
A hollow sphere of mass M=50kg and radius r=(340π)1/3m is immersed in a tank of water (density ρw=103kg/m3). The sphere is tied to the bottom of a tank by two wires A and B as shown. Tension in wire A is (g=10m/s2)
 View Solution
View SolutionThe density of iron is 7.8×103kg m−3 What is its relative density?
View SolutionThe velocity of transverse wave in string whose linear mass density is 3×10−2kgm stretched by a load of 30 kg is (Take g=10ms2)
View SolutionBulk modulus of water is (2.3×109N/m2).Taking average density of waterρ=103kg/m3,find increases in density at a depth of 1km. Take g=10m/s2
View SolutionA tube of small uniform cross section is used to siphon the water from the vessel. Then choose the correct alternative (s) :
(ρwater=103kg/m3,g=10m/s2,Patm=105Pa)
 View Solution
View SolutionRelative density of silver is 10.8. The density of water is 103kgm3. What is the density of silver in SI.
View SolutionA body of mass 10 kg moving at a height of 2 m, with uniform speed of 2 m/s. Its total energy is
View Solution
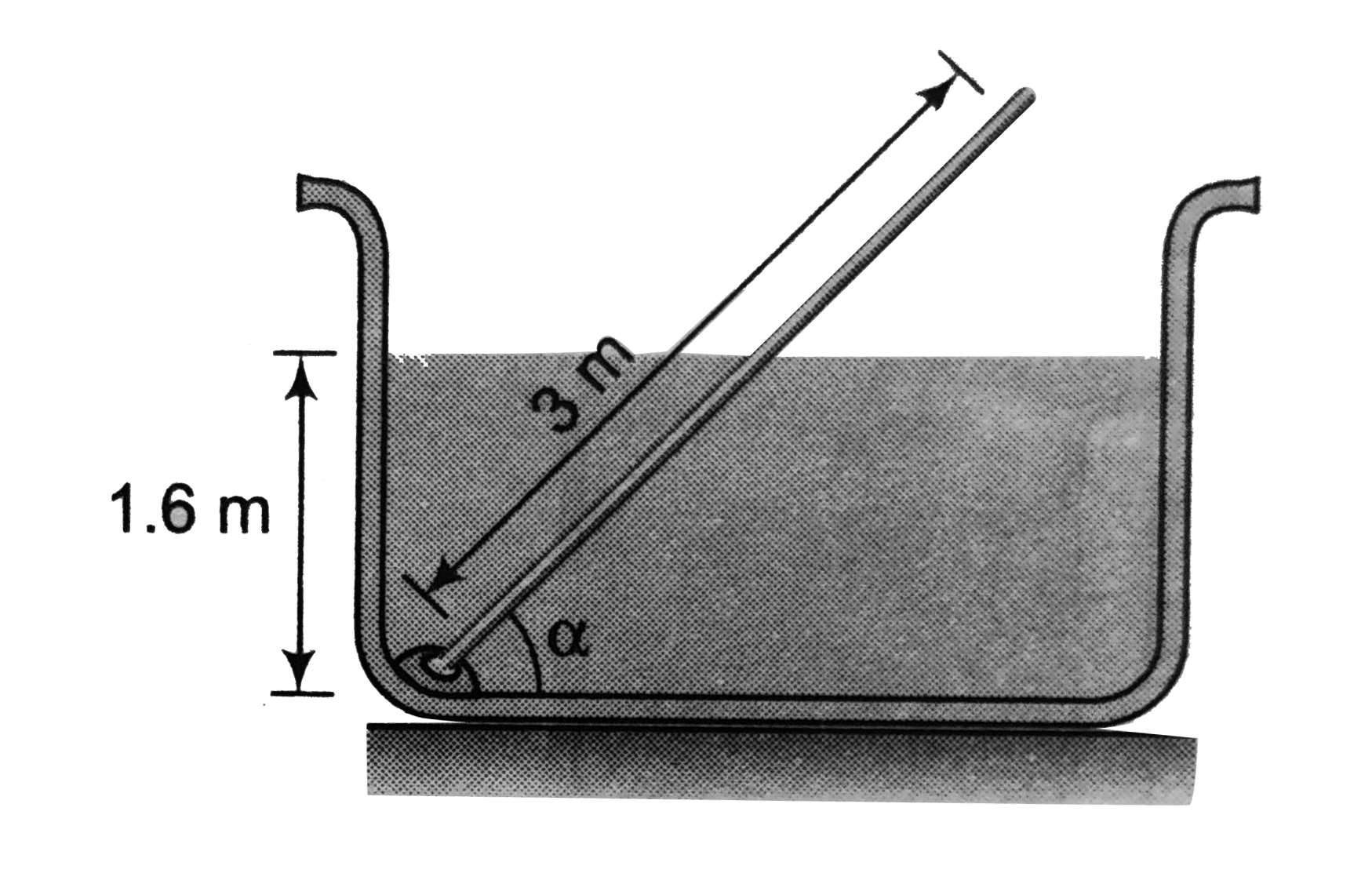
A rod of mass 2 kg ad length 2 m is rotating about its one end O with an angular velocity ω=4rad/s. Find angular momentum of the rod about the axis rotation.View SolutionA wooden rod weighing 25N is mounted on a hinge below the free surface of water as shown. The rod is 3m long and uniform in cross section and the support is 1.6m below the free surface. At what angle α rod is in equilibrium? The cross-section of the rod is 9.5×10−4m2 in area. Density of water is 1000kg/m3. Assume buoyancy to act at centre of immersion. g=9.8m/s2. Also find reaction on the hinge in this position.
 .View Solution
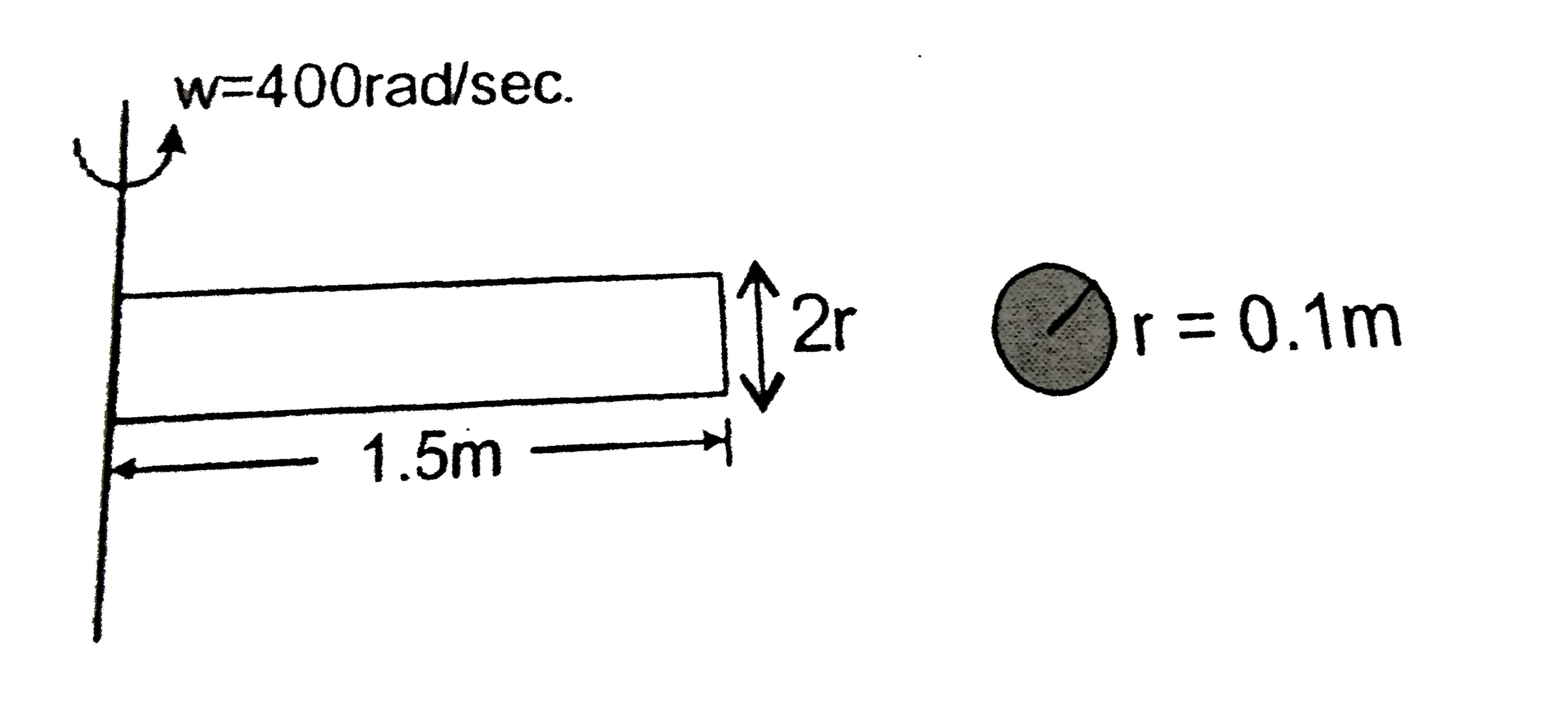
.View SolutionA rod of 1.5m length and uniform density 104kg/m3 is rotating at an angular velocity 400rad/sec about its one end in a horizontal plane. Find out elongation in rod.
Given y=2×1011N/m2
 View Solution
View Solution

