In the figure shown, the minimum force F to be applied perpendicular to the incline so that the block does not slide is

0
40N
120N
200N
The correct Answer is:D
In the …………
For block to be in equilibrium :
F=N+mgcos37∘
f=mgsin37∘
FBD :

For F to be minimum,
For no sliding f≤μN
⇒mgsin37∘≤12[F−mgcos37∘]
⇒2mgsin37∘+mgcos37∘≤F
⇒F≥2mg×35+mg×45⇒F≥2mgi.e.F≥200N
Topper's Solved these Questions
- TEST PAPERSBOOK - RESONANCE ENGLISHCHAPTER - TEST PAPERSEXERCISE - PART - II PHYSICS
106 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Advanced Level Problems
13 Videos
- TEST SERIESBOOK - RESONANCE ENGLISHCHAPTER - TEST SERIESEXERCISE - PHYSICS
130 Videos
Similar Questions
A block of mass m=2kg is resting on a inclined plane of inclination 30∘ as shown in figure The coefficient of friction between the block and the plane is μ=0.5 what minimum force F (in newton) should be applied perpendicular to the plane on the block so that the does not slip on the plane?

View SolutionA block of mass m=2kg is resting on a inclined plane of inclination 30∘ The coefficient of friction between the block and the plane is μ=0.5 what minimum force F (in newton) should be applied perpendicular to the plane on the block so that the does not slip on the plane?

View Solution
Knowledge Check
A block of mass m=2kg is resting on a rough inclined plane of inclination of 30∘ as shown in figure. The coefficient of friction between the block and the plane is μ=0.5. What minimum force F should be applied perpendicular to the plane on the block, so that blocks does not slip on the plane? (g=10m/s2)
 A2.68 NBZeroC4.34 ND6.24 N
A2.68 NBZeroC4.34 ND6.24 N
In the figure shown, horizontal force F1 is applied on a block but the block does not slide. Then as the magnitude of vertical force F2 is increased from zero the block begins to slide, the correct statement is

View SolutionAs shown in figure, if we apply a horizontal force F on the block, find the maximum force F (in N) that can be applied so that block does not slide up. (Givenθ=45∘,g=10m/sec2,m=15kg,μ=12)

View SolutionA cubical block of edge length 1 m and density 800 kg m−3 rests on a rough horizontal surface with coefficient of friction μ. A horizontal force F is applied on the block as shown in figure. If the coefficient of friction is sufficiently large so that the block does not slide bofore toppling, then the minimum value of F to topple the block is [Take g = 10 ms−2]

View SolutionConsider the situation shown in figure. The horizontal surface below the bigger block is smooth. The coefficient of friction between the blocks is μ. Find the minimum and the maximum force F that can be applied in order to keep the smaller block at rest with respect to the bigger block.
View SolutionA bar of mass m is placed on a triangular block of mass M as shown in figure The friction coefficient between the two surface is μ and ground is smooth find the minimum and maximum horizontal force F required to be applied on block so that the bar will not slip on the inclined surface of block

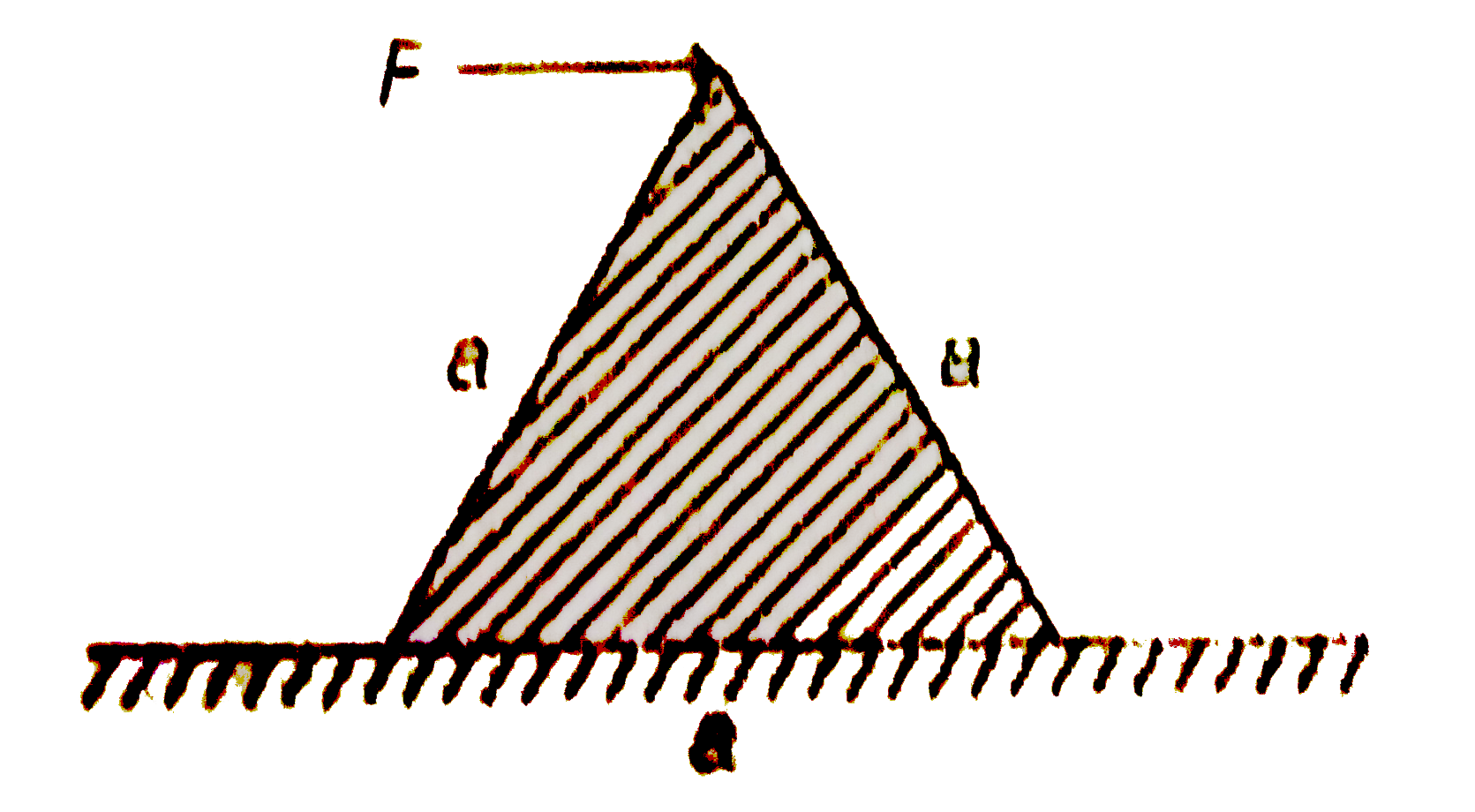
View SolutionAn equilateral prism of mass m rests on a rough horizontal surface with cofficent of friction μ. A horizontal force F is applied on the prism as shown in the figure. If the cofficent of the friction is sufficently high so that the prism does not slide before toppling, then the minimum force required to topple the prism is
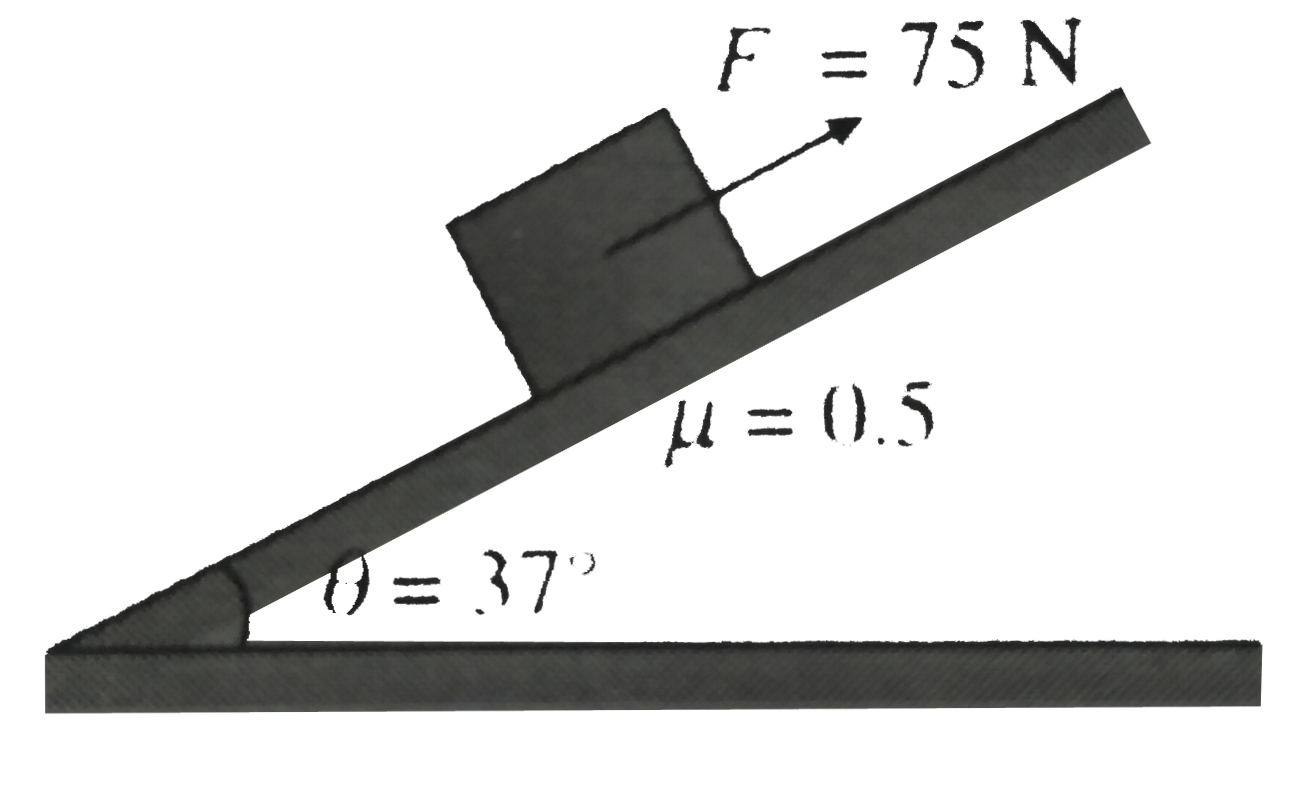
View SolutionA block of mass M=10kg is placed inclined plane , inclined at angle θ=37∘ with horizontal The coefficient of friction between the block and inclined is μ=0.5
a. Calculate the acceleration of the block when it is released
b. Now a force F=75N is appling on block as shown find out the acceleration of the block If the block is initially at rest .
c. In case (b), how much force should be added to 75N force so that block the starts to move up the incline.
d. In case (b), what is the minimum force by which 75N force should be replaced with so that the block does not move?

View Solution
