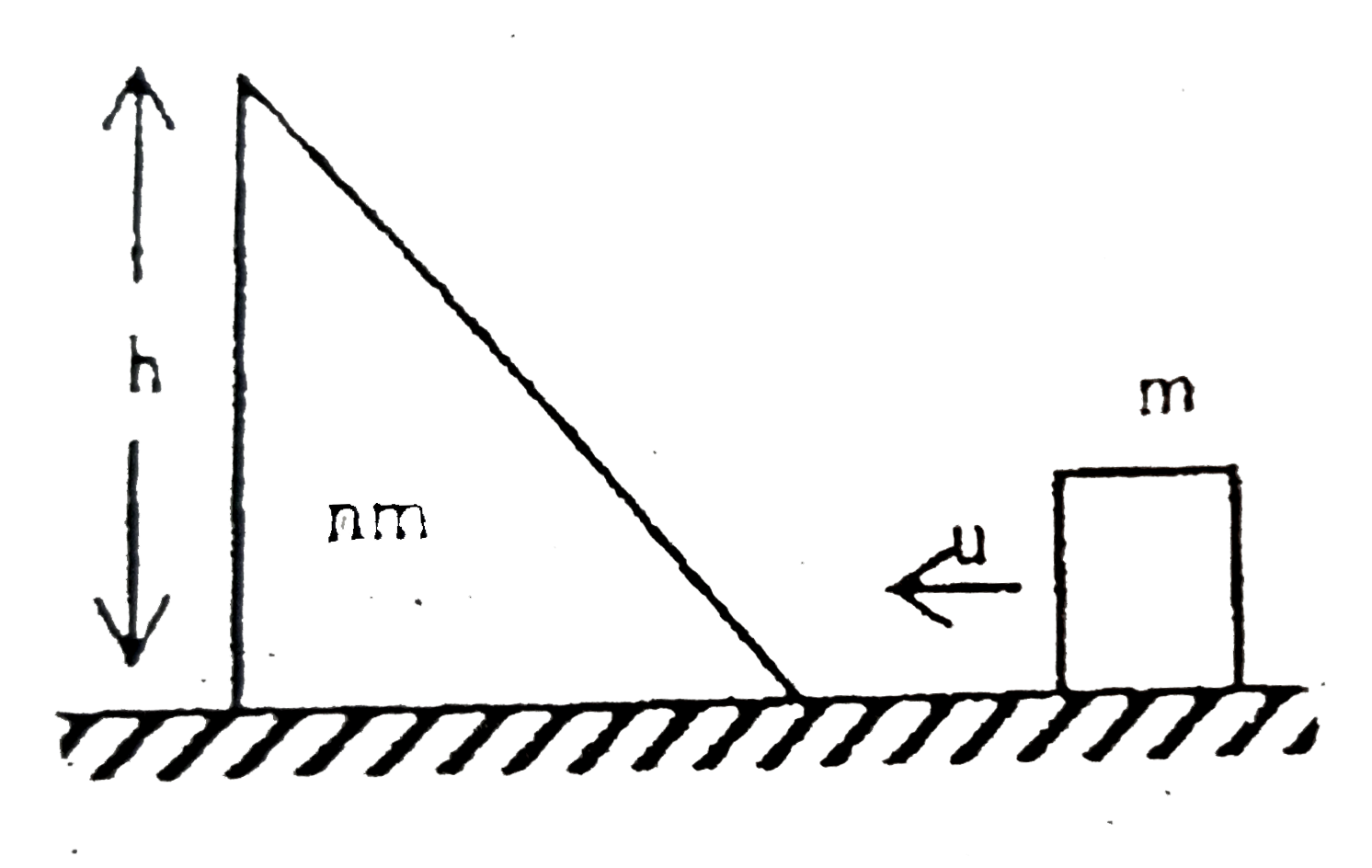
A block of mass m is pushed towards a movable wedge of mass 2 m and height h with a velocity u . All surfaces are smooth . The minimum value of u for which the block will reach the top of the wedge is

√2gh
η√2gh
√2gh(1+1η)
√2gh(1−1η)
The correct Answer is:C
A small block…………..

Applying conservation of momentum.
Let velocity of the system be v, when the mass reaches the tap.
mv=(ηm+m)v , ⇒v=vη+1
Now, applying conservation energy.
12mv∘=12(η+1)m(vη+1)+mgh
⇒12mv2=12m2(η+1)+mgh , ⇒v=√(2gh)(η+1)η
Hence option : (C)
Topper's Solved these Questions
- TEST PAPERSBOOK - RESONANCE ENGLISHCHAPTER - TEST PAPERSEXERCISE - PART - II PHYSICS
106 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Advanced Level Problems
13 Videos
- TEST SERIESBOOK - RESONANCE ENGLISHCHAPTER - TEST SERIESEXERCISE - PHYSICS
130 Videos
Similar Questions
A block of mass m is pushed towards a movable wedge of mass nm and height h, with a velocity u. All surfaces are smooth. The minimum value of u for which the block will reach the top of the wedge is
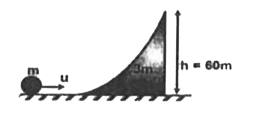
View SolutionA ball of mass 'm' is pushed with a velocity u towards a movable wedge of mass 3m which is at rest. Height of the wedge is 60m. Assume all surfaces to be smooth. The minimum value of 'u' for which the block will reach the top of the wedge is ( There is no loss of energy when the ball tries to rise on the wedge ) ( take g =10m/s2 )
View SolutionThe minimum value of acceleration of wedge for which the block start sliding on the wedge, is:
View SolutionA block of mass 1 kg is moving towards a movable wedge of mass 2 kg as shown in figure. All surfaces are smooth. When the block leaves the wedge from top, its velocity is making an angle θ=30∘ with horizontal.
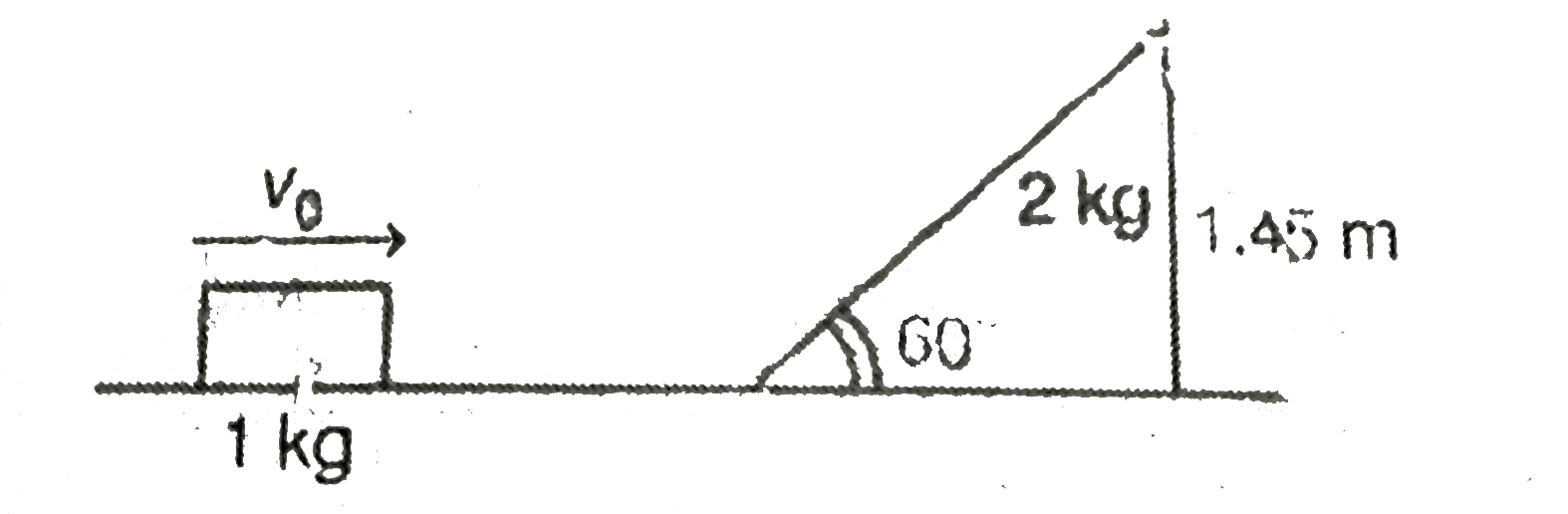
The value of v0 in m/s is
View SolutionA block of mass 1 kg is moving towards a movable wedge of mass 2 kg as shown in figure. All surfaces are smooth. When the block leaves the wedge from top, its velocity is making an angle θ=30∘ with horizontal.
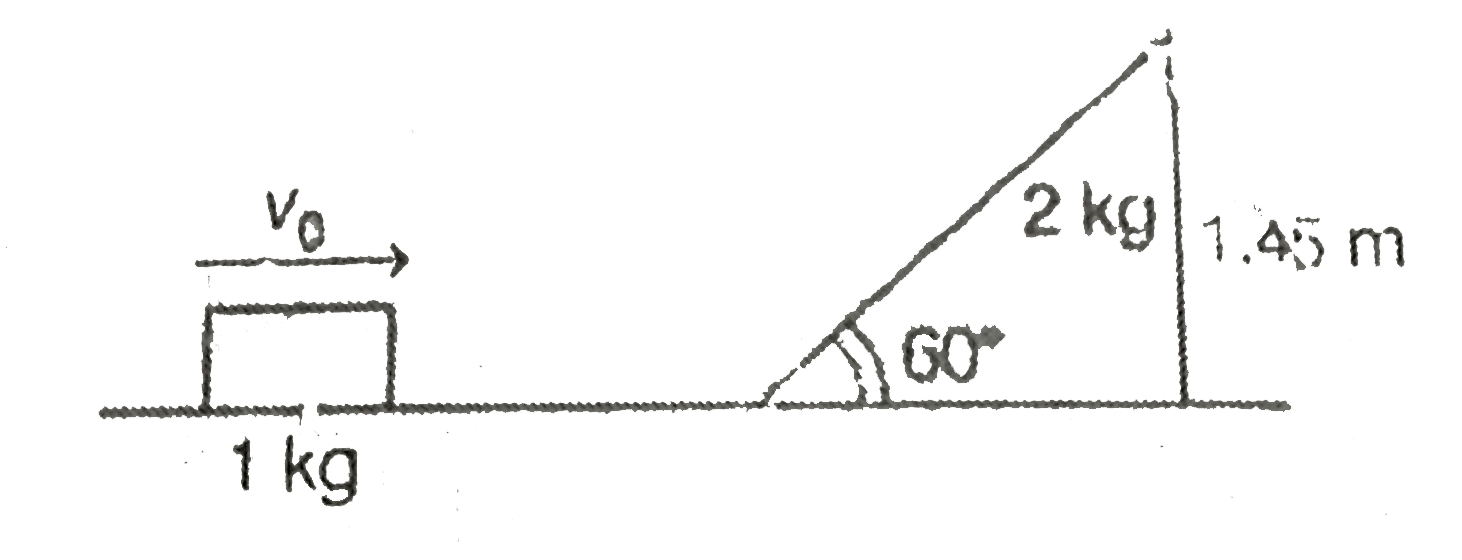
In the whole process let J be the magnitude of net impulse given to the block by the wedge, JH its horizontal component and JV its vertical component. Then
View SolutionA block of mass 1kg is pushed on a non-movable wedge of mass 2kg and height h=30cm with a velocity u=6m/sec. Before striking the wedge it travels 2m on a rough horizontal portion. Velocity is just sufficient for the block to reach the top of the wedge. Assuming all surfaces are smooth except the given horizontal part and collision of block and wedge is jerkless, the friction coefficition of the rough horizontal part is :
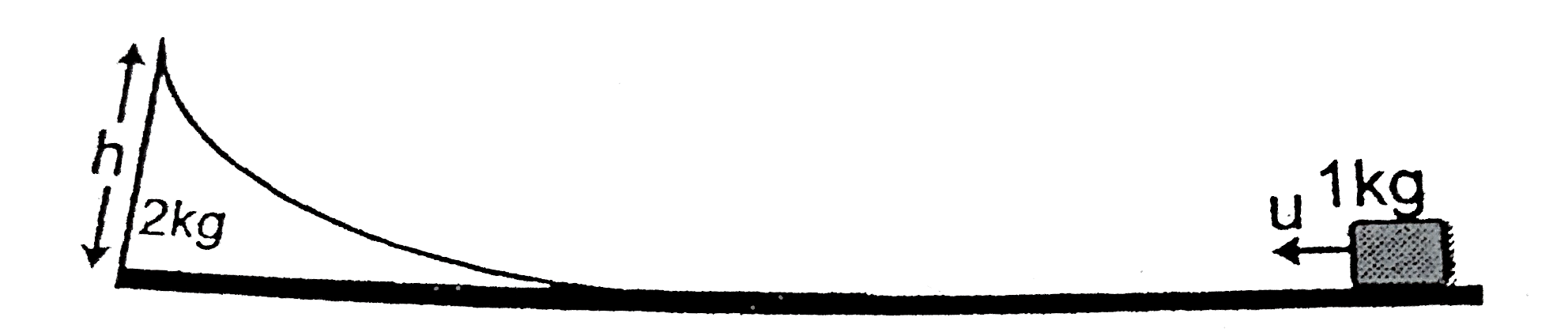
View SolutionA block of mass 1 kg is moving towards a movablen vedge of amss 2 kg as shown in figure. All surfaces are smooth. When the block leaves the wedge from top, its velocity is making an angle θ=30∘ with horizontal.

To what maximum height will the block rise
View SolutionA block of mass m is placed at rest on a smooth wedge of mass M placed at rest on a smooth horizontal surface. As the system is released

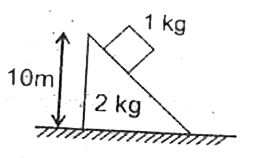
View SolutionA block of mass 1 kg is released from the top of a wedge of mass 2 kg. Height of wedge is 10 meter and all the surfaces are frictionless. Then
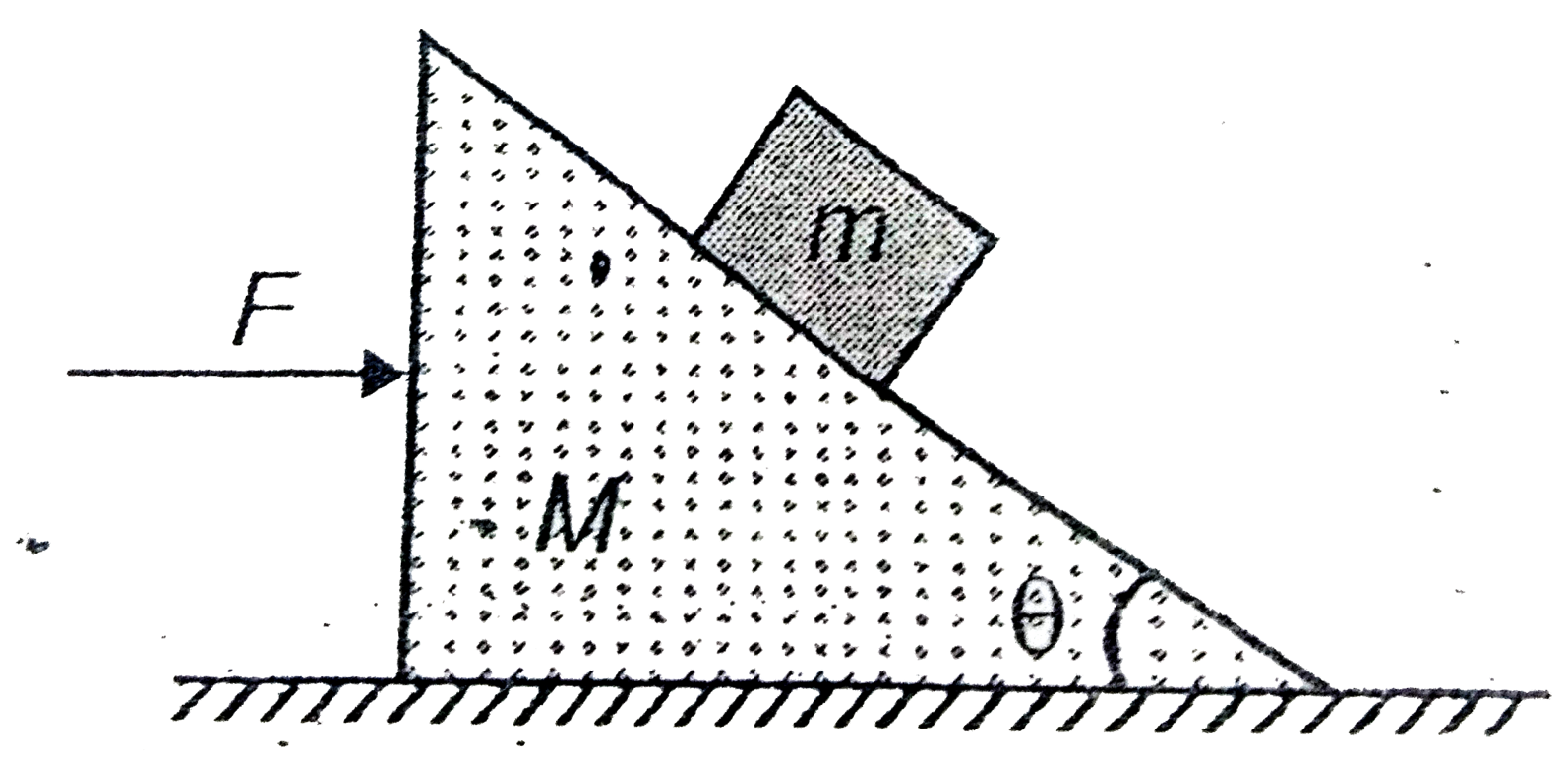
View SolutionA block of mass m is placed on a wedge of mass M and a force F is acting on its as shown . If all surfaces are smooth , find the force F such that, there is no relative motion between m and M.
View Solution
