The position of a paricle moving along x−axis depends on time as x=2(1−e−31). Choose the correct statement(s).
Total displacement of the particle is 2 units
Total distance covered by particle is 2 units.
Velocity of the particle will change its direction at some instant.
Velocity of particle will not change its direction throughout the motion.
The correct Answer is:A, B, D
To solve the problem, we need to analyze the position function given for the particle moving along the x-axis, which is:
x(t)=2(1−e−3t)
Step 1: Determine the initial position at t=0
Substituting t=0 into the position equation:
x(0)=2(1−e−3⋅0)=2(1−e0)=2(1−1)=2⋅0=0
Hint: The exponential function e0 equals 1, which simplifies the calculation.
Step 2: Determine the position as t→∞
Now, we need to find the position of the particle as time approaches infinity:
x(∞)=2(1−e−3⋅∞)=2(1−0)=2
Hint: As t increases, e−3t approaches 0, simplifying the expression.
Step 3: Calculate the velocity
The velocity v(t) is the derivative of the position function with respect to time:
v(t)=dxdt=ddt(2(1−e−3t))
Using the chain rule:
v(t)=2⋅0−2⋅(−3)e−3t=6e−3t
Hint: Remember that the derivative of ekt is kekt.
Step 4: Analyze the velocity
Since e−3t is always positive for all t≥0, it follows that:
v(t)=6e−3t>0for all t≥0
Hint: The exponential function is always positive, which indicates that the velocity does not change sign.
Step 5: Conclusion about displacement and distance
1. Total Displacement: The total displacement from t=0 to t=∞ is x(∞)−x(0)=2−0=2 units.
2. Distance Covered: Since the velocity is always positive, the distance covered is equal to the total displacement, which is also 2 units.
3. Direction of Velocity: Since the velocity is always positive, it does not change direction.
Final Statements
- The total displacement of the particle is 2 units.
- The distance covered by the particle is also 2 units.
- The velocity of the particle does not change direction at any instant.
Correct Statements:
- The total displacement of the particle is 2 units.
- The distance covered by the particle is 2 units.
- The velocity of the particle does not change direction.
2. Distance Covered: Since the velocity is always positive, the distance covered is equal to the total displacement, which is also 2 units.
- The distance covered by the particle is also 2 units.
- The velocity of the particle does not change direction at any instant.
- The total displacement of the particle is 2 units.
- The distance covered by the particle is 2 units.
- The velocity of the particle does not change direction.
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - TEST PAPERSEXERCISE - PHYSICS784videos
TEST PAPERS
- BOOK - RESONANCE ENGLISHCHAPTER - TEST PAPERSEXERCISE - PART - II PHYSICS SEC - 220videos
TEST PAPERS
- BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Advanced Level Problems13videos
SIMPLE HARMONIC MOTION
- BOOK - RESONANCE ENGLISHCHAPTER - TEST SERIESEXERCISE - PHYSICS130videos
TEST SERIES
Similar Questions
The position of a particle moving along x-axis varies eith time t as x=4t−t2+1. Find the time interval(s) during which the particle is moving along positive x-direction.
View Solution(a) The position of a particle moving along the x-axis depends on the time according to equation. x=(3t2−t3) m. At what time does the particle reaches its maximum x-position?
(b) What is the displacement during the first 4s.View SolutionThe position of a particle moving along x-axis is given by x=10t−2t2. Then the time (t) at which it will momentily come to rest is
View SolutionFor a particle moving along x-axis, a scaled x-6 graph is shown in figure. Mark the correct statement (s).
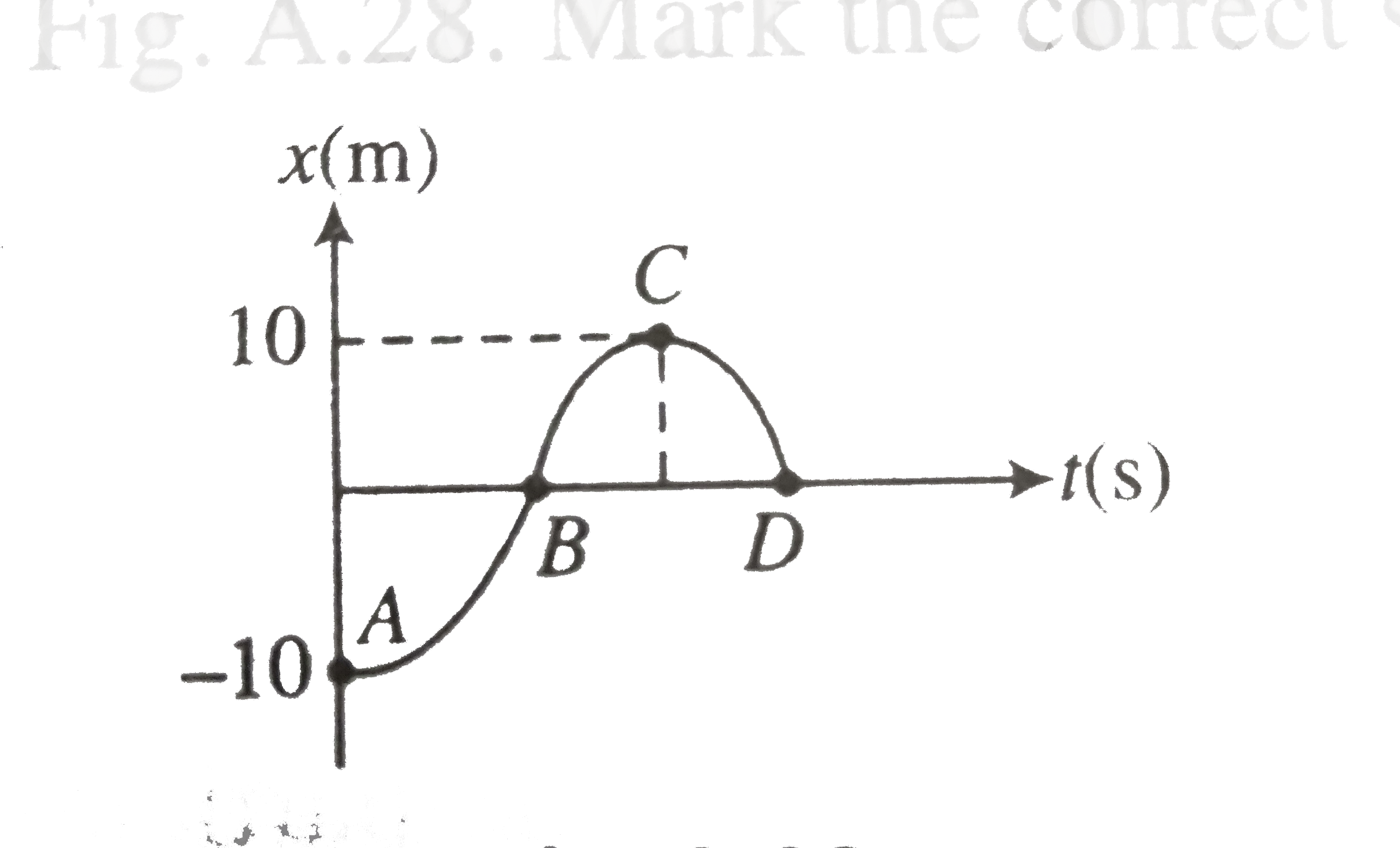 View Solution
View SolutionPosition of particle moving along x-axis is given as x=2+5t+7t2 then calculate :
View SolutionThe position of a particle moving along x- axis is given by x=x0cos2(ωt) . Its when it is at mean position is
View SolutionThe position (x) of a particle moving along x - axis veries with time (t) as shown in figure. The average acceleration of particle in time interval t = 0 to t = 8 s is
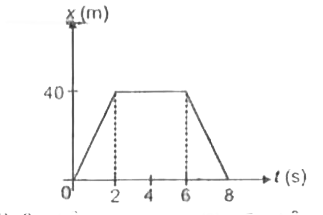 View Solution
View SolutionA particle is moving along the x-axis whose position is given by x=4−9t+t33. Mark the correct statement(s) in relation to its motion.
View SolutionFor a particle moving along the x-axis, x-t graph is as given as graph in figure. Mar the correct statement (s).
(#BMS_V01_MAA_E01_052_Q01.png" width="80%">View SolutionThe position x of particle moving along x-axis varies with time t as x=Asin(ωt) where A and ω are positive constants. The acceleration a of particle varies with its position (x) as
View Solution

