In the figure shown a thin light inextensible string is wrapped around a uniform disc. One end of the strin is fixed to the ceiling of the lift and the other end is fied to the circumference of the disc. Acceleration 'a' of the lift is such that the centre of the disc not move with respect to ground. Find the value of ag. String does not slip on pulley.
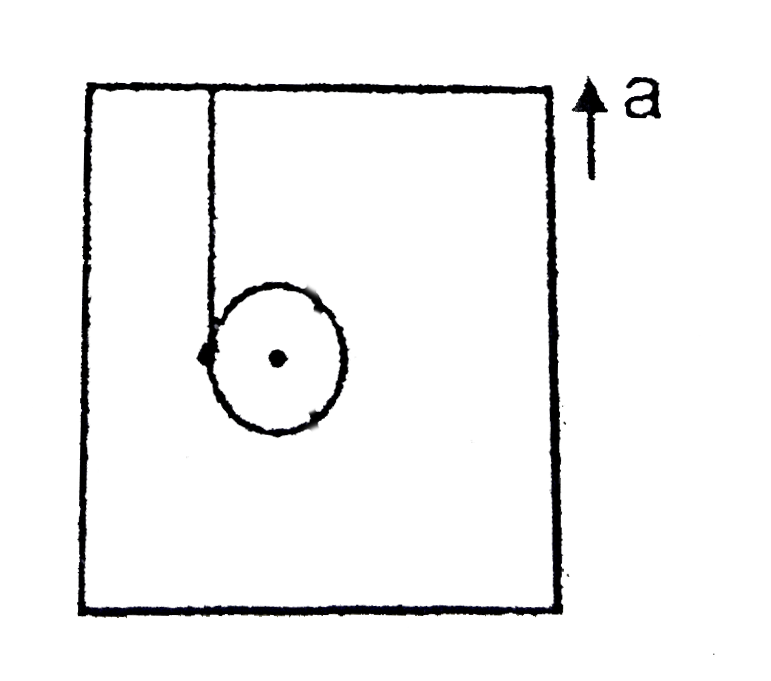
The correct Answer is:2
aA=a=α.R …….(i)
T−mg=0 ……(ii)
T.R=mR22.α………..(iii)
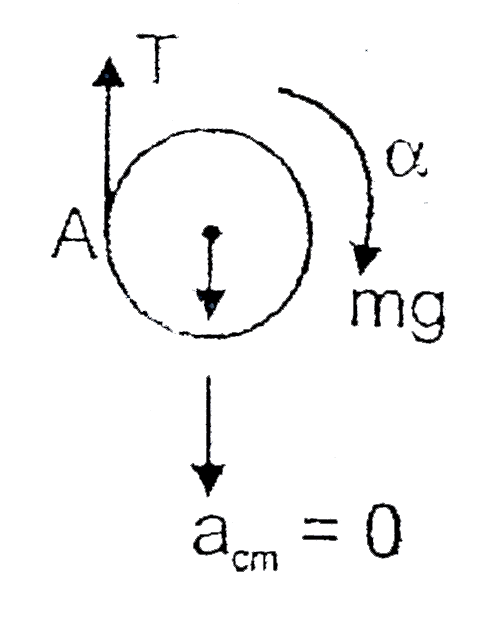
∴g=a2
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - TEST PAPERSEXERCISE - PHYSICS784videos
TEST PAPERS
- BOOK - RESONANCE ENGLISHCHAPTER - TEST PAPERSEXERCISE - PART - II PHYSICS SEC - 220videos
TEST PAPERS
- BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Advanced Level Problems13videos
SIMPLE HARMONIC MOTION
- BOOK - RESONANCE ENGLISHCHAPTER - TEST SERIESEXERCISE - PHYSICS130videos
TEST SERIES
Similar Questions
A string is wrapped over the edge a uniform disc and the free end is fixed with the ceiling. The disc moves down, unwinding the string. Find the downward acceleration of the disc.
View SolutionA disc of mass M has a light, thin string wrapped several times around its circumference. The free end of string is attaced to the ceiling and the disc is released from rest. Find the acceleration of the disc and the tension in the string.
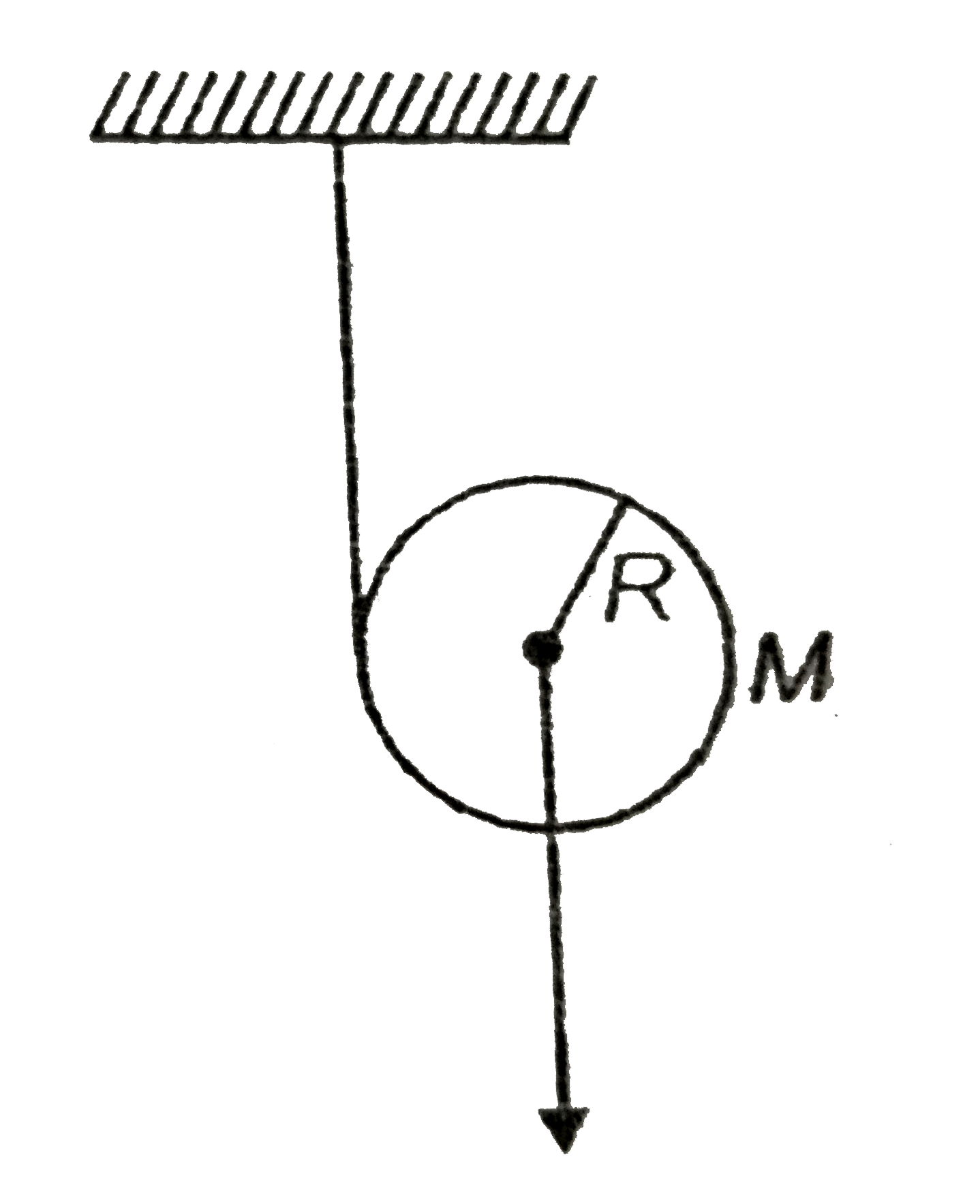View SolutionA string is wrapped on a uniform disc and the other end of the string connected to a wall. The system is placed on a smooth plane, inclined at an angle θ, with the string parallel to the plane, as shown in the figure. The acceleration of the disc is
View Solution
Consider the arrangement shown in figure. The string is wrapped around a uniform cylinder which rolls without slipping. The other end of the string is passed over a masslessm frictionless pulley to a falling weight, determine the acceleration of the falling mass m in terms of only the mass of the cylinder M, the mass m and gView SolutionOne end of a string of length L is tied to the celling of lift accelerating upwards with an accelerating 2g The other end of the string is free. The linear mass density of the string varies linearly from 0 of λ from bottom to top :-
View SolutionThe pulley shown in figure has a moment of inertia I about it's axis and its radius is R. Find the magnitude of the acceleration of the two blocks. Assume that the string is light and does not slip on the pulley.
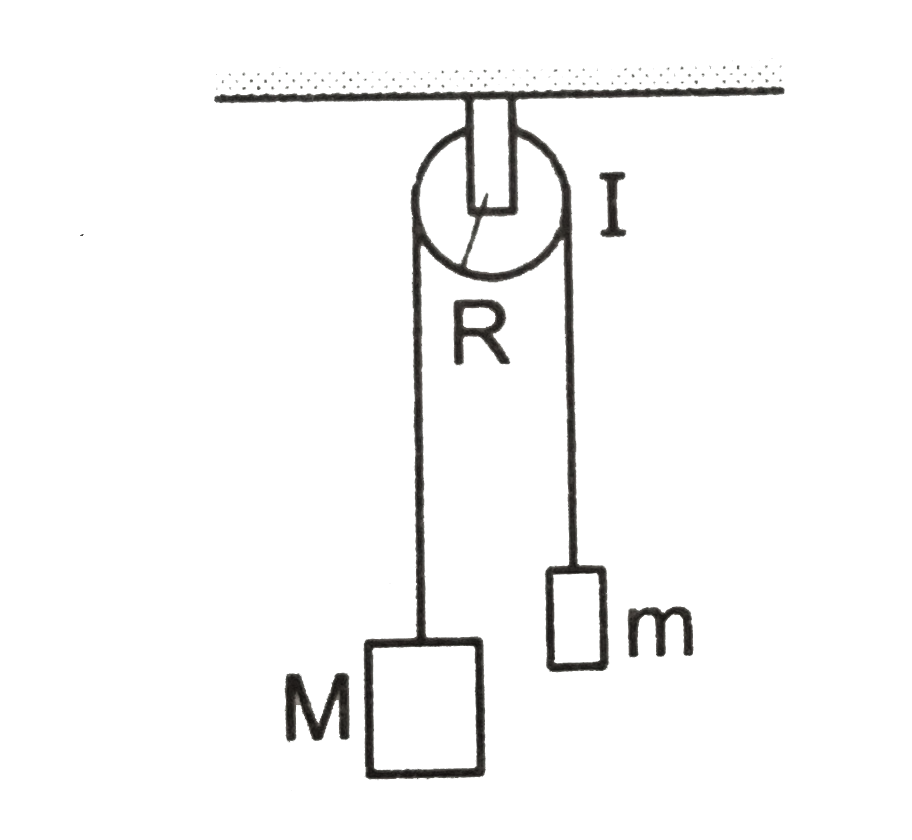View SolutionOne end of spring of spring constant k is attached to the centre of a disc of mass m and radius R and the other end of the spring connected to a rigid wall. A string is wrapped on the disc and the end A of the string (as shown in the figure) is pulled through a distance a and then released.
The disc is placed on a horizontal rough surface and there is no slipping at any contact point. What is the amplitude of the oscillation of the centre of the disc?
View SolutionA mas m hangs with help of a string wraped around a pulley on a frictionless bearling. The pulley has mass m and radius R. Assuming pulley to be a perfect uniform circular disc, the acceleration of the mass m, if the string does not slip on the pulley, is:
View SolutionA block of mass m is attached to one end of a light string which is wrapped on a disc of mass 2m and radius R. The total length of the slack portion of the string is l. The block is released from rest. The angular velocity of the disc just after the string becomes taut is
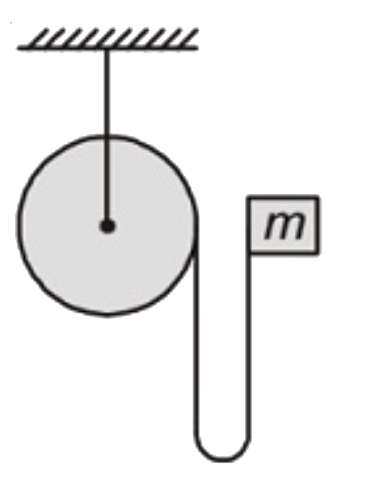View SolutionOne end of a string of length L is tied to the ceiling of a lift acceleration upwards with an acceleration 2g. The other end of the string is free. The linear mass density of the string varies linearly from 0→λ from bottom to top. Choose the correct option(s)
View Solution