If a pendulum swings with the same period at the top of the mountain and at the bottom of the mine then the ratio between height H of a mountain and the depth h of a mine is :
12
1
14
2
The correct Answer is:A
To solve the problem of finding the ratio between the height H of a mountain and the depth h of a mine when a pendulum swings with the same period at both locations, we can follow these steps:
Step 1: Understand the Period of a Pendulum
The period T of a simple pendulum is given by the formula:
T=2π√Lg
where L is the length of the pendulum and g is the acceleration due to gravity.
Step 2: Determine the Acceleration Due to Gravity
The acceleration due to gravity changes with height and depth. At a height H above the Earth's surface, the acceleration due to gravity g′ is given by:
g′=g(1−2HR)
where R is the radius of the Earth.
At a depth h below the Earth's surface, the acceleration due to gravity g′′ is given by:
g′′=g(1−hR)
Step 3: Set the Periods Equal
Since the pendulum swings with the same period at both locations, we can set the expressions for the periods equal:
2π√Lg′=2π√Lg′′
This simplifies to:
√Lg′=√Lg′′
Squaring both sides gives:
Lg′=Lg′′
Since L is the same for both cases, we can cancel it out:
g′=g′′
Step 4: Substitute the Expressions for g′ and g′′
Substituting the expressions for g′ and g′′:
g(1−2HR)=g(1−hR)
Step 5: Cancel g and Rearrange
Cancelling g from both sides (assuming g≠0):
1−2HR=1−hR
This simplifies to:
−2HR=−hR
Multiplying through by −R gives:
2H=h
Step 6: Find the Ratio Hh
From the equation 2H=h, we can express the ratio of H to h:
Hh=12
Conclusion
Thus, the ratio between the height H of the mountain and the depth h of the mine is:
Hh=12
The period T of a simple pendulum is given by the formula:
T=2π√Lg
where L is the length of the pendulum and g is the acceleration due to gravity.
The acceleration due to gravity changes with height and depth. At a height H above the Earth's surface, the acceleration due to gravity g′ is given by:
g′=g(1−2HR)
where R is the radius of the Earth.
g′′=g(1−hR)
Since the pendulum swings with the same period at both locations, we can set the expressions for the periods equal:
2π√Lg′=2π√Lg′′
This simplifies to:
√Lg′=√Lg′′
Squaring both sides gives:
Lg′=Lg′′
Since L is the same for both cases, we can cancel it out:
g′=g′′
Substituting the expressions for g′ and g′′:
g(1−2HR)=g(1−hR)
Cancelling g from both sides (assuming g≠0):
1−2HR=1−hR
This simplifies to:
−2HR=−hR
Multiplying through by −R gives:
2H=h
From the equation 2H=h, we can express the ratio of H to h:
Hh=12
Thus, the ratio between the height H of the mountain and the depth h of the mine is:
Hh=12
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.41
9 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.42
20 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.39
9 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)
19 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
Similar Questions
From the top of a building 15m high the angle of elevation of the top of tower is found to be 30∘. From the bottom of same building ; the angle of elevation of the top of the tower is found to be 60∘. Find the height of the tower and the distance between tower and building .
View SolutionGiven below is a bar graph showing the heights of six mountain peaks.
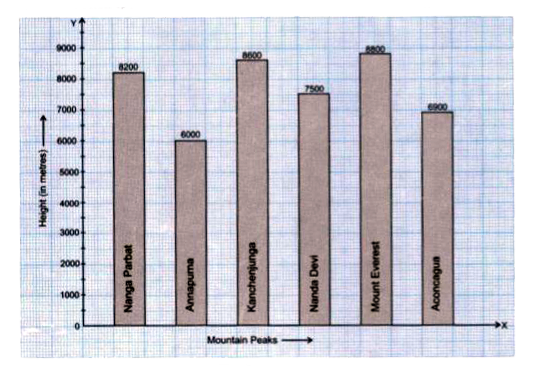
Read the above bar diagram and answer the following questions :
Find the ratio between highest and lowest mountain peak
View SolutionA pendulum clock, which keeps correct time at sea level, loses 15s per day when taken to the top of a mountain. If the radius of the earth is 6400km, the height of the mountain is
View SolutionFrom the bottom of a pole of height h, the angle of elevation of the top of a tower is α. The pole subtends an angle β at the top of the tower. find the height of the tower.
View SolutionFrom the bottom of a pole of height h, the angle of elevation of the top of a tower is α. The pole subtends an angle β at the top of the tower. find the height of the tower.
View SolutionFollowing is a bar graph giving the approximate heights of five mountain peaks. Read the graph and answer the following questions.
Find the ratio of the height of the highest peak to that of the lowest peak.

View Solution(Figure 5.11) shows two positions AandB at the same height h above the ground. If the maximum height os the projectile is H, then determine the time t elapses between the positions AandB in terms of H.
 .
.
View SolutionAt the top of a mountain a thermometer reads 70C and barometer reads 70cm of Hg. At the bottom of the mountain the barometer reads 76cm of Hg and thermometer reads 270C. The density of air at the top of mountain is "_" times the density at the bottom.
View SolutionIf g is same at a height h and at a depth d, then
View SolutionA body starts rolling down an inclined plane of length L and height h. This body reaches the bottom of the plane in time t. The relation between L and t is?
View Solution
