A sphere of radius is projected with a reverse spin down a rough inclined plane with a speed for which coefficient of friction is , where is angle of the inclination. Show that it will turn back if

Hence, the sphere will turn back if at the moment its centre of mass comes to stop it must have angular speed in same direction as has.
Let at time ,
.....()
further , .....()
From Eq. () and (), we get
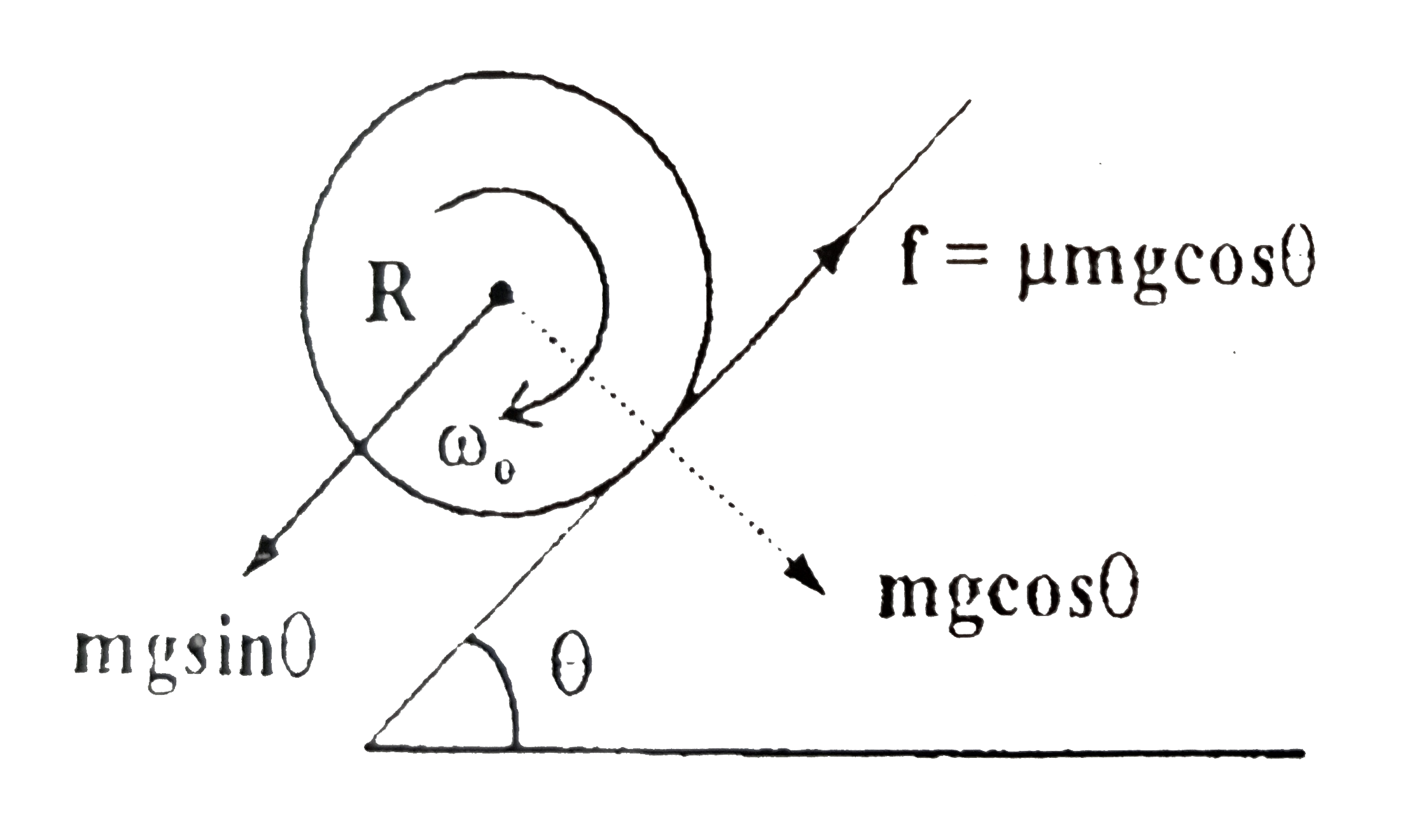
Topper's Solved these Questions
Similar Questions
Knowledge Check
A ring of radius R is rotating with an angular speed ω0 about a horizontal axis. It is placed on a rough horizontal table. The coefficient of kinetic friction is μk. The time after it starts rolling is.
AωoμkR2gBωog2μkRC2ωoRμkgDωoR2μkg
A cylinder of mass m radius R is spined to a clockwise angular velocity ωo and then gently placed on an inclined plane for which coefficient of friction μ=tanθ,θ is the angle of inclined plane with the horizontal. The centre of mass of cylinder will remain stationary for time

View SolutionA sphere is projected up an inclined plane with a velocity v0 and zero angular velocity as shown. The coefficient of friction between the sphere and the plane is μ=tanθ.. Find the total time of rise of the sphere.
View SolutionA block slides down an inclined plane that makes an angle θ with the horizontal. If the coefficient of kinetic friction is μ, find the acceleration of the block.
View SolutionA particle is projected with a speed v0=√gR. The coefficient of friction the particle and the hemi- spherical plane is μ=0.5 Then , the acceleration of the partical is
View SolutionThe force required to just move a body up the inclined plane is double the force required to just prevent the body from sliding down the plane. The coefficient of friction is μ. If θ is the angle of inclination of the plane than tanθ is equal to
View Solution
solid sphere of radius r is gently placed on a rough horizontal ground with an initial angular speed ω0 and no linear velocity. If the coefficient of friction is μ, find the time t when the slipping stops. in addition state the linear velocity v and angular velocity ω at the end of slipping
View SolutionA ring of mass m sliding on a smooth surface with velocity v0 enters rough surface with coefficient of kinetic friction μk, then
View Solution
