In the above question, the surface charge densities have the correct relation is-
A. σA>σB>σC>σD
B. σA=σB=σC=σD
C. σD>σC>σB>σA
D. σC<σB>σA>σD
σA>σB>σC>σD
σA=σB=σC=σD
σD>σC>σB>σA
σC<σB>σA>σD
The correct Answer is:A
To solve the problem regarding the surface charge densities on different parts of a conductor, we will analyze the relationship based on the geometry of the surfaces involved.
1. Identify the Surfaces:
We have four surfaces on the conductor:
- Surface A: Pointed end
- Surface B: Small semicircle
- Surface C: Long semicircle
- Surface D: Flat surface
2. Understand the Geometry:
- The radius of curvature for each surface is different:
- Surface A (pointed) has the smallest radius of curvature.
- Surface B (small semicircle) has a larger radius than A but smaller than C.
- Surface C (long semicircle) has a larger radius than B.
- Surface D (flat surface) has an infinite radius of curvature.
3. Apply the Concept of Charge Density:
- The surface charge density (σ) is inversely proportional to the radius of curvature (R). This means:
σ∝1R
- Therefore, the smaller the radius of curvature, the higher the surface charge density.
4. Establish the Relationships:
- Since Surface A has the smallest radius, it will have the highest charge density:
σA>σB>σC>σD
- This implies:
- σA (pointed end) > σB (small semicircle) > σC (long semicircle) > σD (flat surface).
5. Select the Correct Option:
- Based on the relationships derived, we can conclude that the correct option is:
- A. σA>σB>σC>σD
Final Answer:
The correct relation of the surface charge densities is:
A. σA>σB>σC>σD
We have four surfaces on the conductor:
- Surface A: Pointed end
- Surface B: Small semicircle
- Surface C: Long semicircle
- Surface D: Flat surface
- The radius of curvature for each surface is different:
- Surface A (pointed) has the smallest radius of curvature.
- Surface B (small semicircle) has a larger radius than A but smaller than C.
- Surface C (long semicircle) has a larger radius than B.
- Surface D (flat surface) has an infinite radius of curvature.
- The surface charge density (σ) is inversely proportional to the radius of curvature (R). This means:
σ∝1R
- Therefore, the smaller the radius of curvature, the higher the surface charge density.
- Since Surface A has the smallest radius, it will have the highest charge density:
σA>σB>σC>σD
- This implies:
- σA (pointed end) > σB (small semicircle) > σC (long semicircle) > σD (flat surface).
- Based on the relationships derived, we can conclude that the correct option is:
- A. σA>σB>σC>σD
The correct relation of the surface charge densities is:
A. σA>σB>σC>σD
Topper's Solved these Questions
Similar Questions
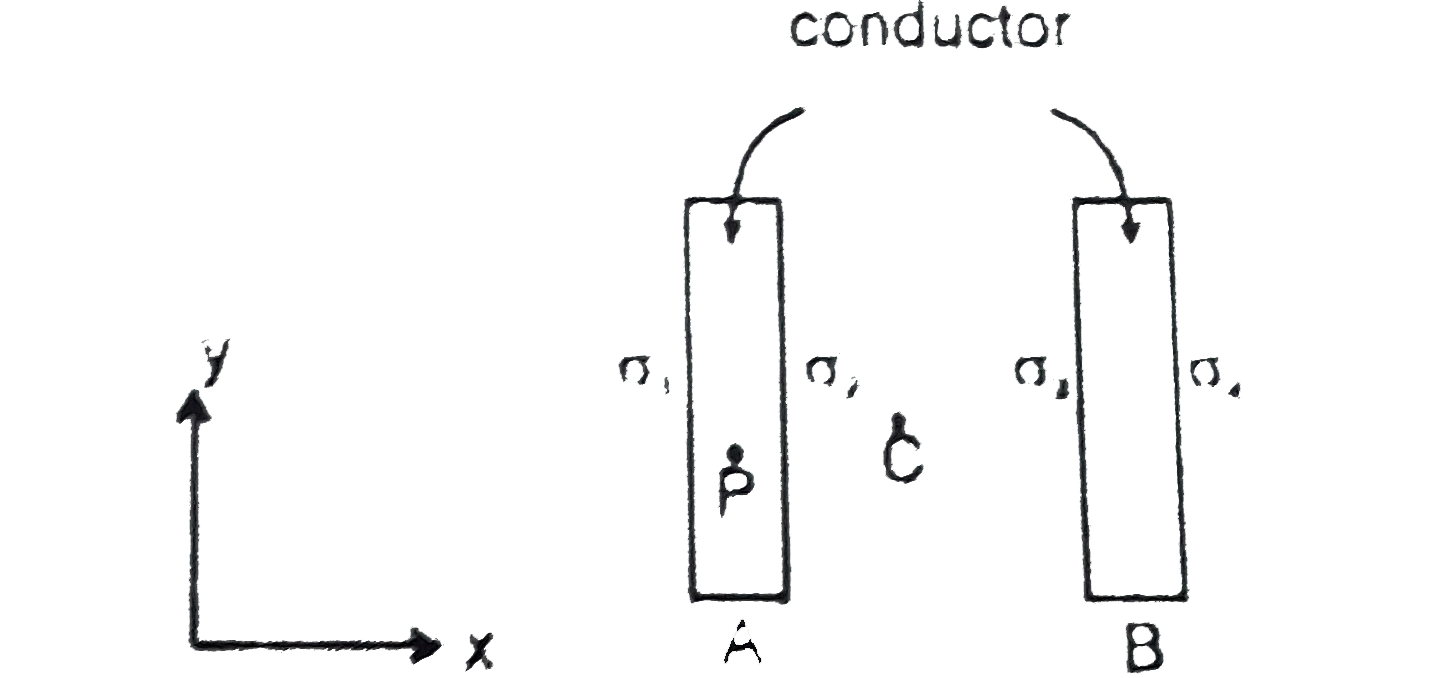
Figure shown two infinitely large conducting plates A and B. If electric field at C due to charge densities σ1,σ2,σ3 and σ40 is Eˆi, find σ2 and σ3 in terms of E. Derive a relation between σ1 and σ4.
View SolutionThe bond order for a species with the configuration σ1s2σ⋆1s2σ2s2σ∗2s2σ2px1 will be
View SolutionIf the standard deviation of a variable X is σ , then standard deviation of variable aX+bc is (a) aσ (b) acσ (c) ∣∣ac∣∣σ (d) aσ+bc
View SolutionIf the standard deviation of a variable X is σ , then standard deviation of variable aX+bc is (a) aσ (b) acσ (c) ∣∣ac∣∣σ (d) aσ+bc
View SolutionTwo paralle plane sheets 1 and 2 carry uniform charge densites σ1andσ2 (see fig. The electric field in the region marked I is (σ1>σ2):

View SolutionIn a sigma bond
View SolutionIf two variates X and Y are connected by the relation Y=aX+bc ,where a,b,c are constants such that ac<0,then (a) σγ=acσX (b) σγ=−acσX (c) σγ=acσX+b (d) none of these
View SolutionTwo parallel metallic plates have surface charge densities σ1 and σ2 as shown in figure.
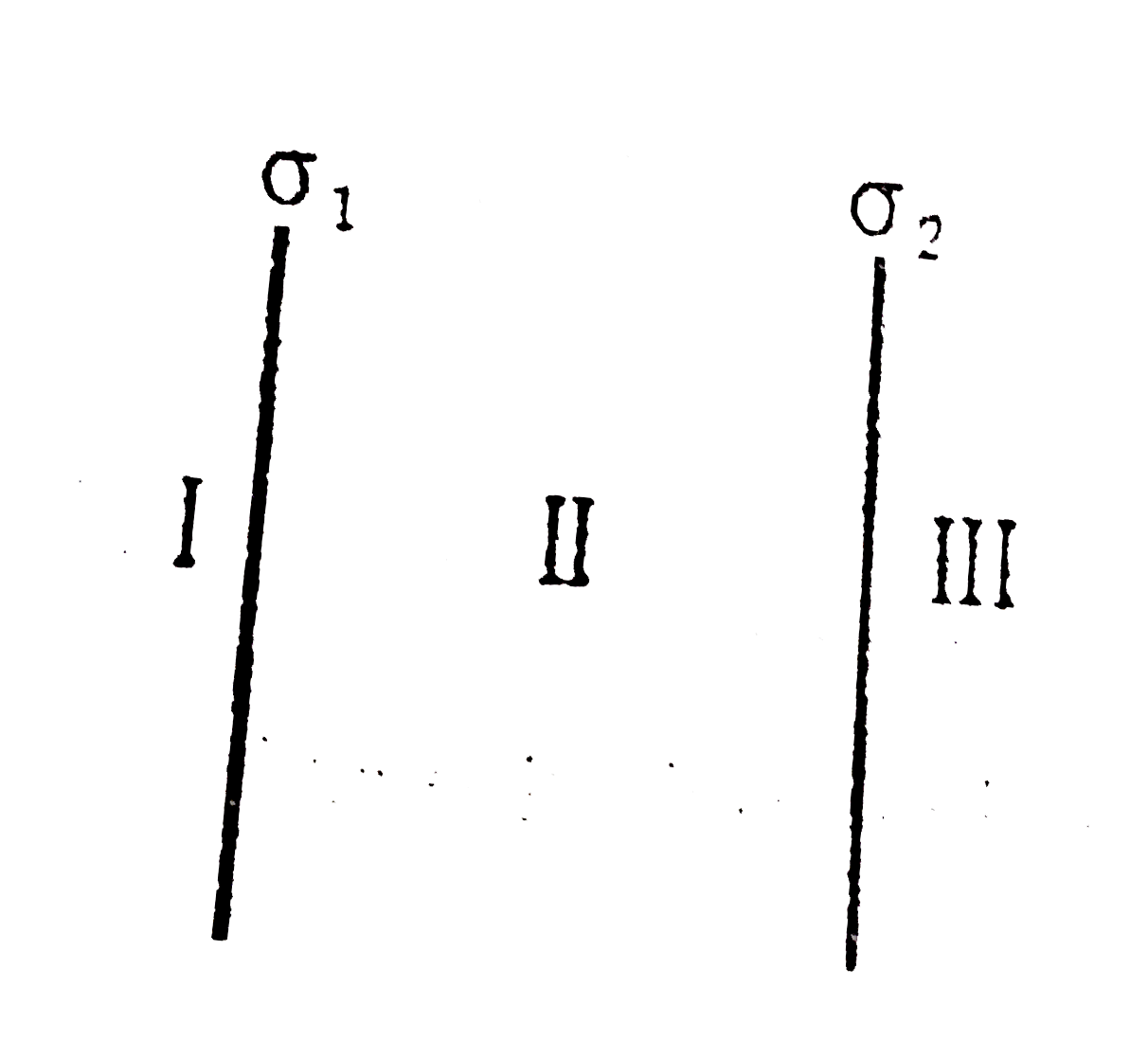
Column-IColumn-II(A)If σ1+σ2=0(p)Electric field in region III is towards right(B)Ifσ1+σ2>0(q)Electric field in region I is zero(C)If σ1+σ2<0(r)Electric field in region I is towards roght(s)Nothing can be said
View SolutionThe relation between voltage sensitivity 'σV' and current sensitiviy σi of moving coil galvanometer if its resistance is 'G' is
View SolutionIf Σnr=1cos−1xr=0,thenΣnr=1xr equals
View Solution
