
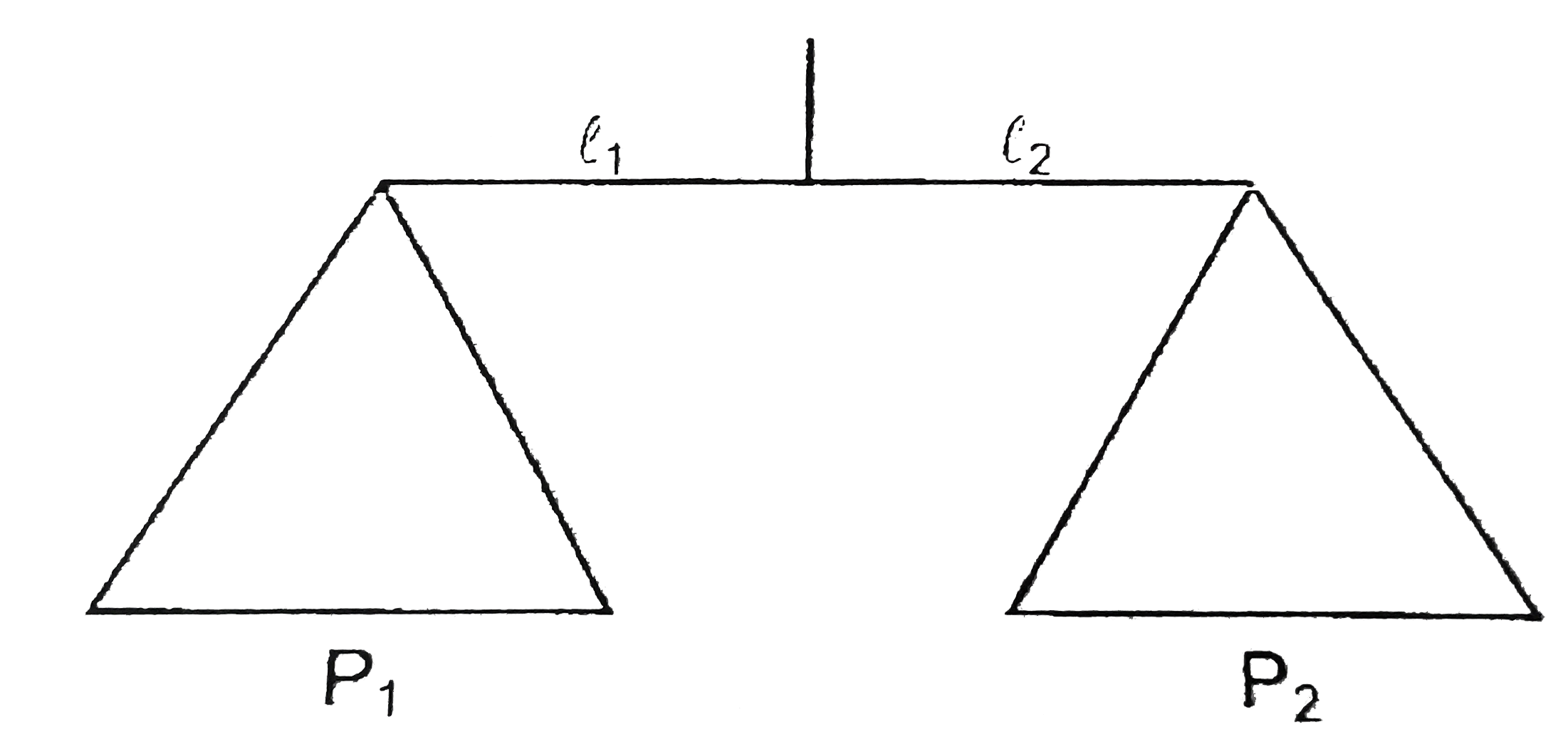
A true balance is one whose pans are of equal masses and arms are of equal lengths. When this happens, the net moment of forces about point of suspension is zero and beam remains horizontal without any weight i.e., for the true balance P1=P2 and l1=l2 also P1l1=P2l2 (mass of beam is neglibigle). A shopkeeper uses a false balance to weigh articles. Both arms and pans of this false balance are different, but beam become horizontal without any weight. (P1≠P2 and l1≠l2 but P1l1=P2l2).
Q. Shopkeeper use a weight W to weigh and article by false balance. in two weighing by using alternating pans let W1 and W2 are the weights of the article given to the customer i.e., customer gets (W1+W2) weight of article. Loss of gain to the shopkeeper is:
W(l2−l1)2l1l2 gain
W(l2−l1)2l1l2 loss
No gain, no loss
Data insufficient
The correct Answer is:B
Since P1l1=P2l2 and P2<P1⇒l2>l1
Wl1=W2l2⇒W2=Wl1l2 since l1l2<1⇒W2<W
⇒ there will be gain for shopkeeper
ΔW2=W−W2=W(l2−l1l2)
W1 be the weight of article when article put in P1
W1l1=Wl2⇒W1=Wl2l1 since l1l2<
⇒W1>W
⇒ there will be loss for shopkeeper
ΔW1=W1−W=W(l2−l1l1)
Since weight loss is more so net loss
=W(l2l1l1)−W(l2−l1l2)=W(l2−l1)2l1l2
Similar Questions
A true balance is one whose pans are of equal masses and arms are of equal lengths. When this happens, the net moment of forces about point of suspension is zero and beam remains horizontal without any weight i.e., for the true balance P1=P2 and l1=l2 also P1l1=P2l2 (mass of beam is neglibigle). A shopkeeper uses a false balance to weigh articles. Both arms and pans of this false balance are different, but beam become horizontal without any weight. (P1≠P2 and l1≠l2 but P1l1=P2l2).
Q. Choose the correct options(s)View SolutionA body weighs 6gms when placed in one pan and 24gms when placed on the other pan of a false balance. If the beam is horizontal when both the pans are empty, the true weight of the body is :
View SolutionThe two arms of a balanced are of unequal length. An object when placed in the left pan of the balance weighs 4 kg. The same object when placed in the right pan of the balance weighs 9 kg. The actual (or) true mass of the object is
View SolutionIn a beam balance, when the beam is balanced in horizontal position, it is in __________ equilibrium.
View SolutionThe length of a steel wire is l1 when the stretching force is T1 and l2 when the stretching force is T2. The natural length of the wire is
View SolutionTwo objects of equal mass rest on the opposite pans of an arm balance. Does the scale remain balance when it is accelerated up or down in a life ?
View SolutionA physical balance has its arms of length 60cm and 40cm. What weight kept on the pan of the longer arm will balance an object of weight 100 gf kept on the other pan?
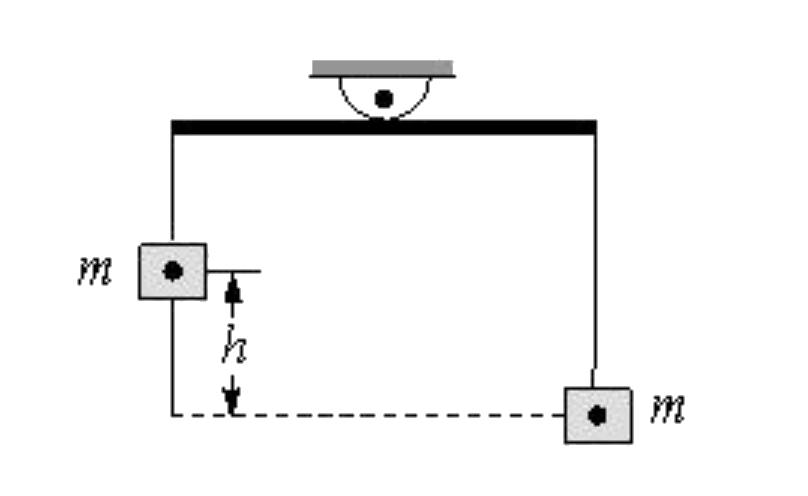
View SolutionTwo equal masses each in are hung from a balance whose scale pans differ in vertical height by h. The error in weighing in terms of density of the earth ρ is
View SolutionTwo equal masses each in are hung from a balance whose scale pans differ in vertical height by h. The error in weighing in terms of density of the earth ρ is
View SolutionTwo identical blocks of mass m are suspended from a beam balance whose scale pans differ in vertical height by h(h<<R), if R and ρ are the radius and density of the earth, then the error in weighing is
 View Solution
View Solution

