Two identical balls P and Q moving in the x−y plane collide at the origin (x=0,y=0) of the coordinate system. Their velocity components just before the moment of impact were, for ball P,vx=6m/s,vy=0,p for ball Q,vx=−5m/s,vy=2m/s
As a result of the collision, the ball P comes to rest. The velocity components of the ball Q just after collision will be:
vx=0
vy=2m/s
vy=3m/s
vx=1m/s
To solve the problem step-by-step, we will use the principle of conservation of momentum, which states that the total momentum before the collision is equal to the total momentum after the collision.
Step 1: Identify the initial velocities of the balls
- For ball P:
- vPx=6m/s
- vPy=0m/s
- For ball Q:
- vQx=−5m/s
- vQy=2m/s
Step 2: Calculate the initial momentum of both balls
The momentum of an object is given by the product of its mass and velocity. Since the balls are identical, we can denote their mass as m.
- Initial momentum of ball P:
Momentum of P=m⋅vPx+m⋅vPy=m(6)+m(0)=6m
- Initial momentum of ball Q:
Momentum of Q=m⋅vQx+m⋅vQy=m(−5)+m(2)=−5m+2m=−3m
- Total initial momentum:
Total Initial Momentum=6m−3m=3m
Step 3: Analyze the situation after the collision
After the collision, ball P comes to rest, which means its final velocity components are:
- v′Px=0m/s
- v′Py=0m/s
Let’s denote the final velocity components of ball Q as v′Qx and v′Qy.
Step 4: Apply conservation of momentum
According to the conservation of momentum:
Total Initial Momentum=Total Final Momentum
Thus,
3m=m(v′Px+v′Qx)+m(v′Py+v′Qy)
Since v′Px=0:
3m=m(0+v′Qx)+m(0+v′Qy)
This simplifies to:
3=v′Qx+v′Qy
Step 5: Calculate the final velocities
We need to find v′Qx and v′Qy. From the problem, we know that:
- The initial y-component of momentum for ball Q was 2m (since vQy=2m/s).
- After the collision, the y-component of momentum must be conserved.
Thus, we have:
0+2=0+v′Qy
This gives:
v′Qy=2m/s
Now substituting v′Qy back to find v′Qx:
3=v′Qx+2
Solving for v′Qx:
v′Qx=3−2=1m/s
Final Result
The velocity components of ball Q just after the collision are:
- v′Qx=1m/s
- v′Qy=2m/s
Summary
Thus, the final velocity components of ball Q after the collision are:
- v′Qx=1m/s
- v′Qy=2m/s
- For ball P:
- vPx=6m/s
- vPy=0m/s
- vQx=−5m/s
- vQy=2m/s
The momentum of an object is given by the product of its mass and velocity. Since the balls are identical, we can denote their mass as m.
Momentum of P=m⋅vPx+m⋅vPy=m(6)+m(0)=6m
Momentum of Q=m⋅vQx+m⋅vQy=m(−5)+m(2)=−5m+2m=−3m
Total Initial Momentum=6m−3m=3m
After the collision, ball P comes to rest, which means its final velocity components are:
- v′Px=0m/s
- v′Py=0m/s
According to the conservation of momentum:
Total Initial Momentum=Total Final Momentum
Thus,
3m=m(v′Px+v′Qx)+m(v′Py+v′Qy)
3m=m(0+v′Qx)+m(0+v′Qy)
This simplifies to:
3=v′Qx+v′Qy
We need to find v′Qx and v′Qy. From the problem, we know that:
- The initial y-component of momentum for ball Q was 2m (since vQy=2m/s).
- After the collision, the y-component of momentum must be conserved.
0+2=0+v′Qy
This gives:
v′Qy=2m/s
3=v′Qx+2
Solving for v′Qx:
v′Qx=3−2=1m/s
The velocity components of ball Q just after the collision are:
- v′Qx=1m/s
- v′Qy=2m/s
Thus, the final velocity components of ball Q after the collision are:
- v′Qx=1m/s
- v′Qy=2m/s
Topper's Solved these Questions
Similar Questions
The collision of two balls of equal mass takes place at the origin of coordinates. Before collision, the components of velocities are (vx=50cm−1 , vy=0) and (vx=−40cm−1 and vy=30cms−1. The first ball comes to rest after collision. The velocity (components vx and vy respectively) of the second ball are
View SolutionA glass ball collides with an identical ball at rest with v0=2 m/sec. If the coefficient of restitution of collision is e = 0.5, find the velocities of the glass balls just after the collision.
View Solution
Knowledge Check
Two identical balls A and B moving with velocities + 0.5 m/s and −0.3.m/s respectively collide head-on elastically. The velocities of the ball A and B after collision will be respectively
A+0.5m/sand+0.3m/sB−0.3m/sand+0.5m/sC + 0.3 m//s and + 0.5 m//sD−0.5m/sand+0.3m/s
Two smooth balls A and B, each of mass m and radius R, have their centre at (0,0,R) and (5R,-R,R) respectively, in a coordinate system as shown. Ball A, moving along positive x-axis, collides with ball B. Just before the collision, speed of ball A is 4m/s and ball B is stationary. The collision between the balls is elastic. Velocity of the ball A just after the collsion is
A. (ˆi+√3ˆj)m/s
B. (ˆi−√3ˆj)m/s
C. (2ˆi+√3ˆj)m/s
D. (2ˆi+2ˆj)m/s
View SolutionTwo identiacal balls A and B having velocities of 0.5 m/s and 0.3 m/s respectively collide elastically in one dimension. The velocities of B and A after the collision respectively will be
View SolutionA ball P is moving with a certain velocity v, collides head-on with another ball Q of same mass at rest. The coefficient of restitution is 1/4, then ratio of velocity of P and Q just after the collision is
View SolutionA glass ball collides with a smooth horizontal surface (xz plane) with a velocity V=ai−bj. If the coefficient of restitution of collision be e, the velocity of the ball just after the collision will be
View SolutionTwo identical balls AandB having velocity of 0.5m/sand−0.3m/s respectively collide elastically in one dimension. The velocities of BandA after the collision respectively will be
View SolutionA ball of mass m is attached to the lower end of a vertical string whose upper end is fixed. An identcial ball 'B' moving with a velocity v0=6m/s at an angle θ=45∘ from vertical collides elastically with the ball 'A' as shown.
The verocity of the ball 'B' just after collision is
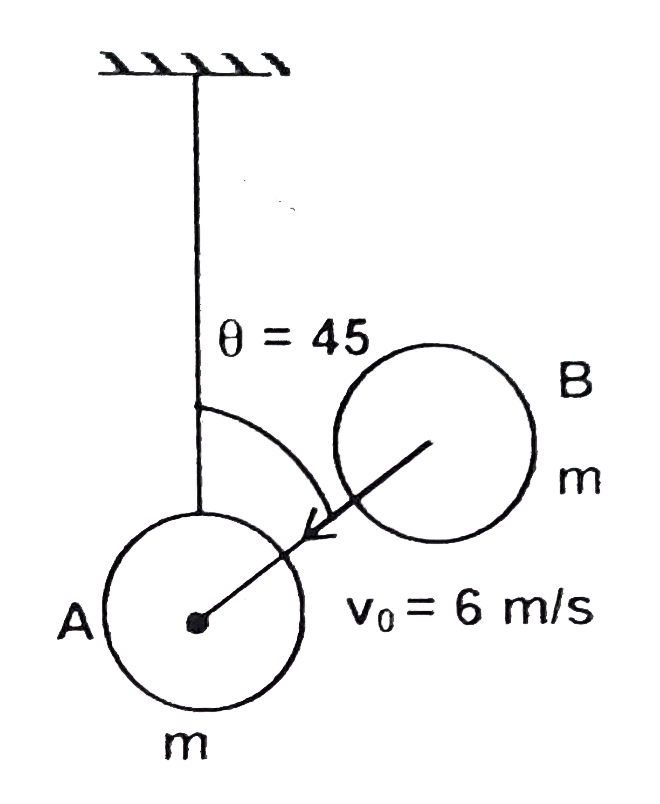
View SolutionTwo balls of masses m and 2m moving in opposite directions collide head on elastically with velocities v and 2v. Find their velocities after collision.
View Solution