A prism shaped styrofoam of density ρstyrofoam(<ρwater) is held completely submerged in water. It lies with its base horizontal. The base of foam is at depth h0 below water surface and atmospheric pressure is P0 Surface of water is open to atmosphere. Styrofoam prism is held in equilibrium by the string attached symmetrically as shown (Take ρstyrofoam=ρf,ρwater=ρw).
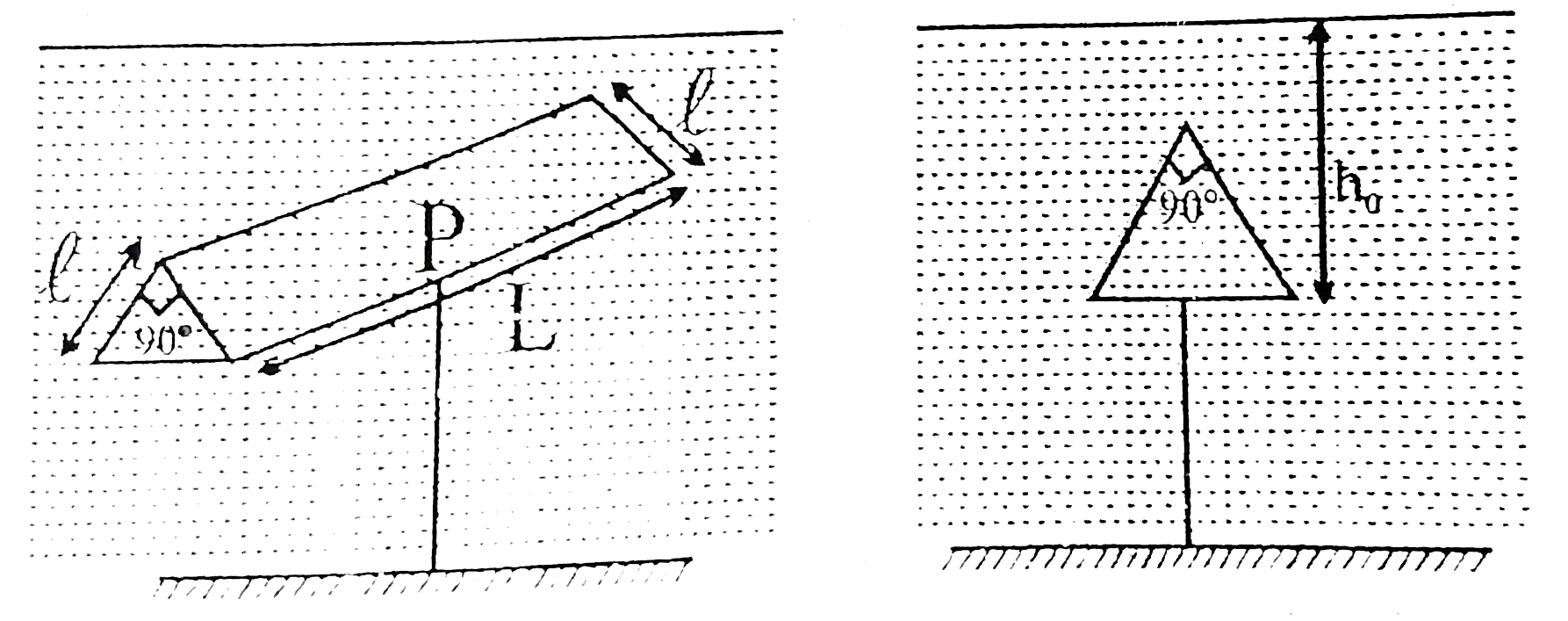
Net force exerted by liquid on the styrofoam is
√2ρgL2l
2ρgL2l
ρg(L2l)2
ρg(l2L)2
NA
Topper's Solved these Questions
Similar Questions
A prism shaped styrofoam of density ρstyrofoam(<ρwater) is held completely submerged in water. It lies with its base horizontal. The base of foam is at depth h0 below water surface and atmospheric pressure is P0 Surface of water is open to atmosphere. Styrofoam prism is held in equilibrium by the string attached symmetrically as shown (Take ρstyrofoam=ρf,ρwater=ρw).

Magnitude of force on any one of the slant face of styrofoam is
View SolutionAn air bubble of radius r in water is at a depth h below the water surface at some instant. If P is atmospheric pressure, d and T are density and surface tension of water respectively . the pressure inside the bubble will be :
View Solution
Knowledge Check
The pressure at depth h below the surface of a liquid of density ρ open to the atmosphere is
Agreater than the atmospheric pressure by ρghBless than the atmospheric pressure by ρghCequal to the atmospheric pressureDincreases exponentially with depthThe density of water at the surface of ocean is ρ . If the bulk modulus of water is B, then the density of ocean water at depth, when the pressure at a depth is αp0 and p0 is the atmospheric pressure is
AρKk−nP0BρKK+nP0CρKK−(n−1)P0DρK(K+(n−1)P0)
A small air bubble of radius 'r' is at a depth 'h' below the water surface (density of water=ρ). Surface tension of water is T, atmospheric pressure is p0. Find pressure inside the air bubble for the condition r<<h
View SolutionThe absolute pressure at a depth h below the surface of a liquid of density ρ is [Given Pa = atmospheric pressure, g = acceleration due to gravity]
View SolutionA beaker containing a liquid of density ρ moves up with an acceleration a. The pressure due to the liquid at a depth h below the free surface of the liquid is.
View SolutionWhen unit mass of water boils to become steam at 100∘C, it absorbs Q amount of heat. The densities of water and steam at 100∘C are ρ1 and ρ2 respectively and the atmospheric pressure is P0. The increase in internal energy of the water is
View SolutionDensity of a liquid varies with depth as ρ=αh. A small ball of density ρ0 is released from the free surface of the liquid. Then
View SolutionA small ball of density rho_(0) is released from the surface of a liquid whose density varies with depth h as ρ=ρ02(α+βh). Mass of the ball is m. Select the most appropriate one option.
View Solution
