If λ1,λ2andλ3 are the wavelengths of the wave giving resonance with the fundamental, first and second overtones respectively of a closed organ pipe Then the ratio of wavelength λ1,λ2andλ3 is
1:2:3
1:3:5
1:1/2:1/3
1:1/3:1/5
The correct Answer is:C
n1:n2:n3=1:2:3
Vλ1:Vλ2:Vλ3=1:2:3
λ1:λ2:λ3=1:12:13
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - SOUND WAVESEXERCISE - Exercise- 2 PART - I24videos
SOUND WAVES
- BOOK - RESONANCE ENGLISHCHAPTER - SOUND WAVESEXERCISE - Exercise- 2 PART - II20videos
SOUND WAVES
- BOOK - RESONANCE ENGLISHCHAPTER - SOUND WAVESEXERCISE - Exercise- 1 PART - I34videos
SOUND WAVES
- BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise28videos
SIMPLE HARMONIC MOTION
- BOOK - RESONANCE ENGLISHCHAPTER - STRING WAVESEXERCISE - Exercise32videos
STRING WAVES
Similar Questions
If λ1,λ2andλ3 are the wavelength of the waves giving resonance to the fundamental, first and second overtone modes respectively in a string fixed at both ends. The ratio of the wavelengths λ1:λ2:λ3 is
View SolutionIf I1,I2andI3 are wave lengths of the waves giving resonance with fundamental, first and second over tones of closed organ pipe. The ratio of wavelengths I1:I2:I3 is.....
View Solution
Knowledge Check
- Question 1 - Select One
If alpha particle, proton and electron move with the same momentum, them their respective de Broglie wavelengths λα,λp,λe are related as
Aλα=λp=λeBλα<λp<λeCλα>λp>λeDλp>λe>λα
If λ1andλ2 are the wavelength of the first members of the Lyman and Paschen series, respectively , then λ1:λ2 is
View SolutionIf λ1 and λ2 are the wavelengths of the first members of the Lyman and paschen series respectively, then λ1λ2 is equal to
View Solutionif λv',λx and λm represent the wavelengths of visible light X-rays and microwaves respectively then:
View Solutionif λv',λx and λm represent the wavelengths of visible light X-rays and microwaves respectively then:
View Solution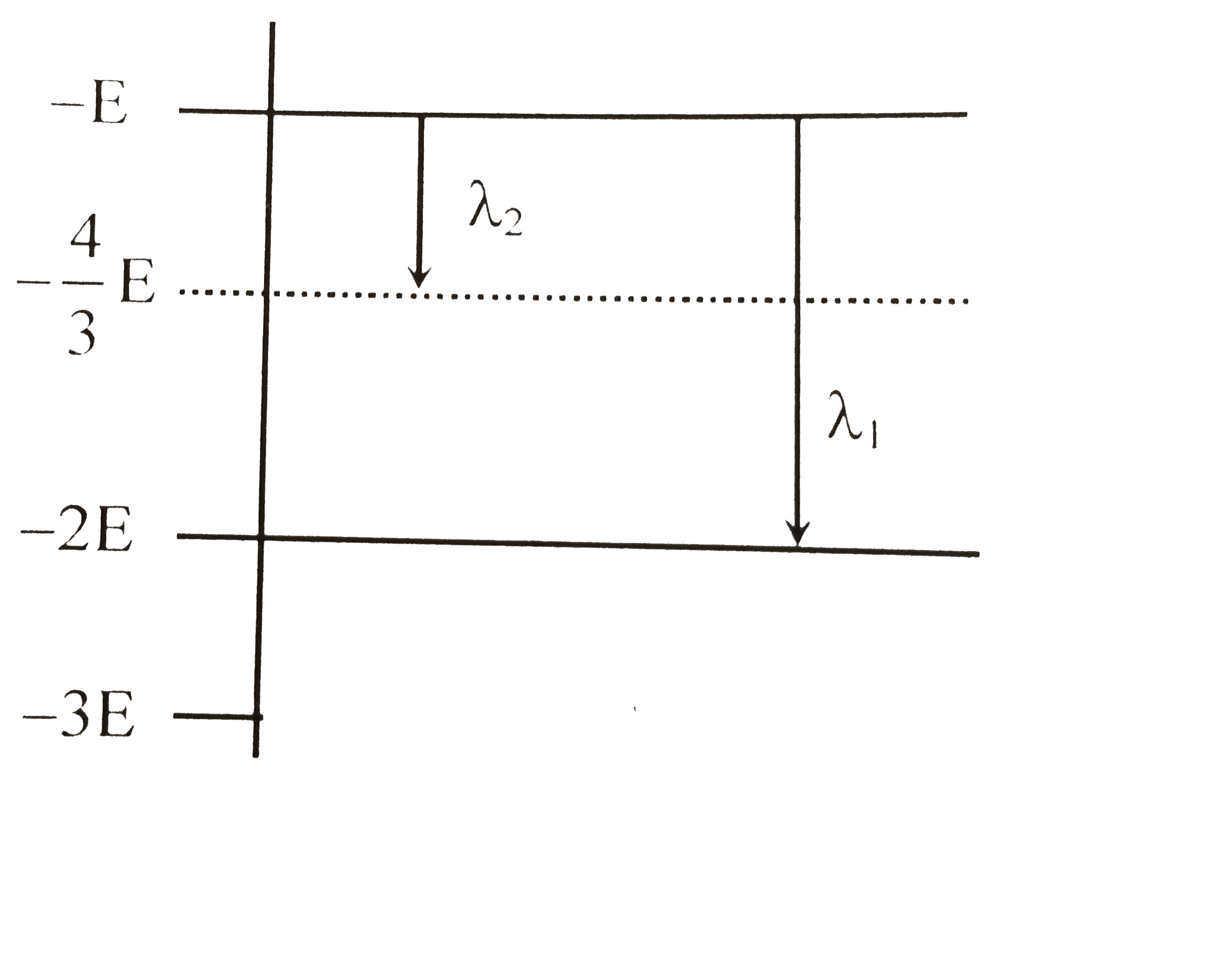
Some energy levels of a molecule are shown in the figure. The ratio of the wavelength r=λ1λ2,is given by:View SolutionThe ration of resolving powers of an optical microscope for two wavelangths
λ1=4000 Åandλ2=6000ÅisView SolutionIf λ1 and λ2 denote the wavelength of de Broglie waves for electrons in the first and second Bohr orbits in a hydrogen atom, the λ1λ2 is equal to
View Solution

