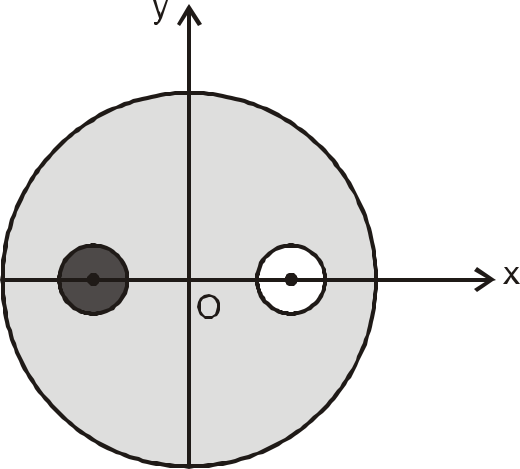
Consider a solid sphere of density ρ and radius 4R. Centre of the sphere is at origin. Two spherical cavities centered at (2R, 0) and (–2R, 0) are created in sphere. Radii of both cavities is R. In left cavity material of density 2ρ is filled while second cavity is kept empty. What is gravitational field at origin.
4GρπR3
3GρπR2
GρπR3
2GρπR3
The correct Answer is:D
Above distribution canbe represented as shown in figure
Gravitation field due to sphere of radius R at a distance 2R. 
Eg=Gρ43πR34R2=GρπR3
So net field at centre will be2Fg=2GρπR3
Topper's Solved these Questions
Similar Questions
A solid sphere having uniform charge density ρ and radius R is shown in figure. A spherical cavity ofradius R2 is made in it. What is the potential at point O?
View SolutionA solid sphere of uniform density and radius 4 units is located with its centre at the origin O of coordinates. Two sphere of equal radii 1 unit, with their centres at A(-2,0 ,0) and B(2,0,0) respectively, are taken out of the solid leaving behind spherical cavities as shown if fig Then:
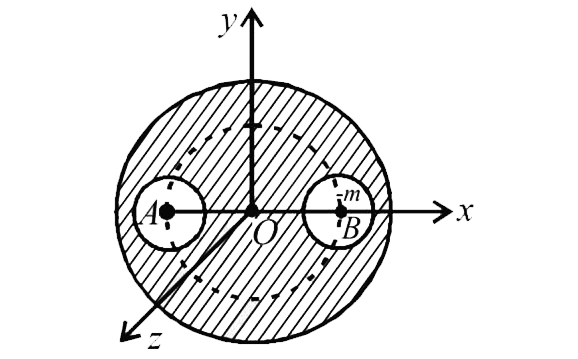
The gravitational field due to this object at the orgin is zero.
The gravitational force at point B(2, 0, 0) is zero.
The gravitational force at point B(2, 0, 0) is zero.
Both (1) & (3)View Solution
Knowledge Check
- Question 1 - Select One
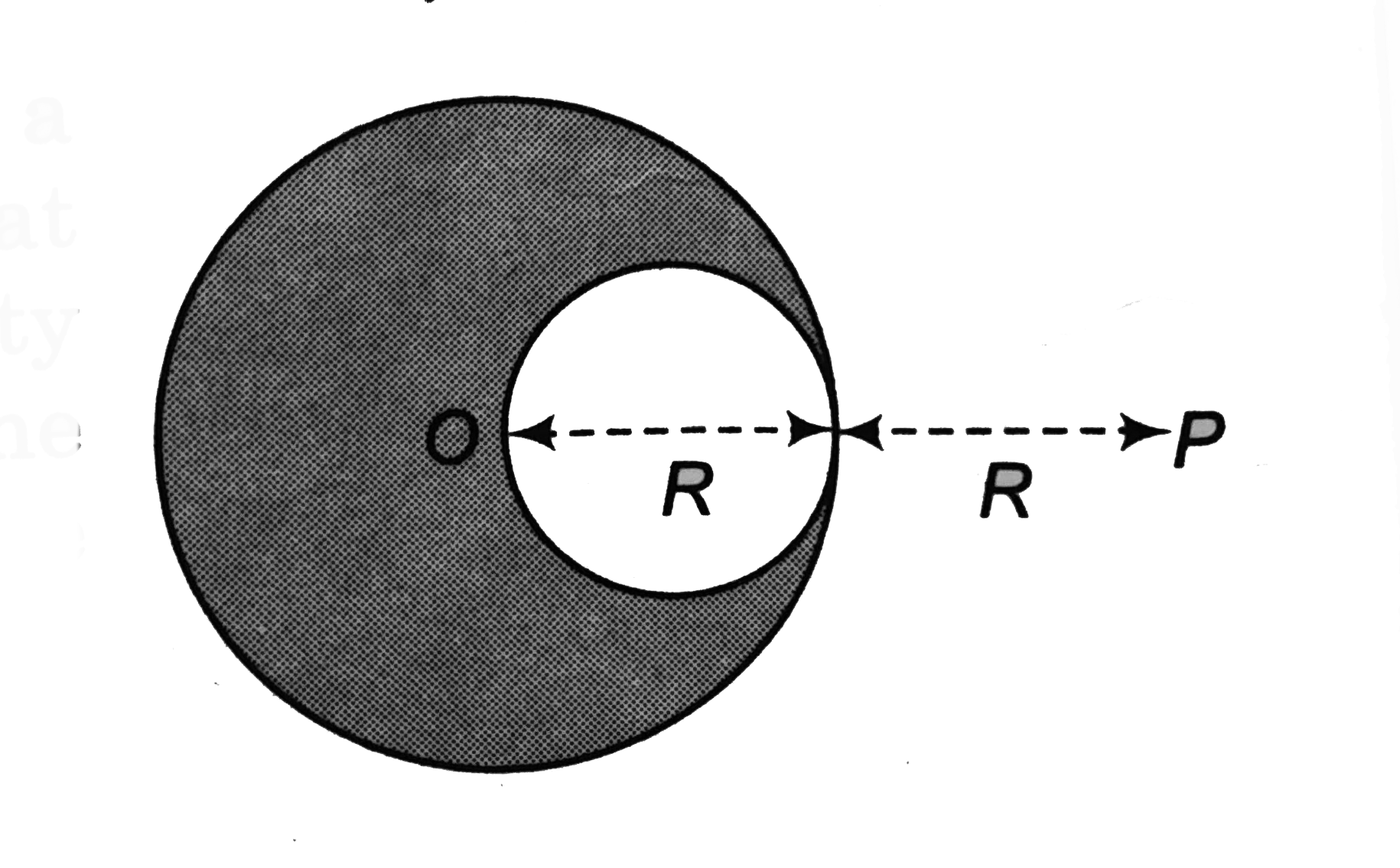
A solid sphere of uniform density and radius R applies a gravitational force of attraction equal to F1 on a particle placed at P, distance 2R from the centre O of the sphere. A spherical cavity of radius R/2 is now made in the sphere as shown in figure. The particle with cavity now applies a gravitational force F2 on same particle placed at P. The radio F2/F1 will be
A1/2B7/9C3D7
A solid sphere of uniform density and radius 4 units is located with its centre at the origin O of coordinates. Two sphere of equal radii 1 unit, with their centres at A(-2,0 ,0) and B(2,0,0) respectively, are taken out of the solid leaving behind spherical cavities as shown if fig Then:
View SolutionA solid sphere of uniform density and radius 4 units is located with its centre at the origin O of coordinates. Two sphere of equal radii 1 unit, with their centres at A(-2,0 ,0) and B(2,0,0) respectively, are taken out of the solid leaving behind spherical cavities as shown if fig Then:
View SolutionThe figure represents a solid uniform sphere of mass M and radius R. A spherical cavity of radius r is at a distance a from the centre of the sphere. The gravitational field inside the cavity is
View SolutionA hemi-spherical cavity is created in solid sphere (of radius 2R) as shown in the figure. Then
View SolutionA uniform solid sphere of radius R has a cavity of radius 1m cut from it if centre of mass of the system lies at the periphery of the cavity then
View SolutionA uniform solid sphere of radius R has a cavity of radius 1m cut from it if centre of mass of the system lies at the periphery of the cavity then
View SolutionA solid sphere of uniform density and radius R applies a gravitational force attraction equal to F1 on a particle placed at P, distance 2R from the centre O of the sphere. A spherical cavity of radius R/2 is now made in the sphere as shows in figure. The particle with cavity now applies a gravitational force F2 on same particle placed at P. The radio F2/F1 will be
View Solution