A semi circular disc of radius R is placed on a smooth horizontal surface. Figure shows top view of this. If temperature is increased by Δt then displacement of (coefficient of linear expansion is α): 
B along x-axis is RαΔt
B along y-axis is zero
A along y-axis isRαΔt
A along x- axis is −4R3παΔt
The correct Answer is:B, C, D
Displacement of centre of mass is zero. So take centre of mass as origin then find displacement of all points.
Topper's Solved these Questions
Similar Questions
A solid sphere of radius R is placed on a smooth horizontal surface. A horizontal force F is applied at height h from the lowest point. For the maximum acceleration of the centre of mass
View SolutionA solid sphere of radius R is placed on a smooth horizontal surface. A horizontal force F is applied at height h from the lowest point. For the maximum acceleration of the centre of mass
View Solution
Knowledge Check
- Question 1 - Select One
Length of wire at room temperature is 4.55 m , when the temperature increases upto 100∘C then its length becomes 4.57 m . The coefficient of linear expansion (α) of the given wire is
A5.021×10−5K−1B6.021×10−5K−1C7.021×10−5K−1D8.021×10−5K−1
A uniform metallic disc of radius r and mass m is spinning with angular speed ω0 about an axis passing through its centre and perpendicular to plane. If its temperature is increased (slightly) by ΔT its new angular speed is (The coefficient of linear expansion of the metal is α)
View Solution
A uniform circular disc of radius R is placed on a smooth horizontal surface with its plane horizontal and hinged at circumference through point O as shown . An impulse P is applied at a perpendicular distance h from its centre C. The value of h so that the impulse due to hinge is zero, isView SolutionA copper rod of length l0 at 0∘C is placed on smooth surface. Now, the rod is heated upto 100∘C. Find the longitudinal strain developed.
(α=coefficient of linear expansion)View SolutionA uniform circular disc of mass 'm' and radius 'R' is placed on a rough horizontal surface and connected to the two ideal non-deformed spring of stiffness k and 2k at the centre 'C' and point 'A' as shown . The centre of the disc is slighty displaced horizontally from equilibrium positon and then released, then the time period of small oscillation of the disc is (there is no slipping between the disc and the surface).
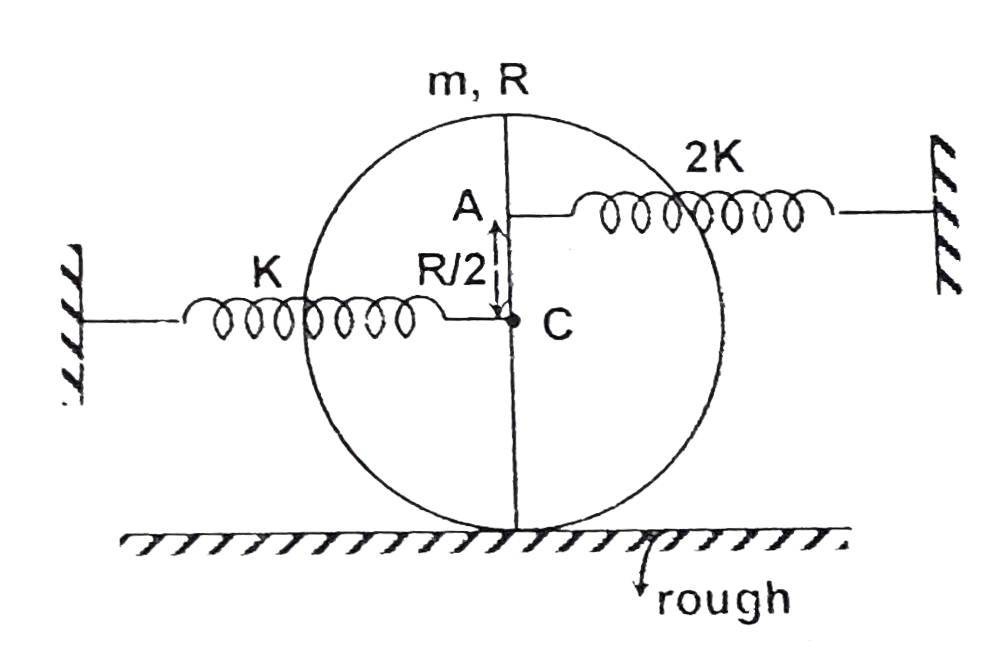View SolutionFigure shows a block A of mass 6m having a smooth semicircular groove of radius a placed on a smooth horizontal surface. A block B of mass m is released from a position in groove where its radius is horizontal. Find the speed of the bigger block when the smaller block reaches its bottom most position.
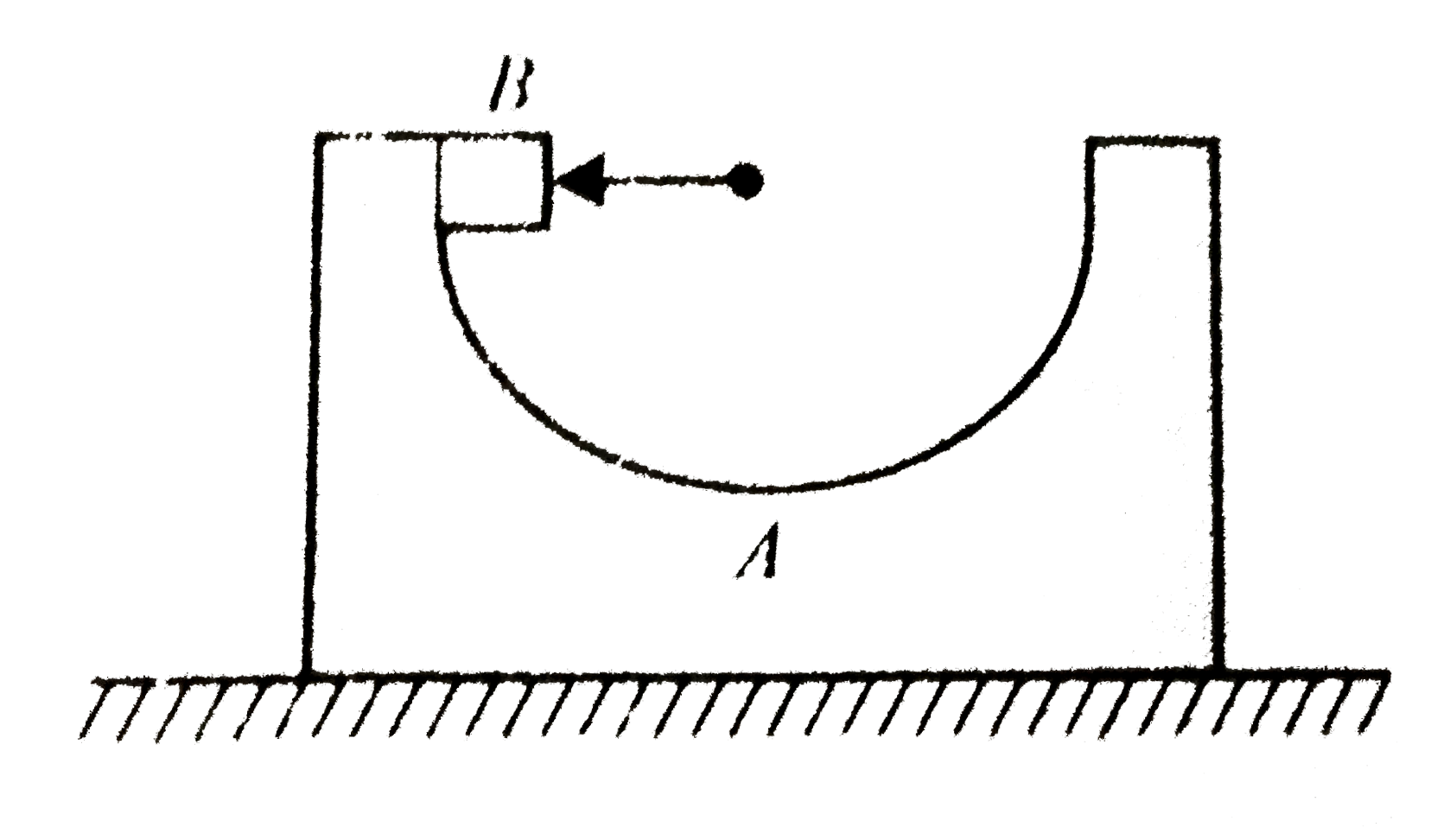View SolutionA disc having radius r=2m is placed on smooth horizontal surface. Velocity of point A and B is given as shown in fig. Distance between point O and axis of rotation at the particular instant is
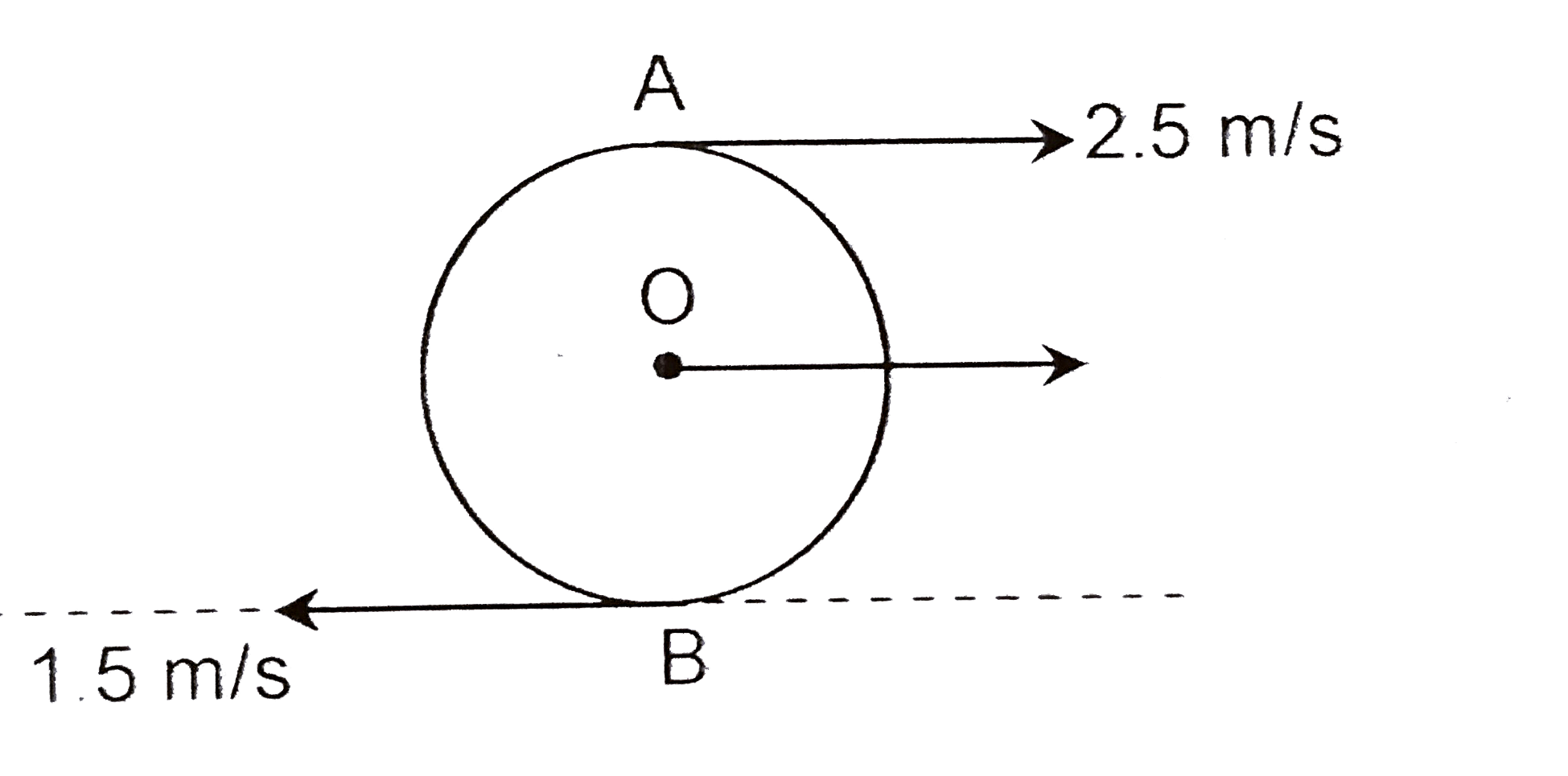View SolutionA uniform circular disc of mass 2 m and radius R placed freely on a horizontal smooth surface as shown in the figure- 5.116.A particle of mass m is connected to the circumference of the disc with a massless string. Now an impulse J is applied on the particle in the directions shown by dotted line. The acceleration of centre of mass of the disc just after application of implues is (If J =10N−sec.,m=√10kgandR=25cm)
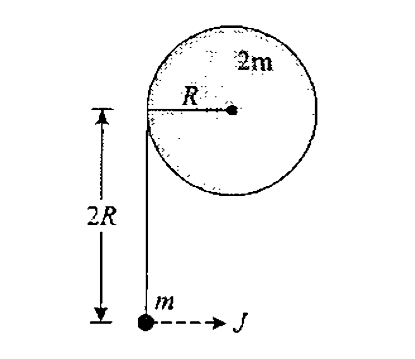View Solution