We have a thin spherical of radius R. Half of the sphere carrying surface change density σ1 and rest half carrying σ2. Magnitude of force of electromagnetic interaction between hemispherical parts carrying surface charge density σ1 and rest of the hemispherical portion is f0=α×104 Newton. Here α is an integer. Value of α will be.
Given σ1√ε0×102cm/m2,σ2=4σ1,R=√3πm
3
4
5
6
The correct Answer is:D
To solve the problem, we need to calculate the electromagnetic interaction force between two hemispherical parts of a sphere with different surface charge densities. Let's break down the solution step by step.
Step 1: Understand the given parameters
We have:
- Radius of the sphere, R=√3π m
- Surface charge density of the first hemisphere, σ1=√ϵ0×102 cm/m²
- Surface charge density of the second hemisphere, σ2=4σ1
Step 2: Convert units
Convert σ1 from cm/m² to m²:
σ1=√ϵ0×102 cm/m2=√ϵ0×102×10−4 m/m2=√ϵ0×10−2 m/m2
Step 3: Calculate the area of one hemisphere
The area A of a hemisphere is given by:
A=2πR2
Substituting R=√3π:
A=2π(√3π)2=2π⋅3π=6 m2
Step 4: Calculate the force of interaction
The force F0 between the two hemispheres can be calculated using the formula:
F0=12⋅Aϵ0⋅σ1⋅σ2
Substituting σ2=4σ1:
F0=12⋅6ϵ0⋅σ1⋅(4σ1)=12⋅6ϵ0⋅4σ21
F0=12σ212ϵ0=6σ21ϵ0
Step 5: Substitute σ1 into the force equation
Substituting σ1=√ϵ0×10−2:
F0=6(√ϵ0×10−2)2ϵ0=6⋅ϵ0⋅10−4ϵ0=6⋅10−4 N
Step 6: Express the force in terms of α
Given that F0=α×104 N:
6⋅10−4=α×104
To find α:
α=6
Conclusion
Thus, the value of α is 6.
We have:
- Radius of the sphere, R=√3π m
- Surface charge density of the first hemisphere, σ1=√ϵ0×102 cm/m²
- Surface charge density of the second hemisphere, σ2=4σ1
Convert σ1 from cm/m² to m²:
σ1=√ϵ0×102 cm/m2=√ϵ0×102×10−4 m/m2=√ϵ0×10−2 m/m2
The area A of a hemisphere is given by:
A=2πR2
Substituting R=√3π:
A=2π(√3π)2=2π⋅3π=6 m2
The force F0 between the two hemispheres can be calculated using the formula:
F0=12⋅Aϵ0⋅σ1⋅σ2
Substituting σ2=4σ1:
F0=12⋅6ϵ0⋅σ1⋅(4σ1)=12⋅6ϵ0⋅4σ21
F0=12σ212ϵ0=6σ21ϵ0
Substituting σ1=√ϵ0×10−2:
F0=6(√ϵ0×10−2)2ϵ0=6⋅ϵ0⋅10−4ϵ0=6⋅10−4 N
Given that F0=α×104 N:
6⋅10−4=α×104
To find α:
α=6
Thus, the value of α is 6.
Topper's Solved these Questions
Similar Questions
Two parallel large thin metal sheets have equal surface charge densities (σ=26.4×10−12C/m2) of opposite signs. The electric field between these sheets is
View SolutionA thin spherical shell of radius R is cut into two equal halves and then each of its halves is charged to the same uniform surface charge density σ. If F is the force exerted on each half to keep them at equilibrium, then F is proportional to
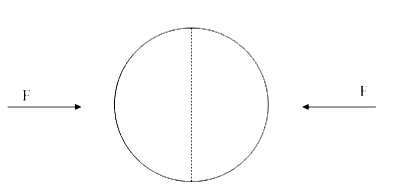 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
When a charge of amount Q is given to an isolated metal plate X of surface area A, its surface charge density becomes σ1. When an isolated identical plate Y is brought close to X the surface charge density on X becomes σ2. When Y is earthed the surface charge density on X becomes σ3. Choose the incorrect option.
Aσ1=QABσ1=Q2ACσ1=σ2Dσ3=QA
Two uniformly charged non-conducting hemispherical shells each having uniform charge density σ and radius R from a complete sphere (not stuck together) and surround a concentric spherical conducting shell of radius R/2. If hemispherical parts are in equilibrium then minimum surface charge density of inner conducting shell is :
View SolutionThe surface charge density of a thin charged disc of radius R is σ. The value of the electric field at the centre of the disc σ2∈0. With respect to the field at the centre, the electric field along the axis at a distance R from the centre of the disc is
View SolutionTwo spherical conductors of radii 4cmand5cm are charged to the same potential. If σ1andσ2 be respective value of surface density of charge on both the conductors, then the ratio of σ1/σ2 will be
View SolutionFigure shown two infinitely large conducting plates A and B. If electric field at C due to charge densities σ1,σ2,σ3 and σ40 is Eˆi, find σ2 and σ3 in terms of E. Derive a relation between σ1 and σ4.
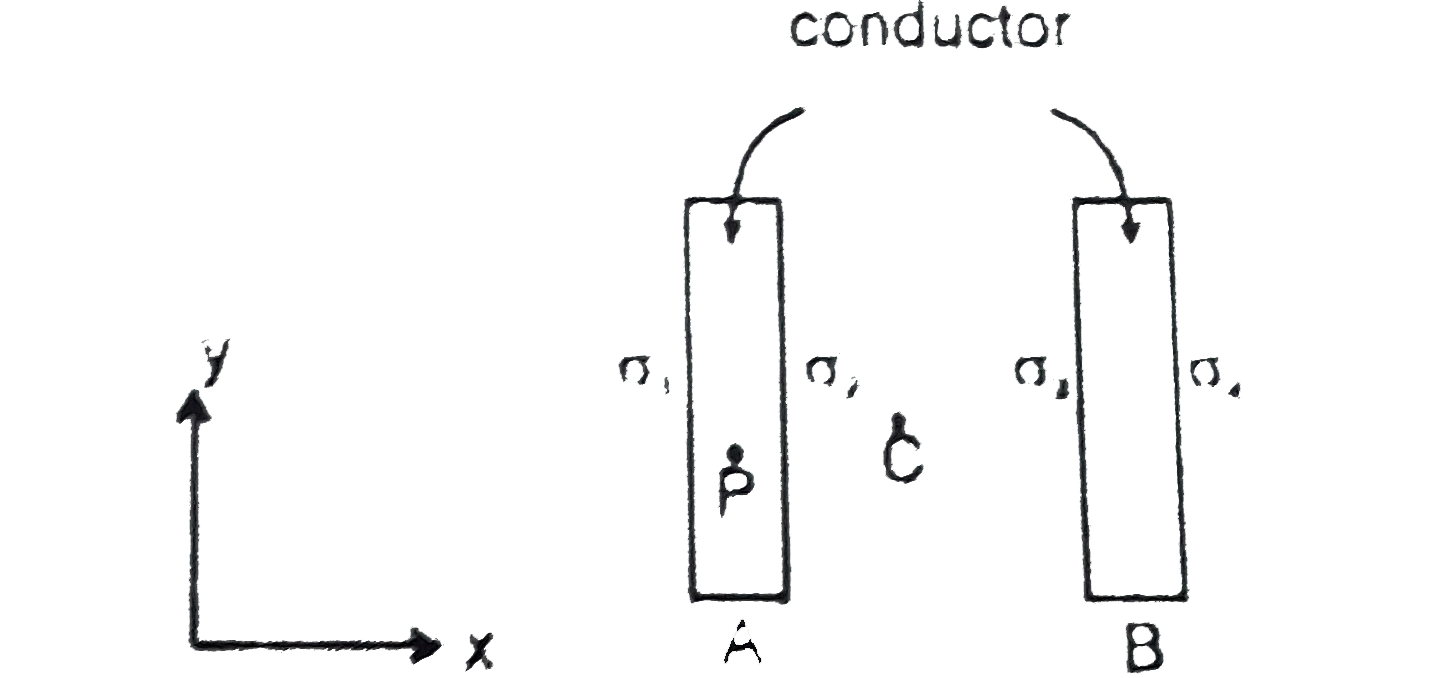 View Solution
View SolutionA large sheet carries uniform surface charge density σ . A rod of length 2l has a linear charge density λ on one half and −λ on the second half. The rod is hinged at the midpoint O and makes an angle θ with the normal to the sheet. The torque experience by the rod is
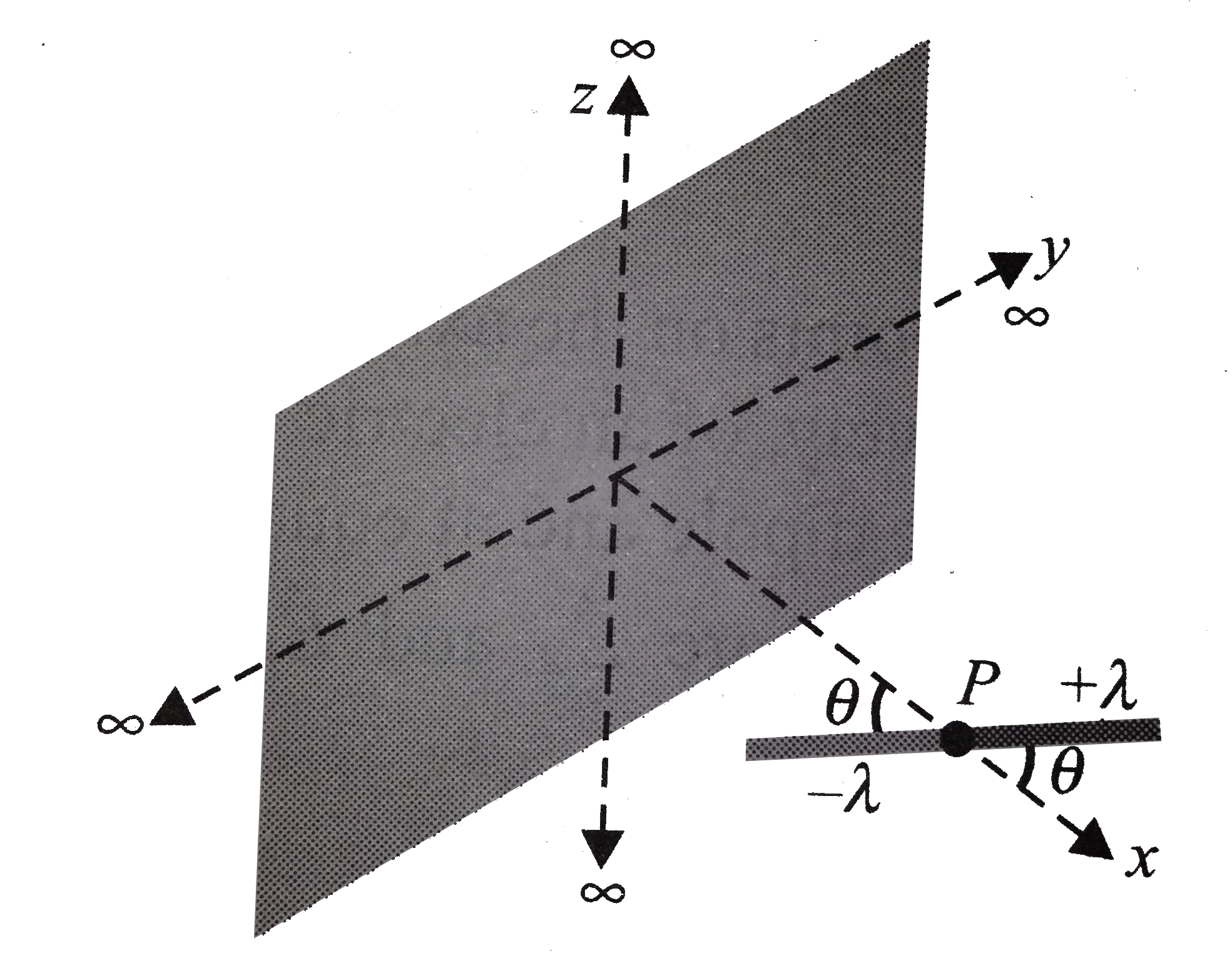 View Solution
View SolutionA total charge of 5μC is distributed uniformly on the surface of the thin walled semispherical cup. If the electric field strength at the centre of the hemisphere is 9×108NC−1, then the radius of the cup is
(14πε0=9×109N−m2C−2)View SolutionA slab of a material of dielectric constaant 2 is placed between two identical parallel plates. One of the plates carries total charge density +2mC/m2 and the other plate carries total charge density -4mC/m2 the magnitude of electric field inside the dielectric in (in 1011N/C) Take ε0=809×10−12Nm2/C2)
View Solution

