A point mass is subjected to two simultaneous sinusoidal displacement in x-direction, x1(t)=Asinωt and x2(t)=Asin(ωt+2π/3). Adding a third sinusoidal displacement x3(t)=Bsin(ωt+ϕ) brings the mass to a complete rest. The values of B and ϕ are :
√2A,3π4
A,4π3
√3A,5π6
A,π3
The correct Answer is:B
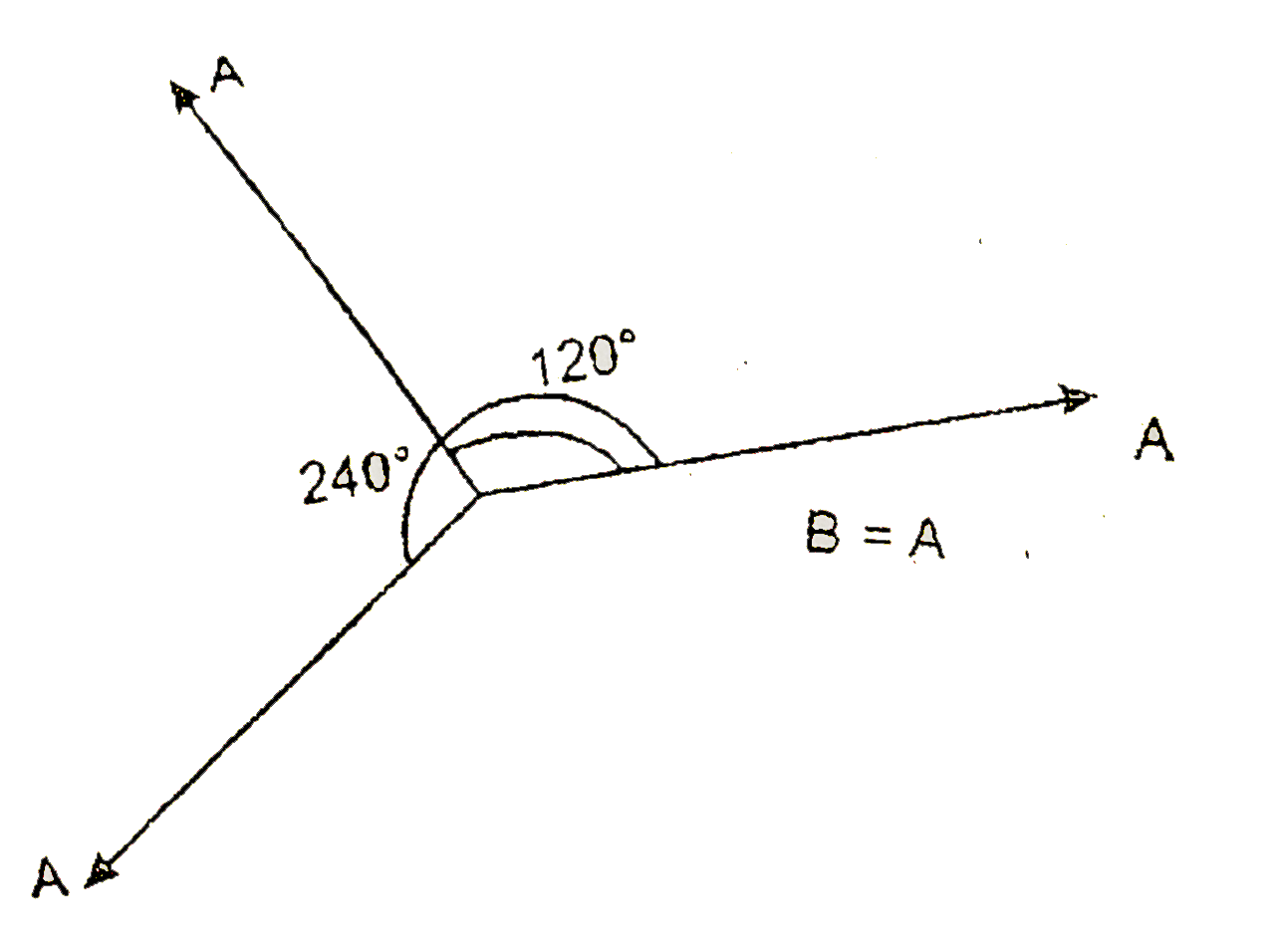
So B=A,ϕ=240∘=4π3
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Exercise- 3, PART - II17videos
SIMPLE HARMONIC MOTION
- BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Advanced Level Problems13videos
SIMPLE HARMONIC MOTION
- BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Exercise- 2, PART - IV8videos
SIMPLE HARMONIC MOTION
- BOOK - RESONANCE ENGLISHCHAPTER - SEMICONDUCTORSEXERCISE - Exercise 388videos
SEMICONDUCTORS
- BOOK - RESONANCE ENGLISHCHAPTER - TEST PAPERSEXERCISE - PHYSICS784videos
TEST PAPERS
Similar Questions
A point mass is subjected to two simultaneous sinusoidal displacements in x−direction,x1(t)=Asin(ω)tandx2(t)=Asin((ωt+2π3). Adding a third sinusoidal displacement x3(t)=Bsin(ωt+ϕ) brings the mas to a complete rest. The values of (B) and (phi) are.
View SolutionA partical is subjucted to two simple harmonic motions
x1=A1sinωt
and x2=A2sin(ωt+π/3)
Find(a) the displacement att=0, (b) the maximum speed of the partical and ( c) the maximum acceleration of the partical.View Solutionx and y displacements of a particle are given as x(t)=−asinωt and y(t)=asin2ωt. Its trajectory will look like.
View SolutionA particle is subjected to two simple harmonic motions
x1=A1sinωt
andx2=A2sin(ωt+π3)
Find a the displacement at t=0, b. the maxmum speed of the particle and c. the maximum acceleration of the particleView SolutionWhat is the phase difference between two simple harmonic motions represented by x1=Asin(ωt+π6) and x2=Acosωt?
View SolutionA particle is subjected to two simple harmonic motions.
x1=4.0sin(100πt) and x2=3.0sin(100πt+π3)
Find
(a) the displacement at t=0
(b) the maximum speed of the particle and
(c ) the maximum acceleration of the particle.View SolutionA xandy co-ordinates of a particle are x=Asin(ωt)andy=Asin(ωt+π/2). Then, the motion of the particle is
 View Solution
View SolutionFind the displacement equation of the simple harmonic motion obtained by combining the motion.
x1=2sinωt, x2=4sin(ωt+π6) and x3=6sin(ωt+π3)View SolutionA particle is subjected to two simple harmonic motions given by
x1=2.0sin(100πt) and x2=2.0sin(120πt+π/3)
where, x is in cm and t in second. Find the displacement of the particle at
(a) t=0.0125,
(b) t=0.025.View SolutionFind the displacement equation of the simple harmonic motion obtained by conbining the motions.
x1=2sin ωt,x2=4sin (ωt+π6)
and x3=6sin(ωt+π3)View Solution
