Two independent harmonic oscillators of equal mass are oscillating about the origin with angular frequencies ω1 and ω2 and have total energies E1 and E2 respectively. The variations of their momenta p with positions x are shown in figures. If ab=n2 and aR=n then the correct equation(s) is (are):
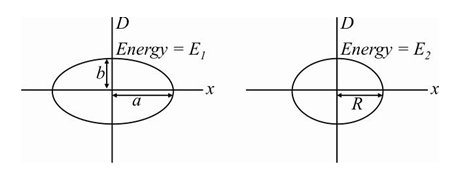
E1ω1=E2ω2
ω2ω1=n2
ω1ω2=n2
E1ω1=E2ω2
The correct Answer is:B, D
For first oscillarator , For second oscillator
b=maω1
ab=1mω1=n2,1mω2=1
ω2ω1=n2
E1=12mω21a2,E3=12mω22R2
E1E2=ω21ω22×n2=ω21ω22×ω2ω1,E1E2=ω1ω2⇒E1ω1=E2ω2
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Exercise- 3, PART - II17videos
SIMPLE HARMONIC MOTION
- BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Advanced Level Problems13videos
SIMPLE HARMONIC MOTION
- BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Exercise- 2, PART - IV8videos
SIMPLE HARMONIC MOTION
- BOOK - RESONANCE ENGLISHCHAPTER - SEMICONDUCTORSEXERCISE - Exercise 388videos
SEMICONDUCTORS
- BOOK - RESONANCE ENGLISHCHAPTER - TEST PAPERSEXERCISE - PHYSICS784videos
TEST PAPERS
Similar Questions
Two independent harmonic oscillators of equal mass are oscillating about the origin with angular frequencies ω1 and ω2 and have total energies E1 and E2 repsectively. The variations of their momenta p with positions x are shown in figures. If ab=n2 and aR=n, then the correc t equation(s) is (are) :
 View Solution
View SolutionTwo bodies of different masses m1 and m2 have equal momenta. Their kinetic energies E1 and E2 are in the ratio
View SolutionTwo bodies of different masses m1 and m2 have equal momenta. Their kinetic energies E1 and E2 are in the ratio
View SolutionTwo bodies of different masses m1 and m2 have equal momenta. Their kinetic energies E1 and E2 are in the ratio
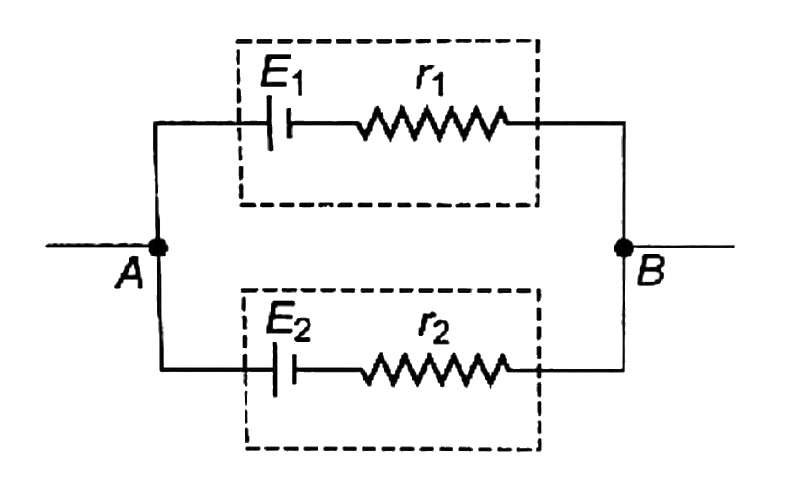
View SolutionTwo batteries of emf E1andE2(E2>E1) and internal resistances r1andr2 respectively are connected in parallel as shown in figure.
 View Solution
View SolutionTwo discs A and B are in contact and rotating with angular velocity with angular velocities ω1andω2 respectively as shown. If there is no slipping between the discs, then
 View Solution
View SolutionIn forced oscillation of a particle the amplitude is maximum for a frequency ω1 of the force while the energy is maximum for a frequency ω2 of the force, then .
View SolutionTwo batteries of emf E1 and E2(E2>E1) and internal resistance r1 and r2 respectively are connected in parallel as shown in the figure. Then, which of the followings statements is correct ?
 View Solution
View SolutionTwo bodies with masses m1kgandm2kg have equal kinetic energies. If p1andP2 are their respective momenta, then p1/P2 is equal to :
View SolutionA particle performing SHM with angular frequency ω=5000 radian/second and amplitude A=2 cm and mass of 1 kg. Find the total energy of oscillation.
View Solution
