A uniform thin cylindrical disc of mass M and radius R is attached to two identical massless springs of spring constant k which are fixed to the wall as shown in Fig. The springs are attached to the axle of the disk symmetrically on either side at a distance d from its centre. The axle is massless and both the springs and the axle are in horizontal plane. The unstretched length of each spring is L. The disc is initially at its equilibrium position with its centre of mass (CM) at a distance L from the wall. The disc rolls without slipping with velocity V0=V0ˆi. The coefficient of friction is μ
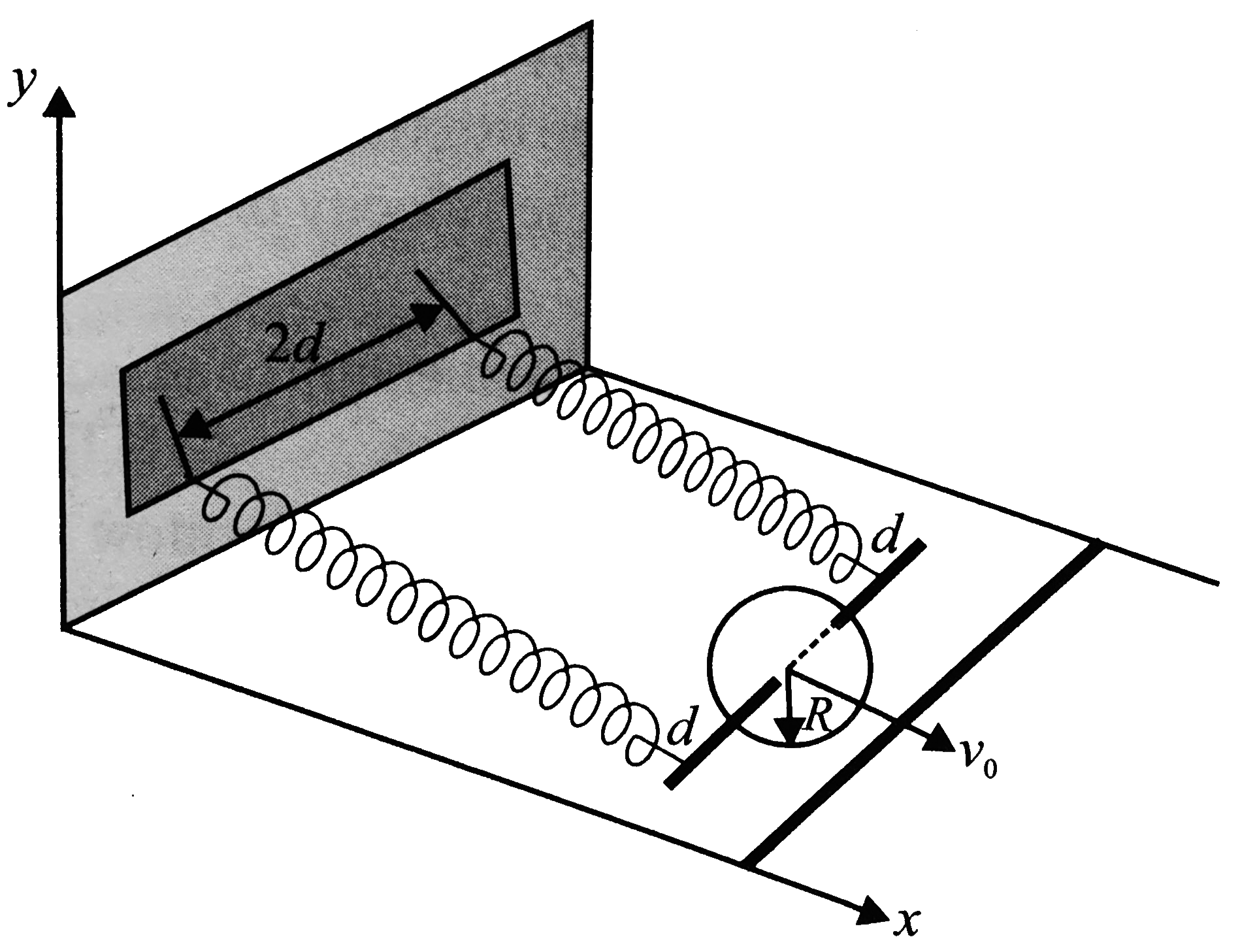
The maximum value of V0 for which the disc will roll without slipping is
μg√Mk
μg√M2k
μg√3Mk
μg√5M2k
The correct Answer is:C
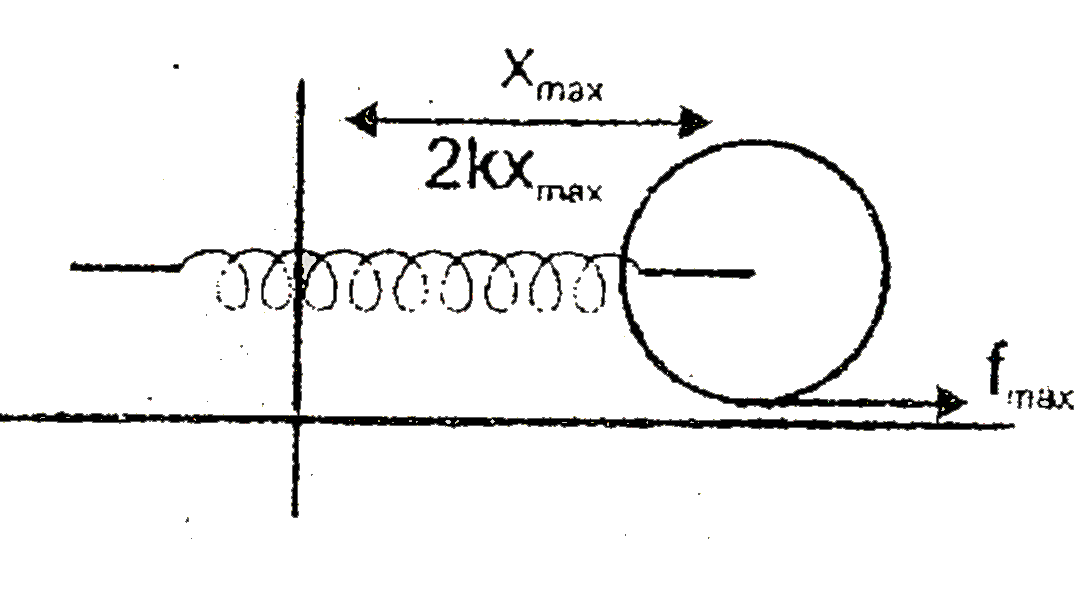
12MV02+12MR22(V0R)2=12(2K)x2max
=32MV02=2kx2max⇒xmax=√34Mv02K
At extreme position, frication will have maximum value.
2kxmx−fmax=4k3xmax⇒fmax=23kxmx
μMg=23=23k√34Mv02K⇒μMg=(√K3M)V0
V0=μMG√3MK
Topper's Solved these Questions
- SIMPLE HARMONIC MOTION BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Exercise- 3, PART - II
17 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Advanced Level Problems
13 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Exercise- 2, PART - IV
8 Videos
- SEMICONDUCTORSBOOK - RESONANCE ENGLISHCHAPTER - SEMICONDUCTORSEXERCISE - Exercise 3
88 Videos
- TEST PAPERSBOOK - RESONANCE ENGLISHCHAPTER - TEST PAPERSEXERCISE - PHYSICS
784 Videos
Similar Questions
A uniform thin cylindrical disk of mass M and radius R is attaached to two identical massless springs of spring constatn k which are fixed to the wall as shown in the figure. The springs are attached to the axle of the disk symmetrically on either side at a distance d from its centre. The axle is massless and both the springs and the axle are in horizontal plane. the unstretched length of each spring is L. The disk is initially at its equilibrium position with its centre of mass (CM) at a distance L from the wall. The disk rolls without slipping with velocity →V0=vacV0ˆi. The coefficinet of friction is μ.

The maximum value of V0 for whic the disk will roll without slipping is-
View SolutionA uniform thin cylindrical disk of mass M and radius R is attaached to two identical massless springs of spring constatn k which are fixed to the wall as shown in the figure. The springs are attached to the axle of the disk symmetrically on either side at a distance d from its centre. The axle is massless and both the springs and the axle are in horizontal plane. the unstretched length of each spring is L. The disk is initially at its equilibrium position with its centre of mass (CM) at a distance L from the wall. The disk rolls without slipping with velocity →V0=vacV0ˆi. The coefficinet of friction is μ.
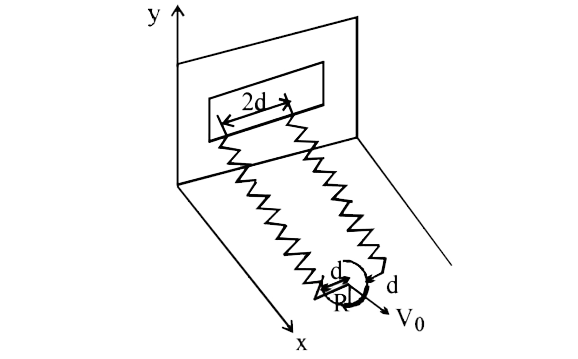
The centre of mass of the disk undergoes simple harmonic motion with angular frequency ω equal to -
View SolutionA uniform thin cylindrical disk of mass M and radius R is attaached to two identical massless springs of spring constatn k which are fixed to the wall as shown in the figure. The springs are attached to the axle of the disk symmetrically on either side at a distance d from its centre. The axle is massless and both the springs and the axle are in horizontal plane. the unstretched length of each spring is L. The disk is initially at its equilibrium position with its centre of mass (CM) at a distance L from the wall. The disk rolls without slipping with velocity →V0=vacV0ˆi. The coefficinet of friction is μ.
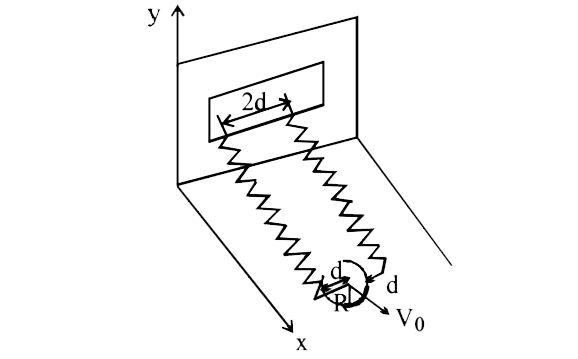
The net external force acting on the disk when its centre of mass is at displacement x with respect to its equilibrium position is.
View SolutionTwo identical massless springs A and B consist spring constant kA and kB respectively. Then :
View SolutionA block of mass m is connected to another .block of mass M by a massless spring of spring constant k. A constant force f starts action as shown in figure, then:

View SolutionA small ball of mass M=1 kg is attached to two identical springs of constant 100N/m, which are attached to floor and roof. The springs are initially unstretched. By what distance ball comes down to attain equilibrium? (in cm)

View SolutionTwo identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in the figure. The time period of oscillation is

View SolutionAn object of mass 'm' is attached to a vertical fixed spring of spring constant 'k' and is allowed to fall under the gravity. What is the distance traversed by the object before being stopped ?
View SolutionTwo equal masses are attached to the two ends of a spring of spring constant k. The masses are pulled out symmetrically to stretch the spring by a length x over its natural length. The work done by the spring one each mass is
View SolutionA block of mass m is kept on a rough horizontal surface and is attached with a massless spring of force constant k. The minimum constant force applied on the other end of the spring of lift the block is
View Solution
