A conducting square loop of side l and resistance R moves in its plane with a uniform velocity v perpendicular ot one of its sides. A uniform and constant magnetic field B exists along the perpendicualr ot the plane of the loop as shown in . The current induced in the loop is
(##HCV_VOL2_C38_E01_025_Q01##)
BlvRclockwise
BlvR anti-clockwise
2BlvR anti-clockwise
zero
The correct Answer is:A
To solve the problem of the induced current in a conducting square loop moving in a magnetic field, we can follow these steps:
Step 1: Understand the setup
We have a square loop of side length l and resistance R. The loop is moving with a uniform velocity v perpendicular to one of its sides. There is a uniform magnetic field B that is perpendicular to the plane of the loop.
Step 2: Determine the area of the loop
The area A of the square loop is given by:
A=l2
Step 3: Analyze the magnetic flux
The magnetic flux Φ through the loop is given by the product of the magnetic field B and the area A:
Φ=B⋅A=B⋅l2
Step 4: Check for change in magnetic flux
Since the loop is moving with a constant velocity v and the magnetic field B is uniform and constant, the area of the loop that is within the magnetic field does not change. Therefore, the magnetic flux Φ remains constant over time.
Step 5: Apply Faraday's law of electromagnetic induction
According to Faraday's law, the induced electromotive force (EMF) E in the loop is given by the negative rate of change of magnetic flux:
E=−dΦdt
Since Φ is constant, we have:
dΦdt=0
Thus, the induced EMF E is:
E=0
Step 6: Determine the induced current
Using Ohm's law, the induced current I in the loop can be calculated as:
I=ER
Since E=0, we find:
I=0R=0
Conclusion
The current induced in the loop is zero.
We have a square loop of side length l and resistance R. The loop is moving with a uniform velocity v perpendicular to one of its sides. There is a uniform magnetic field B that is perpendicular to the plane of the loop.
The area A of the square loop is given by:
A=l2
The magnetic flux Φ through the loop is given by the product of the magnetic field B and the area A:
Φ=B⋅A=B⋅l2
Since the loop is moving with a constant velocity v and the magnetic field B is uniform and constant, the area of the loop that is within the magnetic field does not change. Therefore, the magnetic flux Φ remains constant over time.
According to Faraday's law, the induced electromotive force (EMF) E in the loop is given by the negative rate of change of magnetic flux:
E=−dΦdt
Since Φ is constant, we have:
dΦdt=0
Thus, the induced EMF E is:
E=0
Using Ohm's law, the induced current I in the loop can be calculated as:
I=ER
Since E=0, we find:
I=0R=0
The current induced in the loop is zero.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrance special format questions17videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Match the columns5videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Check point60videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery97videos
CURRENT ELECTRICITY
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C22videos
ELECTROMAGNETIC WAVES
Similar Questions
A semicircular loop of radius R is rotated with an angular velocity ω perpendicular to the plane of a magnetic field B as shown in the figure. Emf Induced in the loop is
 View Solution
View SolutionA circular loop of radius R is kept in a uniform magnetic field pointing perpendicular into the plane of paper. When a current l flows in the loop, the tension produced in the loop is
 View Solution
View SolutionA conducting loop confined in a plane is rotated in its own plane with some angular velocity.A uniform and constant magnetic field exist in the region.Find the current induced in the loop.
View SolutionA loop PQR carries a current i=2A as shown in the figure. A uniform magnetic field B = 2T exists in space parallel to the plane of the loop . The magnetic torque on the loop is
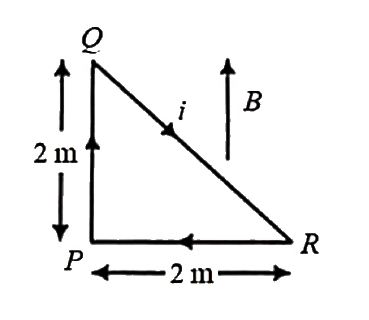 View Solution
View SolutionA triangular loop of side l carries a current I. It is placed in a magnetic field B such that the plane of the loop is in the direction of B. The torque on the loop is
View SolutionA triangular loop of side l carries a current l. It is placed in a magnetic field B such that the plane of the loop is in the direction of B. The torque on the loop is
View SolutionA right angled triangle abc, made from a metallic wire, moves at a uniform speed v in its plane as shown in . A uniform magnetic field B exists in the perpendicular direction. Find the emf induced (a) in the loop abc, (b) in the segment bc, (c ) in the segment ac and (d) in the segment ab.
(##HCV_VOL2_C38_E01_066_Q01##)View SolutionA square loop of side 10 cm and resistance 1 Omega is moved towards right with a constant velocity V_0 as shown in . The left arm of the loop is in a uniform magnetic field of 2 T. the field is perpendicular ot the plane of the drawing and is going into it. the loop is connected to a network of resistors each of value 3 Omega with what speed should the loop be moved so that a steady curfrent of 1 mA flows in the loop.
 View Solution
View SolutionA uniform circular loop of radius a and resistance R palced perpendicular to a uniform magnetic field B. One half of the loop is rotated about the diameter with angular velocity ω as shown in Fig. Then, the current in the loop is
 View Solution
View SolutionA uniform circular loop of radius a and resistance R palced perpendicular to a uniform magnetic field B. One half of the loop is rotated about the diameter with angular velocity ω as shown in Fig. Then, the current in the loop is
 View Solution
View Solution

