In an alternating circuit applied voltage is 200V, if R=8WXL=XC=6Ω then write the value of the following
(a)Root mean square value of voltage
(b)Impedance of circuit.
To solve the problem step by step, we will calculate the root mean square (RMS) voltage and the impedance of the circuit.
Given Data:
- Applied Voltage (V_p) = 200 V
- Resistance (R) = 8 Ω
- Inductive Reactance (X_L) = 6 Ω
- Capacitive Reactance (X_C) = 6 Ω
Step 1: Calculate the Root Mean Square (RMS) Voltage
The formula for the root mean square voltage (V_rms) is given by:
Vrms=Vp√2
Substituting the given values:
Vrms=200V√2≈2001.414≈141.42V
Step 2: Calculate the Impedance of the Circuit
The impedance (Z) of an RLC circuit is calculated using the formula:
Z=√R2+(XL−XC)2
Since XL and XC are both equal to 6 Ω, we can simplify the equation:
Z=√R2+(XL−XC)2=√R2+(6−6)2=√R2+0
Thus, we have:
Z=√R2=R
Substituting the value of R:
Z=√82=8Ω
Final Answers:
(a) The root mean square value of the voltage Vrms≈141.42V
(b) The impedance of the circuit Z=8Ω
---
- Applied Voltage (V_p) = 200 V
- Resistance (R) = 8 Ω
- Inductive Reactance (X_L) = 6 Ω
- Capacitive Reactance (X_C) = 6 Ω
The formula for the root mean square voltage (V_rms) is given by:
Vrms=Vp√2
Substituting the given values:
Vrms=200V√2≈2001.414≈141.42V
The impedance (Z) of an RLC circuit is calculated using the formula:
Z=√R2+(XL−XC)2
Since XL and XC are both equal to 6 Ω, we can simplify the equation:
Z=√R2+(XL−XC)2=√R2+(6−6)2=√R2+0
Thus, we have:
Z=√R2=R
Substituting the value of R:
Z=√82=8Ω
(a) The root mean square value of the voltage Vrms≈141.42V
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - A.L.P10videos
ALTERNATING CURRENT
- BOOK - RESONANCE ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - EXAMPLE40videos
ALTERNATING CURRENT
- BOOK - RESONANCE ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Exercise -3 Part-23videos
ALTERNATING CURRENT
- BOOK - RESONANCE ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - Advanved level problems17videos
ATOMIC PHYSICS
Similar Questions
An alternating voltage is given by: e=e1sinωt+e2cosωt. Then the root mean square value of voltage is given by:
View SolutionAn alternating voltage is given by: e=e1sinωt+e2cosωt. Then the root mean square value of voltage is given by:
View SolutionIn a series L−C circuit, the applied voltage is V0. if omega is very low, then the voltage drop across the inductor VL and capacitor VC are
 .View Solution
.View SolutionIn an L-C-R series circuit R = 10Ω,XL=8Ωand XC=6Ωthe total impedance of the circuit is -
View SolutionIn an LCR series ac circuit the voltage across L,C and R are V1,V2 and V3 respectively The voltage of the source is .
View SolutionIn a series L−C−R circuit, currenrt in the circuit is 11A when the applied voltage is 220V. voltage across the caspcitor is 200V. If the value of resistor is 20Ω, then the voltage across the unknown inductor is
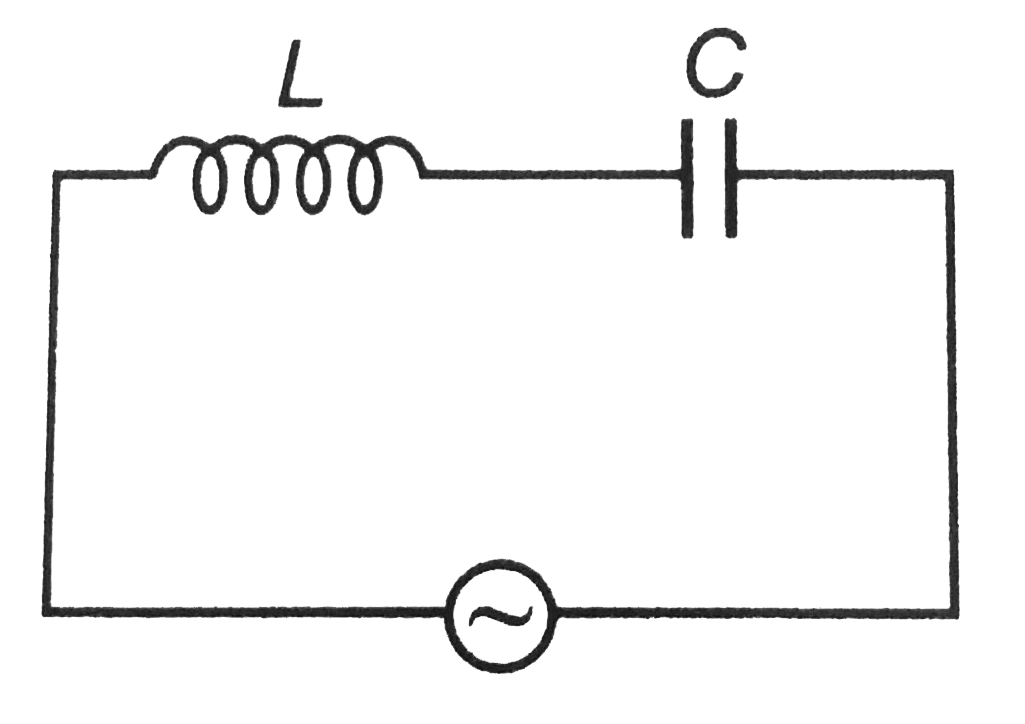
View SolutionIn an AC, series L-C-R circuit, R=XL=XC and applied AC, voltage is V. Then match the following two columns.
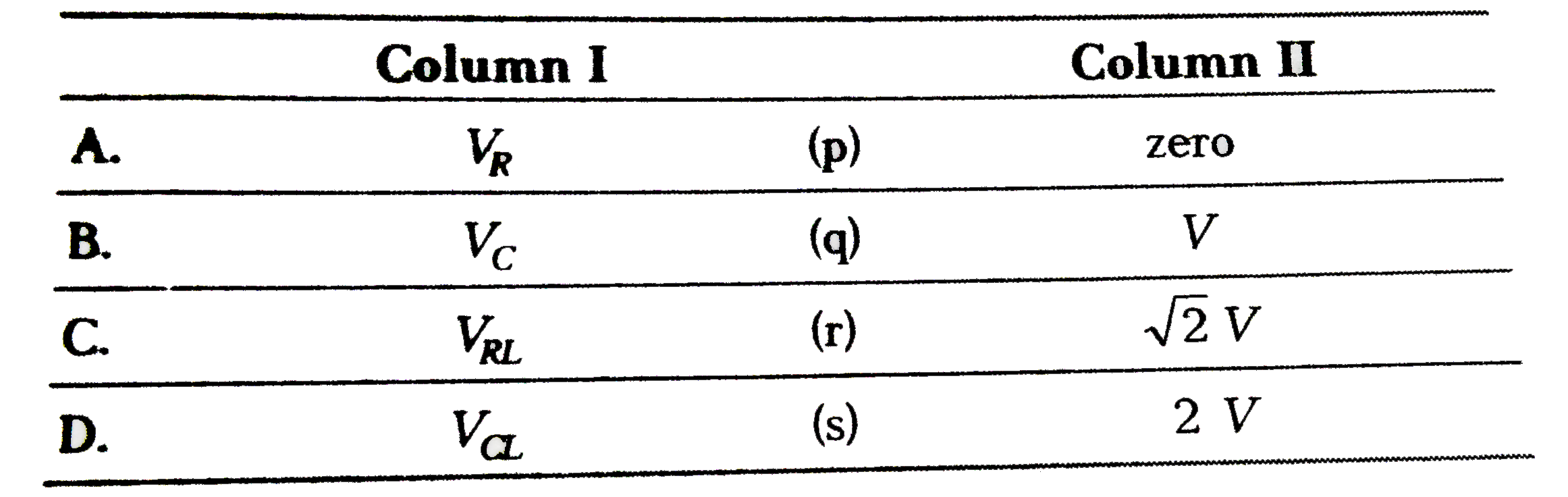 View Solution
View SolutionThe equation of an alternating voltage is E=220sin(ωt+π/6) and the equation of the current in the circuit is I=10sin(ωt−π/6). Then the impedance of the circuit is
View SolutionIn an AC series L−C−R circuit, applied voltage is
V=(100√2sin(ωt+45∘))V
Given that, R=30Ω, XL=50Ω and XC=10Ω Now match the following two columns.
 View Solution
View SolutionIn series LCR circuit, the voltages across R, L and C are shown in the figure. The voltage of applied source
 View Solution
View Solution

