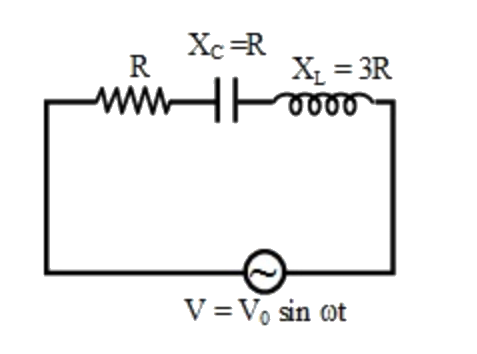A voltage V=V0sinωt is applied to a series LCR circuit. Derive expression for the average power dissipated over a cycle.
Under What condition (i) no power is dissipated even though the current flows through the circuit?
(ii) Maximum power is dissipated in the circuit?
Video Solution
Text Solution
Current in this circuit will be I=I0sin(wt+ϕ)
where
ϕ=tan−1(xL−xCxR)
xL=wL,x=1WC,xR=R
P∈st=V.I
=(v0sinwt)[l0sin(wt+ϕ)]
=v0I0(sinwt)[sin(wt+ϕ)]
=v0I022sinwt[sin(wt+ϕ)]
v0I02[cos−(wt−(wt+ϕ)−cos(2wt+ϕ)]
Pavg=ITT∫0P∈stdt
=ITT∫0v0I02[(cosϕ)−cos(2wt+ϕ)]dt
T=2πω,wt=θ
wdt=dthη
12π2π∫0v0I02[(cosϕ)−cos(2wt+ϕ)]dθ
⇒v0I02cosϕ−O
v0I02cosϕ⇒vrms−Irmscosϕ
(i)no power is dissipated if ϕ=π2 i.e. R=0.
(ii)Maximum power is dissipated if ϕ=0 i.e. w2=1LC
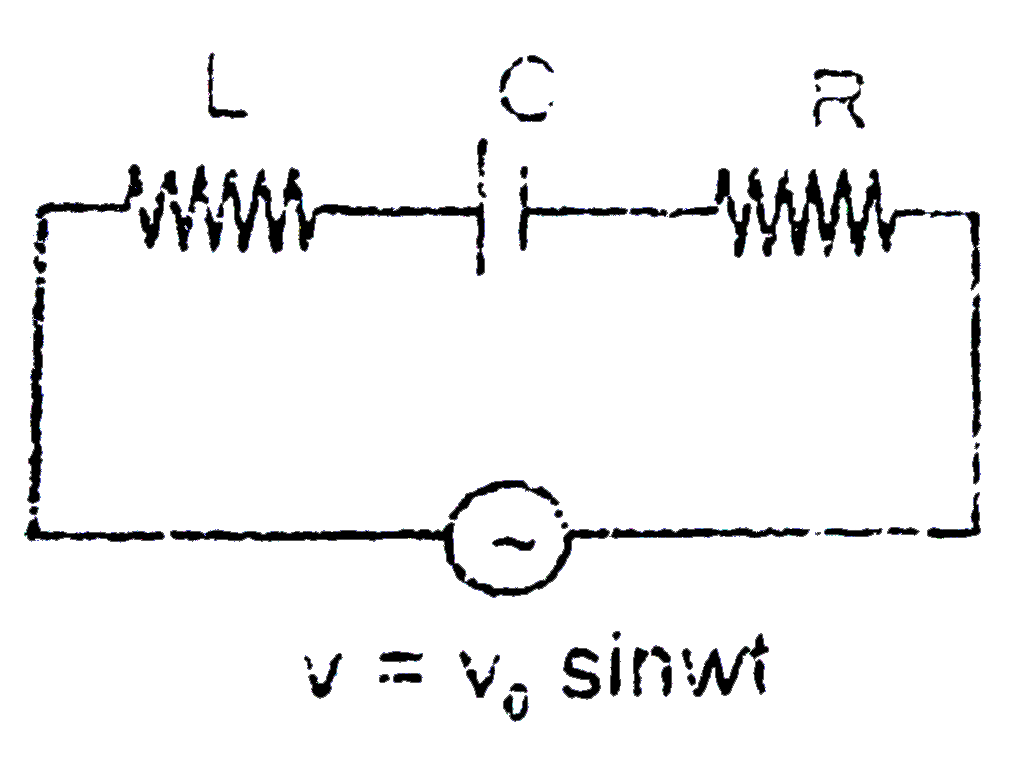
|
Topper's Solved these Questions
- ALTERNATING CURRENTBOOK - RESONANCE ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - A.L.P
10 Videos
- ALTERNATING CURRENTBOOK - RESONANCE ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - EXAMPLE
40 Videos
- ALTERNATING CURRENTBOOK - RESONANCE ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Exercise -3 Part-2
3 Videos
- ATOMIC PHYSICSBOOK - RESONANCE ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - Advanved level problems
17 Videos
Similar Questions
Knowledge Check
In which of following circuits the maximum power dissipation is observed?
APure capacitive circuitBPure inductive circuitCPure resistive circuitDNone of theseA current of 3A flows through the 2Ω resistor as shown in the circuit. The power dissipated in the 5Ω resistor is
 A5 watt.B4 watt.C2 watt.D1 watt
A5 watt.B4 watt.C2 watt.D1 watt
The average power dissipation in a pure capacitance in AC circuit is
View SolutionIn a LCR series resonating circuit. Give the value of average power loss.
View SolutionIn an AC circuit with voltage V and current I, the power dissipated is
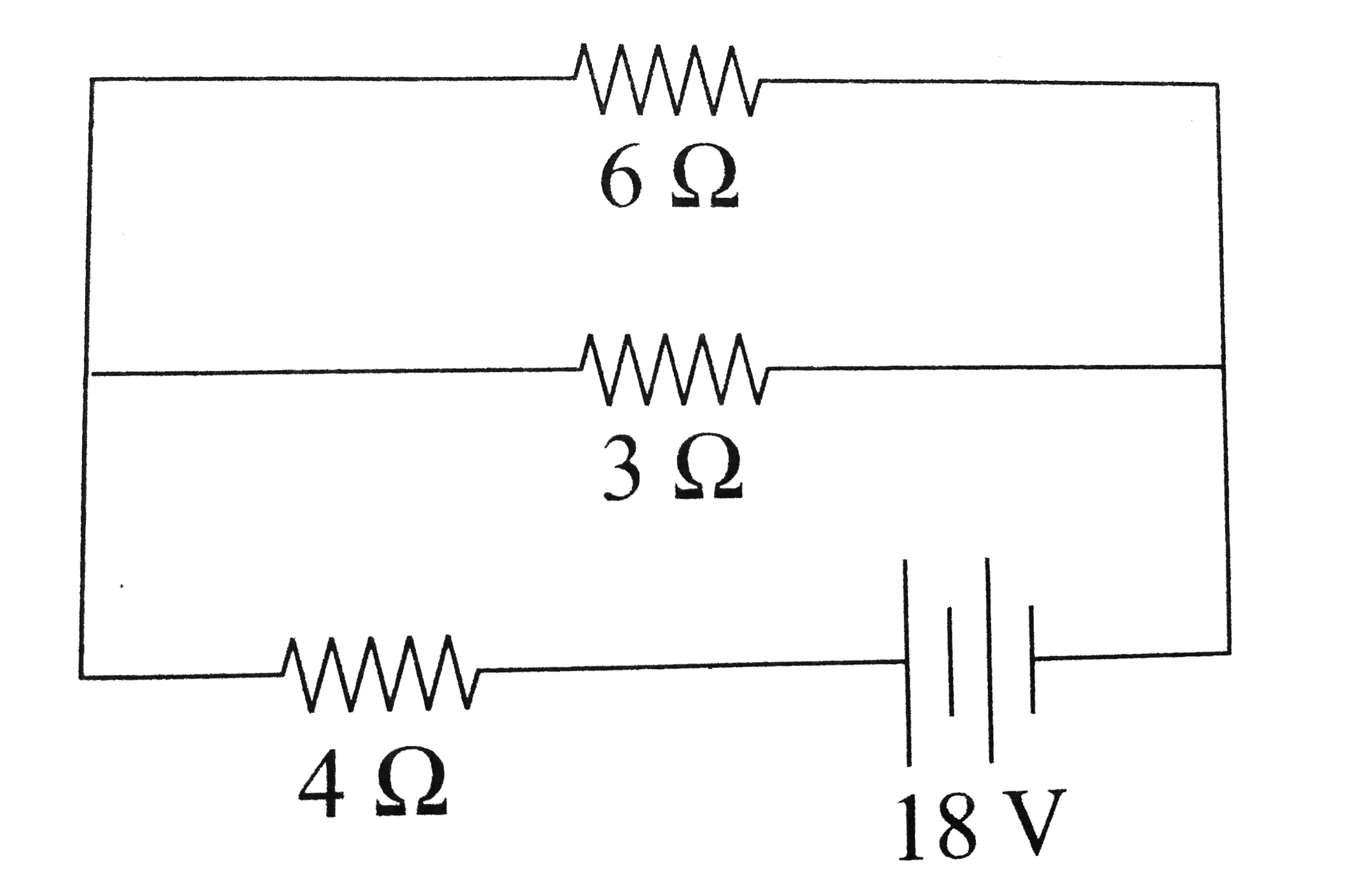
View SolutionThe total power dissipated in watts in the circuit shown here is
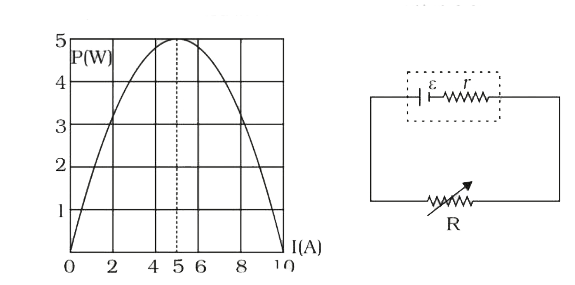
View SolutionFigure shows the net power dissipated in R versus the current in a simple circuit shown.
View SolutionIn the circuit shown, the average power dissipated in the resistor is (assume diode to be ideal)
View Solution