A block of a mass of 10 kg rests on a horizontal table. The coefficient of friction between the block and the table is 0.05. When hit by a bullet of mass 50 g moving with speed v, that gets embedded in it, the block moves and comes to rest after moving a distance of 2 m on the table. If a freely falling object were to acquire speed 10v after being dropped from height H, then neglecting energy losses and taking g=10 S.I. , the value of H is close to:
a) 0.05 km
b) 0.02 km
c) 0.03 km
d) 0.04 km
The correct Answer is:A
To solve the problem step by step, we will break it down into parts:
Step 1: Understand the Problem
We have a block of mass m=10kg resting on a table with a coefficient of friction μ=0.05. A bullet of mass mb=50g=0.05kg hits the block with speed v and embeds itself in the block. After the collision, the block moves a distance of s=2m before coming to rest.
Step 2: Apply Conservation of Momentum
Using the conservation of momentum for the bullet and the block:
mbv=(m+mb)v′
where v′ is the velocity of the block and bullet after the collision.
Substituting the values:
0.05v=(10+0.05)v′
0.05v=10.05v′
Thus, we can express v in terms of v′:
v=10.050.05v′=201v′
Step 3: Calculate the Frictional Force
The frictional force Ff acting on the block is given by:
Ff=μ(m+mb)g
Substituting the values:
Ff=0.05×(10+0.05)×10=0.05×10.05×10=5.025N
Step 4: Use Work-Energy Principle
The work done by the frictional force is equal to the kinetic energy lost by the block:
Ff⋅s=12(m+mb)v′2
Substituting the values:
5.025×2=12×10.05×v′2
10.05=5.025v′2
v′2=10.055.025=2
Thus,
v′=√2m/s≈1.414m/s
Step 5: Relate v and v′
From Step 2, we found:
v=201v′=201×1.414≈284.25m/s
Step 6: Calculate Height H
Now, we need to find the height H from which an object falls to acquire a speed of 10v:
10v=10×284.25=2842.5m/s
Using the equation of motion for free fall:
v2=2gH
Substituting v=2842.5m/s and g=10m/s2:
(2842.5)2=2×10×H
H=(2842.5)220
Calculating H:
H=8085006.2520=404250.3125m
Converting to kilometers:
H≈404.25km
Step 7: Compare with Options
Since the options are given in kilometers, we convert H to kilometers:
H≈0.404km
Thus, the closest option is 0.04km.
Final Answer
The value of H is close to 0.04km.
We have a block of mass m=10kg resting on a table with a coefficient of friction μ=0.05. A bullet of mass mb=50g=0.05kg hits the block with speed v and embeds itself in the block. After the collision, the block moves a distance of s=2m before coming to rest.
Using the conservation of momentum for the bullet and the block:
mbv=(m+mb)v′
where v′ is the velocity of the block and bullet after the collision.
0.05v=(10+0.05)v′
0.05v=10.05v′
Thus, we can express v in terms of v′:
v=10.050.05v′=201v′
The frictional force Ff acting on the block is given by:
Ff=μ(m+mb)g
Substituting the values:
Ff=0.05×(10+0.05)×10=0.05×10.05×10=5.025N
The work done by the frictional force is equal to the kinetic energy lost by the block:
Ff⋅s=12(m+mb)v′2
Substituting the values:
5.025×2=12×10.05×v′2
10.05=5.025v′2
v′2=10.055.025=2
Thus,
v′=√2m/s≈1.414m/s
From Step 2, we found:
v=201v′=201×1.414≈284.25m/s
Now, we need to find the height H from which an object falls to acquire a speed of 10v:
10v=10×284.25=2842.5m/s
Using the equation of motion for free fall:
v2=2gH
Substituting v=2842.5m/s and g=10m/s2:
(2842.5)2=2×10×H
H=(2842.5)220
Calculating H:
H=8085006.2520=404250.3125m
Converting to kilometers:
H≈404.25km
Since the options are given in kilometers, we convert H to kilometers:
H≈0.404km
Thus, the closest option is 0.04km.
The value of H is close to 0.04km.
Topper's Solved these Questions
- CAPACITANCEBOOK - RESONANCE ENGLISHCHAPTER - CAPACITANCEEXERCISE - Exercise - 3
26 Videos
- CAPACITANCEBOOK - RESONANCE ENGLISHCHAPTER - CAPACITANCEEXERCISE - High Level Problems
16 Videos
- CAPACITANCEBOOK - RESONANCE ENGLISHCHAPTER - CAPACITANCEEXERCISE - Exercise - 1
79 Videos
- ATOMIC PHYSICSBOOK - RESONANCE ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - Advanved level problems
17 Videos
- COMMUNICATION SYSTEMSBOOK - RESONANCE ENGLISHCHAPTER - COMMUNICATION SYSTEMSEXERCISE - Exercise 3
13 Videos
Similar Questions
A block of mass'm' is resting on the floor of a lift. The coefficient of friction between the block and the floor is μ. When the lift is falling freely, the limiting frictional force between block and surface is
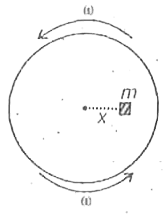
View SolutionA block of mass m is kept on horizontal turn table at x distance from the centre. If coefficient of friction between block and surface of turn table is μ, then maximum angular speed of the table so that block does not slip
View SolutionA bullet of mass 50 g moving with an initial velocity 100m s−1 strikes a wooden block and comes to rest after penetrating a distance 2 cm in it. Calculate : Final momentum of the bullet
View SolutionA block of mass m is kept on a horizontal table. If the static friction coefficient is μ., find the frictional force acting on the block.
View SolutionA block of mass m kept on rough horizontal turn table at a distance x from the centre. If the coefficient of friction between the table and block is μ then maximum speed of point P on turn table so that the block does not slip is

View SolutionA bullet of mass 50 g moving with an initial velocity 100m s−1 strikes a wooden block and comes to rest after penetrating a distance 2 cm in it. Calculate : Initial momentum of the bullet
View SolutionIf coeffiecient of friction between the block of mass 2kg and table is 0.4 then out acceleration of the system and tension in the string. (g=10m/s2)
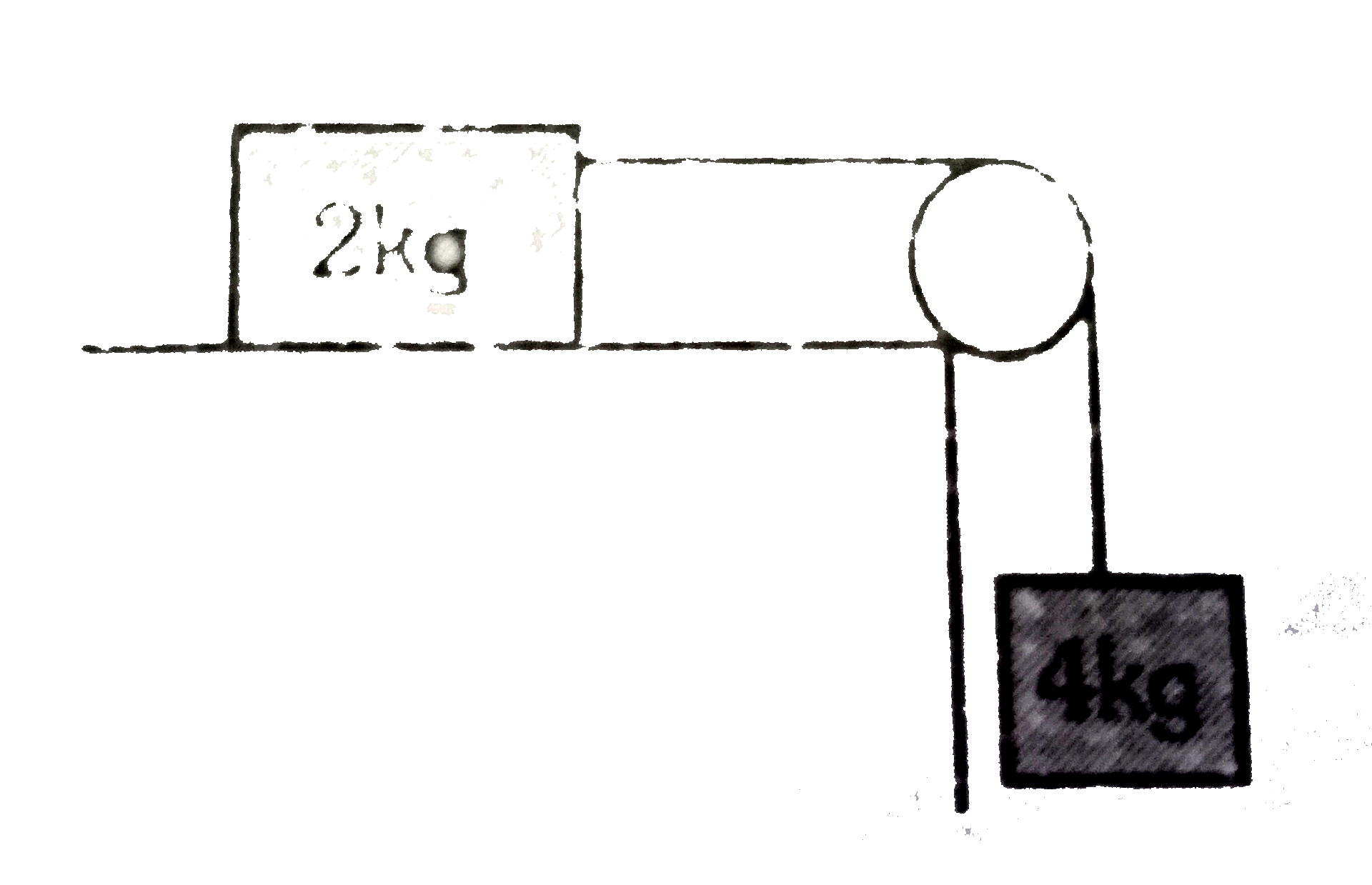
View SolutionA bullet of mass 50 g moving with an initial velocity 100m s−1 strikes a wooden block and comes to rest after penetrating a distance 2 cm in it. Calculate : Retardation caused by the wooden block
View SolutionA bullet of mass 10 g is fired horizontally into a 4 kg wooden block resting on a horizontal surface. The coefficient of kinetic friction between the block and the surface is 0.25. The bullet is embadded the block and the combination moves a distance of 20 m before coming to rest. Find the speed of the bullet just before striking the block. (g=10m/s2)
View SolutionA bullet of mass 50 g moving with an initial velocity 100m s−1 strikes a wooden block and comes to rest after penetrating a distance 2 cm in it. Calculate : Resistive force exerted by the wooden block.
View Solution
