An isolated metallic object is charged in vacuum to a potential V0 using a suitable source, its electrostatic energy being W0. It is then disconnected from the source and immersed in a large volume of dielectric with dielectric constant K. The electrostatic energy of the sphere in the dielectric is :
K2W0
KW0
W0K2
W0K
The correct Answer is:D
To solve the problem step by step, we will analyze the situation before and after the metallic object is immersed in the dielectric medium.
Step 1: Understand the Initial Conditions
Initially, the isolated metallic object is charged in vacuum to a potential V0. The electrostatic energy associated with this charge is given as W0.
Step 2: Relate Charge, Capacitance, and Energy
The charge q on the object can be expressed in terms of its capacitance C0 and potential V0:
q=C0⋅V0
The electrostatic energy W0 can be expressed as:
W0=12C0V20
Step 3: Insert the Object into Dielectric
When the metallic object is immersed in a dielectric medium with dielectric constant K, the capacitance of the object changes. The new capacitance C becomes:
C=K⋅C0
Since the charge q remains constant (as the object is isolated), we can express the new potential V in terms of the new capacitance:
V=qC=C0V0K⋅C0=V0K
Step 4: Calculate the New Electrostatic Energy
The new electrostatic energy W in the dielectric can be calculated using the new capacitance and potential:
W=12CV2
Substituting the expressions for C and V:
W=12(K⋅C0)(V0K)2
Simplifying this expression:
W=12KC0⋅V20K2=12C0V20K
Since 12C0V20=W0, we can write:
W=W0K
Final Answer
Thus, the electrostatic energy of the sphere in the dielectric is:
W=W0K
Initially, the isolated metallic object is charged in vacuum to a potential V0. The electrostatic energy associated with this charge is given as W0.
The charge q on the object can be expressed in terms of its capacitance C0 and potential V0:
q=C0⋅V0
The electrostatic energy W0 can be expressed as:
W0=12C0V20
When the metallic object is immersed in a dielectric medium with dielectric constant K, the capacitance of the object changes. The new capacitance C becomes:
C=K⋅C0
Since the charge q remains constant (as the object is isolated), we can express the new potential V in terms of the new capacitance:
V=qC=C0V0K⋅C0=V0K
The new electrostatic energy W in the dielectric can be calculated using the new capacitance and potential:
W=12CV2
Substituting the expressions for C and V:
W=12(K⋅C0)(V0K)2
Simplifying this expression:
W=12KC0⋅V20K2=12C0V20K
Since 12C0V20=W0, we can write:
W=W0K
Thus, the electrostatic energy of the sphere in the dielectric is:
W=W0K
Topper's Solved these Questions
- CAPACITANCEBOOK - RESONANCE ENGLISHCHAPTER - CAPACITANCEEXERCISE - Exercise - 3
26 Videos
- CAPACITANCEBOOK - RESONANCE ENGLISHCHAPTER - CAPACITANCEEXERCISE - High Level Problems
16 Videos
- CAPACITANCEBOOK - RESONANCE ENGLISHCHAPTER - CAPACITANCEEXERCISE - Exercise - 1
79 Videos
- ATOMIC PHYSICSBOOK - RESONANCE ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - Advanved level problems
17 Videos
- COMMUNICATION SYSTEMSBOOK - RESONANCE ENGLISHCHAPTER - COMMUNICATION SYSTEMSEXERCISE - Exercise 3
13 Videos
Similar Questions
A condenser of capacity C1 is charged to a potential V0. The electrostatic energy stored in it is U0. It is connected to another uncharged condenser of capacity C2 in parallel. The energy dissipated in the process is
View SolutionA parallel capacitor of capacitance C is charged and disconnected from the battery. The energy stored in it is E. If a dielectric slab of dielectric constant 6 is inserted between the plates of the capacitor then energy and capacitance will become.
View SolutionA parallel plate capacitor with air as dielectric is charged to a potential .v. using a battery . Removing the battery. The charged capacitor is then connected across an identical uncharged parallel plate capacitor filled with was of dielectric constant k. The common potential of both the capacitor is
View SolutionAn isolated capacitor of capacitance C is charged to a potential V. Then a dielectric slab of dielectric constant K is inserted as shown. The net charge on four surfaces 1,2, 3 and 4 would be respectively.

View SolutionA parallel plate capacitor of capacitance C is charged to a potential V and then disconnected with the battery. If separation between the plates is decreased by 50% and the space between the plates is filled with a dielectric slab of dielectric constant K=10. then
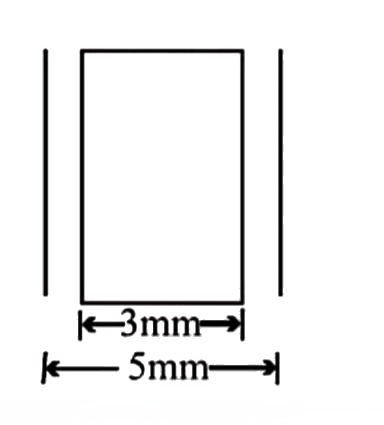
View SolutionSeparation between the plates of parallel plate capacitor is 5 mm. this capacitor, having air as the dielectric medium between the plates, is charged to a potential difference 25 V using a battery. The battery is then disconnected and a dielectric slab of thickness 3mm and dielectric constant K=10 is placed between the plates as shown. potential difference between the plates after the dielectric slab has been introduced is-
View SolutionA parallel - plate capacitor, filled with a dielectric of dielectric constant k, is charged to a potential V0. It is now disconnected from the cell and the slab is removed. If it now discharges, with time constant τ, through a resistance, then find time after which the potential difference across it will be V0?
View SolutionA capacitor is filled with an insulator and a certain potential difference is applied to its pltaes. The energy stored in the capacitor is U. Now the capacitor is disconnected from the source and the insulator is pulled out of the capacitor. The work performed against the forces of electric field in pulling out the insulator is 4U. Then dielectric constant of the insulator is.
View SolutionA parallel plate capacitor is charged to a potential difference V by a dc source. The capacitor is then disconnected from the source. If the distance between the plates in doubled, state with reason how the following will change,
(i) electric field between the plates,
(ii) capacitance and
(iii) energy stored in the capacitor.
View SolutionA parallel-plate capacitor is filled with a delectric meterial having resistivity(ρ)and dielectric constant K.The capcitor is charged and disconnected from the charging source. The capacitor is slowly discharged through the dielectric.Show that the time constant of the discharge is independent of all gepmetrical parameters like the plate area or separation between the plates. Find this time constant.
View Solution
