In a post office box if the position os the cell and the galvenometer are interchangd, then the:
null point will not change
null point will change
post office box will not work
Nothing can be said.
The correct Answer is:A
To solve the question regarding the effect of interchanging the positions of the cell and the galvanometer in a post office box, we can follow these steps:
1. Understanding the Post Office Box Setup:
- A post office box is a device used to measure the current in a circuit. It consists of a galvanometer, a cell (battery), and resistors arranged in a specific manner.
2. Identifying the Null Point:
- The null point in a post office box is the point at which the galvanometer shows zero deflection. This occurs when the potential difference across the galvanometer is zero, meaning the current through it is also zero.
3. Interchanging the Cell and Galvanometer:
- When the positions of the cell and the galvanometer are interchanged, the basic principle of the circuit remains unchanged. The galvanometer will still measure the current flowing through the circuit.
4. Analyzing the Effect of Interchange:
- The null point is determined by the ratio of resistances in the circuit and the potential difference supplied by the cell. Since these factors remain constant regardless of the position of the cell and galvanometer, the null point will not change.
5. Conclusion:
- Therefore, after interchanging the cell and galvanometer, the null point remains the same.
Final Answer:
- The correct statement is: Null point will not change.
- A post office box is a device used to measure the current in a circuit. It consists of a galvanometer, a cell (battery), and resistors arranged in a specific manner.
- The null point in a post office box is the point at which the galvanometer shows zero deflection. This occurs when the potential difference across the galvanometer is zero, meaning the current through it is also zero.
- When the positions of the cell and the galvanometer are interchanged, the basic principle of the circuit remains unchanged. The galvanometer will still measure the current flowing through the circuit.
- The null point is determined by the ratio of resistances in the circuit and the potential difference supplied by the cell. Since these factors remain constant regardless of the position of the cell and galvanometer, the null point will not change.
- Therefore, after interchanging the cell and galvanometer, the null point remains the same.
- The correct statement is: Null point will not change.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Solued miscellaneous Prolblems
8 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise-1 (Part-1)
41 Videos
- COMMUNICATION SYSTEMSBOOK - RESONANCE ENGLISHCHAPTER - COMMUNICATION SYSTEMSEXERCISE - Exercise 3
13 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP.No.71
1 Videos
Similar Questions
If in the experiment of Wheatstone's bridge, the positions of cells and galvanometer are interchanged, then balance point will
View Solutionthe post office box works on the peinclple of :
View SolutionShown in figure is a Post Office box. In order to calculate the value of external resistance, it should be connected between
View SolutionIn an experiment with a post office box, the radio of arms are 1000:10. If the value of the third resistance is 999Ω, find the unknows resistance.
View Solution
The pressures at A and B in the atmosphere are, respectively,
View SolutionWhile using a post office box the keys should be swiched on in the following order ,
View SolutionThere are 4 letters and 5 boxes in a row. Number of ways of posting these letters if all the letters are not posted in the same box is
View SolutionPassage :
Post office is useful to measure the value of unknown resistance correctly upto 2nd decimal place. It is based on Wheatstone bridge.
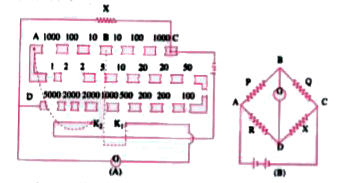
Systematic diagrams of post office box are shown in the above figures. Each of the arms AB and BC contains three resistance of 10Ω,100Ωand1000Ω. These arms are generally known as ratio arms. With the help of these resistance, we can introduce resistance P in arm AB and Resistance Q in arm BC. The resistance arm AD is complete resistance box containing resistance from 1Ωto5000Ω. In this arm, we can introduced resistance R by taking out plugs of suitable values. The unknown resistance X is connected in fourth arm CD. These four arms actually form Wheatstone bridge shown in figure. For balanced conditions, no deflection is formed in galvanometer. At balanced condition PX=QR,X=QRP
While measuring surface tension of water using capillary rise method the necessary precaution to be taken is/are
View SolutionPassage :
Post office is useful to measure the value of unknown resistance correctly upto 2nd decimal place. It is based on Wheatstone bridge.
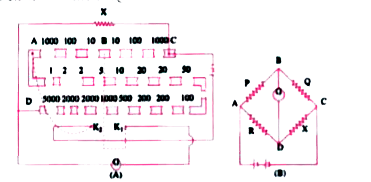
Systematic diagrams of post office box are shown in the above figures. Each of the arms AB and BC contains three resistance of 10Ω,100Ωand1000Ω. These arms are generally known as ratio arms. With the help of these resistance, we can introduce resistance P in arm AB and Resistance Q in arm BC. The resistance arm AD is complete resistance box containing resistance from 1Ωto5000Ω. In this arm, we can introduced resistance R by taking out plugs of suitable values. The unknown resistance X is connected in fourth arm CD. These four arms actually form Wheatstone bridge shown in figure. For balanced conditions, no deflection is formed in galvanometer. At balanced condition PX=QR,X=QRP
While measuring surface tension of water using capillary rise method, height of the lower meniscus from free surface of water is 3cm while inner radius of capillary tubne is found to be 0.5cm. Then compute surface tension of water using this data. [Take contact angle between glass and water as 0° and g=9.8ms−2 ]
View SolutionFor a post office box, the graph of galvanometer deflection verus (R ) (resistance pulled out of resistance box) for the ratio 100.1 is given as shown. Find the value of unknown resistance.
 .
.
View Solution
