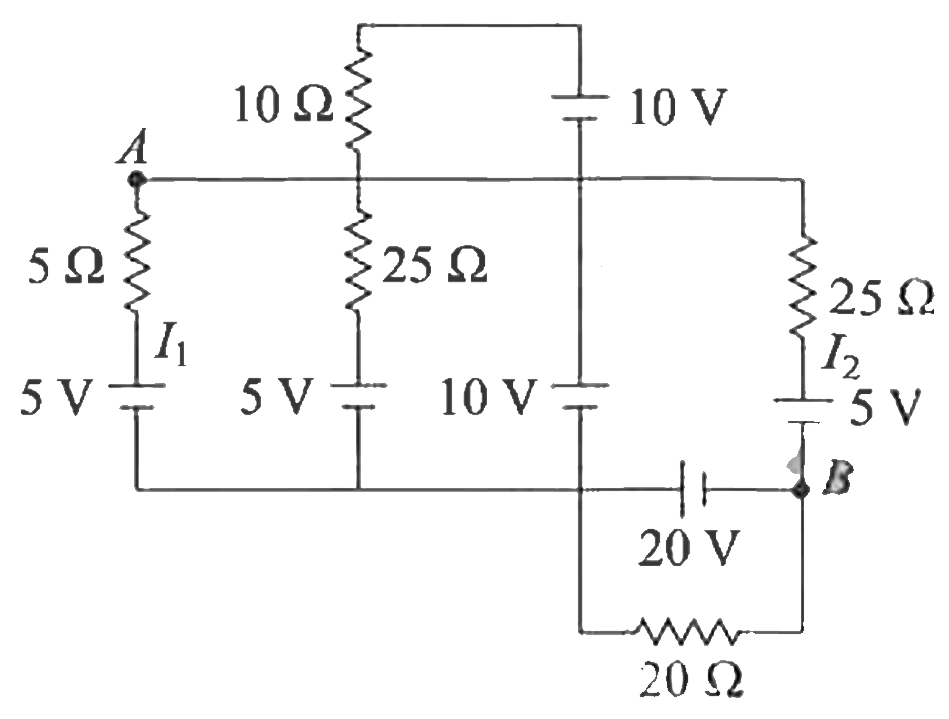
Find the current in 10Ω resistcance, V1 and source voltage Vs in the circuit shown in figure (VS=VA−VB)
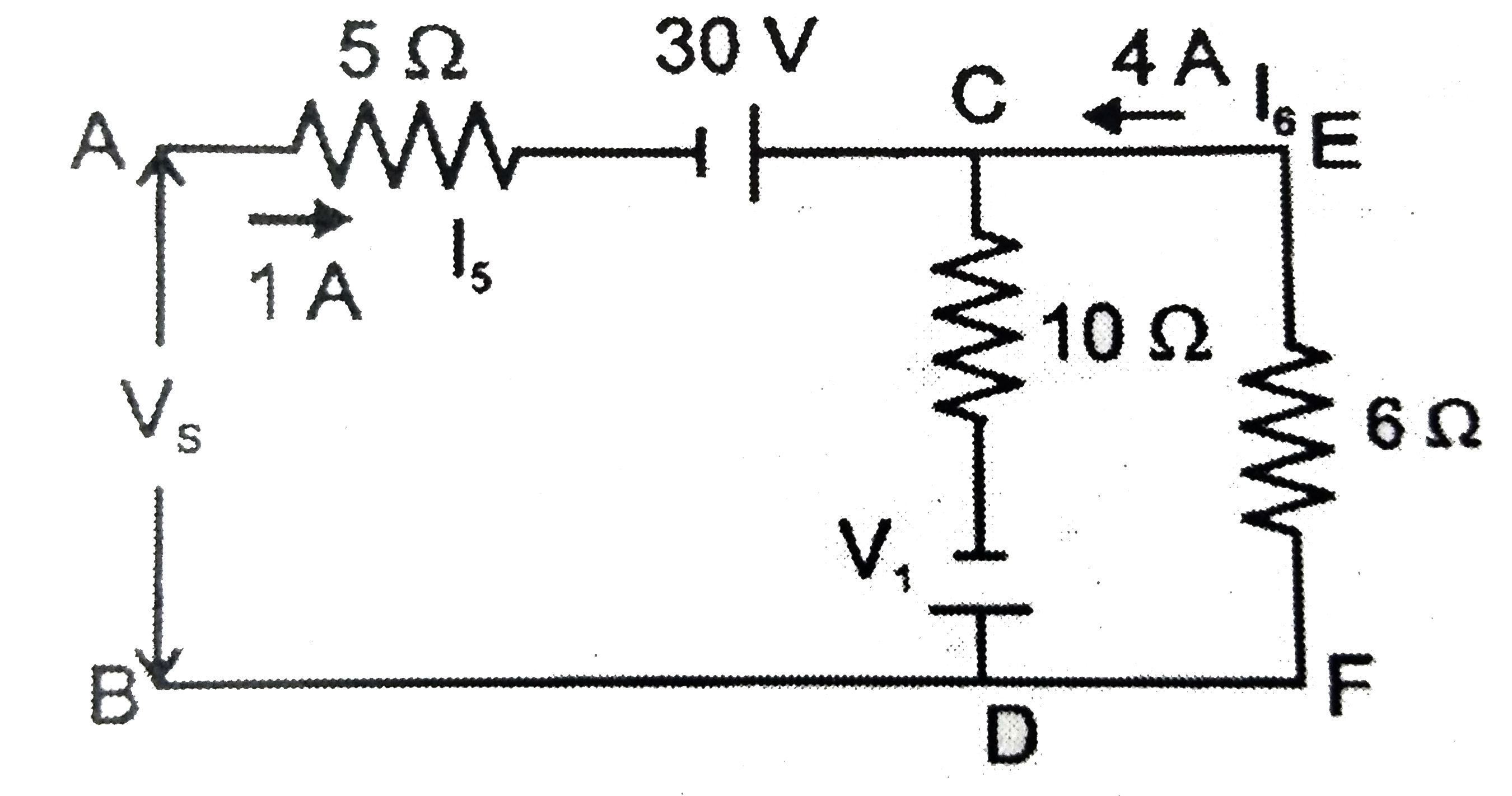
The correct Answer is:5A, 74 V, 49V( +ve terminal is connected at point B)
Step by step video & image solution for Find the current in 10Omega resistcance, V_(1) and source voltage V_(s) in the circuit shown in figure (V_(S)=V_(A)-V_(B)) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise-1 (Part-2)47videos
CURRENT ELECTRICITY
- BOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise-1 (Part-3)2videos
CURRENT ELECTRICITY
- BOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Solued miscellaneous Prolblems8videos
CURRENT ELECTRICITY
- BOOK - RESONANCE ENGLISHCHAPTER - COMMUNICATION SYSTEMSEXERCISE - Exercise 313videos
COMMUNICATION SYSTEMS
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP.No.711videos
DAILY PRACTICE PROBLEM
Similar Questions
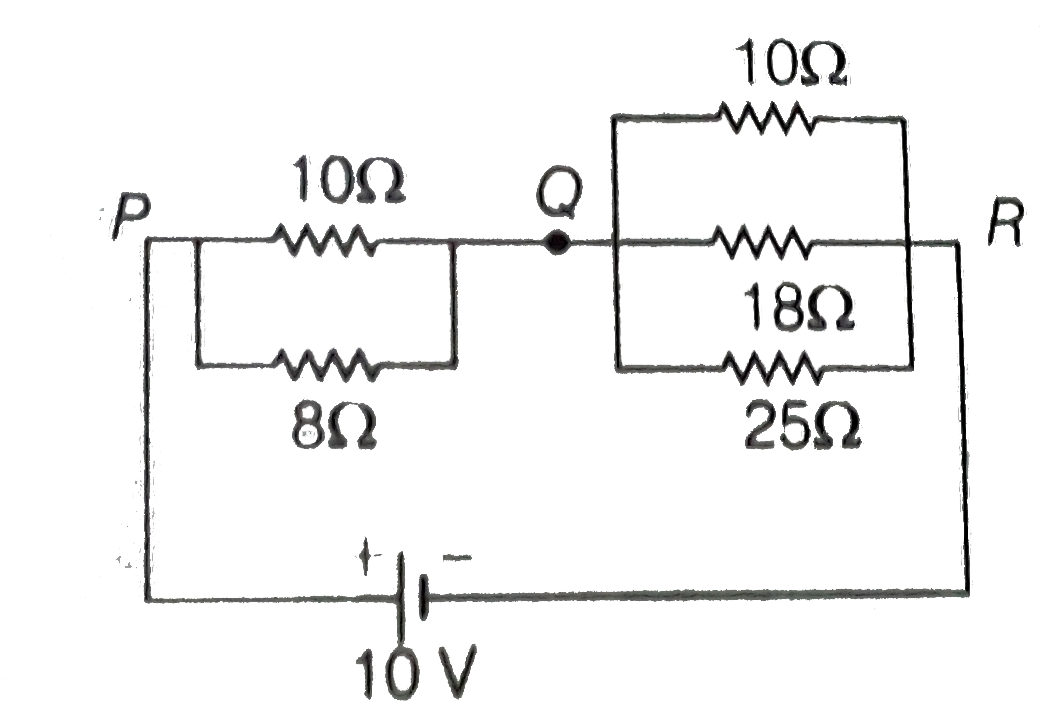
Find VP−VQ in the circuit shown in figure.
View SolutionIn the circuit shown in figure value of VR is
View SolutionIn the circuit shown in figure find Vab at 1s
View SolutionWhat is the value of output voltage V0 in the circuit shown in the figure ?
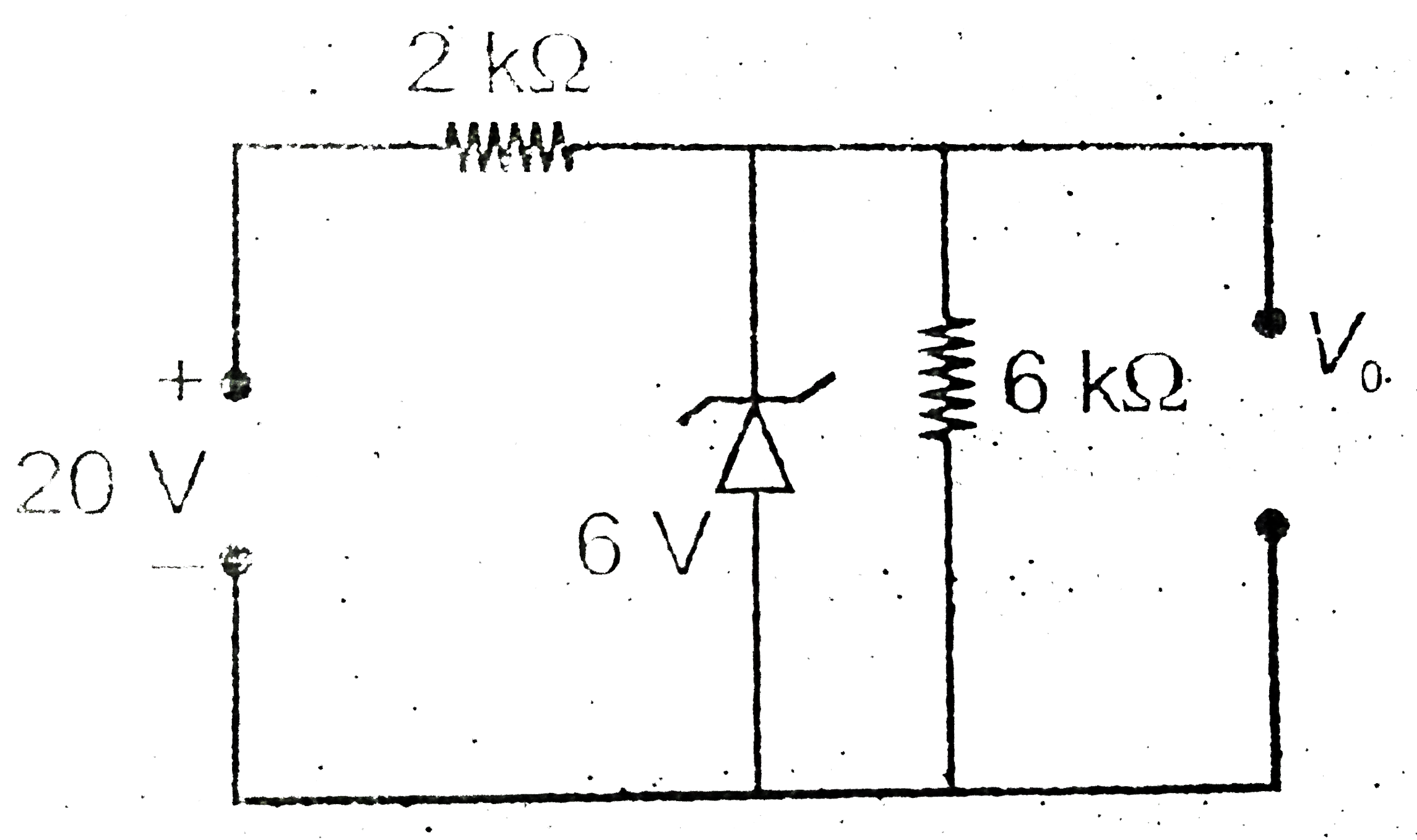
View SolutionFind the potential difference Va−Vbin the circutis shown in figure
View SolutionFind the potential difference VA−VB between points A and B of the circuit shown in figure.
View SolutionFind the potential differnce VA−VB between points A and B of the circuit shown in.
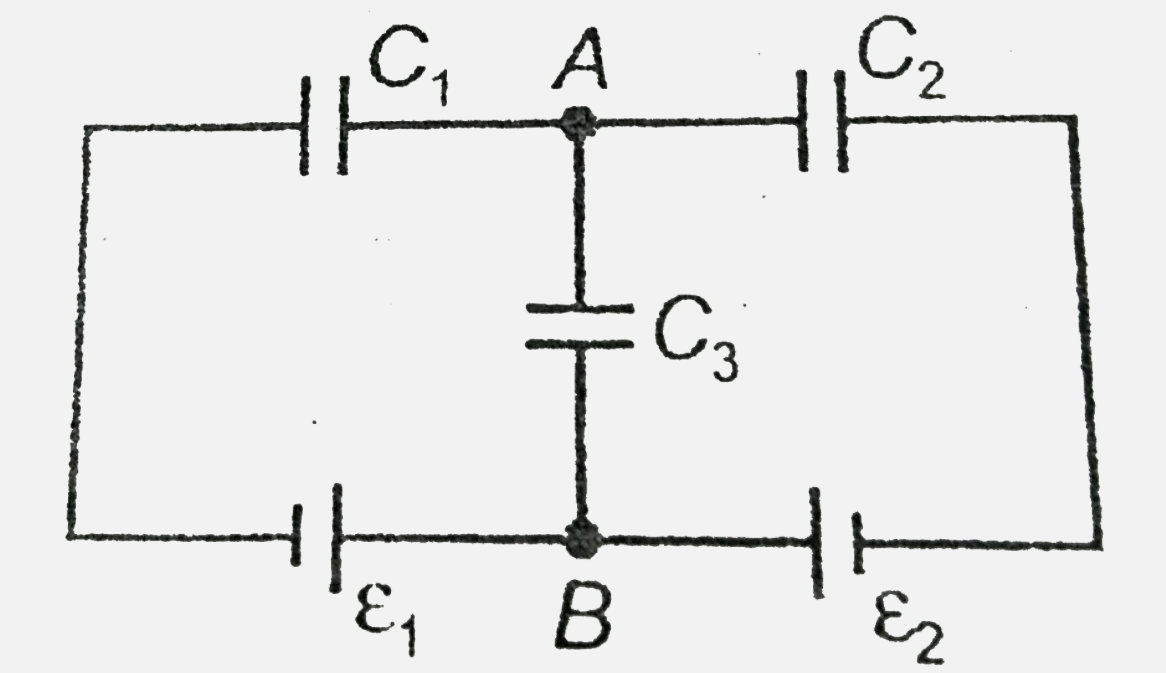
. View SolutionThe circuit consists of resistors and ideal cells. I1 and I2 are current through branches indicated in the figure, VA and VB is the potential at points A and B on the circuit
The value of VA−VB in volts is:View SolutionFind the equivalent resistance of the network shown in the figure between the points A and B if
(i) VA>VB (ii) VA<VB
View SolutionGraphical soluton of a two body head on collision
A block A of mass m moving with a uniform velocity v0 strikes another identical block B kept at rest on a horizontal smooth surface as shown in the figure (i). We can conserve linear momentum.
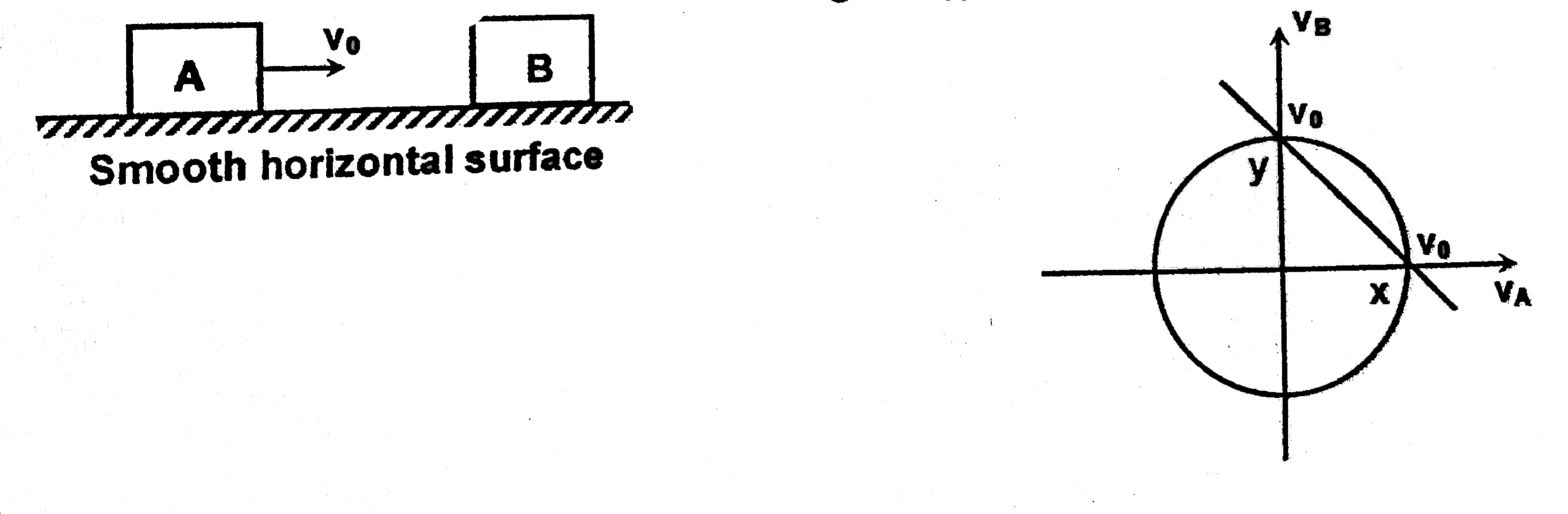
So mv0=mvAmvB (vA and vB are the velocities of the blocks after collision)
∴v0=vA+vB.........(i)
If the collision is perfectly elastic
12mv20=12mv2A+12mv2B
⇒v20=v2A+v2B......(ii)
Both the above equation (i) and (ii) are plotted on vA−vB plane as shown in figure (ii). This plot can be used to find the unknowns vA and vB.
For example the solution of the situation in figure (i) is vA=0,vB=v0 (point y in the plot)
Because vA=v0,vB=0 (point x in the plot) is not physically possible.
In a situation block A is moving with velocity 2m/s an strikes another identical block B kept at rest. The vA−vB plot for the situation is shown. m and l are the intersection points whose vA,vB coordinaes are given in the figure. The coefficient of restitution of the collision is
View Solution