A wire of resistance 0.1 cm−1 bent to form a square ABCD of side 10 cm. A simailar wire is connected between the corners B and D to form the diagonal BD. Find the effective resistance of this combination between cornaers A and C. If a 2V battery of negligible internal resistance is connected across A and C calculate the total power dissipated.
1Ω,3W
1Ω,4W
2Ω,3W
2Ω,4W
The correct Answer is:B
To solve the problem step by step, we will analyze the circuit formed by the wire and calculate the effective resistance between points A and C, and then find the power dissipated when a 2V battery is connected across A and C.
Step 1: Calculate the Resistance of Each Side of the Square
The resistance of the wire is given as 0.1 ohm per centimeter, and the length of each side of the square is 10 cm.
Rside=Resistance per cm×Length in cm=0.1Ω/cm×10cm=1Ω
Step 2: Identify the Configuration of the Circuit
The square ABCD has a wire connected along the diagonal BD. The resistances along the sides AB, BC, CD, and DA are each 1 ohm. The diagonal BD does not affect the current flow between A and C because it forms a Wheatstone bridge configuration.
Step 3: Analyze the Wheatstone Bridge Configuration
In a Wheatstone bridge, if the two opposite sides are equal, no current flows through the diagonal. Thus, the effective resistance between points A and C can be calculated by considering only the resistances along the sides AB and CD, and BC and DA.
- Resistance from A to B (R1) = 1 Ω
- Resistance from B to C (R2) = 1 Ω
- Resistance from C to D (R3) = 1 Ω
- Resistance from D to A (R4) = 1 Ω
Since the diagonal BD does not carry any current, we can simplify the circuit to two parallel resistances:
RAC=RAB+RBCandRCD+RDA
Step 4: Calculate the Effective Resistance
The two paths from A to C are:
1. A to B to C (R1 + R2 = 1 + 1 = 2 Ω)
2. A to D to C (R3 + R4 = 1 + 1 = 2 Ω)
These two paths are in parallel:
1Reffective=1RAB+RBC+1RCD+RDA=12+12=1
Thus,
Reffective=1Ω
Step 5: Calculate the Power Dissipated
Using the formula for power dissipated in a resistor:
P=V2Reffective
Substituting the values:
P=221=41=4W
Final Answers
- The effective resistance between corners A and C is 1 ohm.
- The total power dissipated is 4 watts.
The resistance of the wire is given as 0.1 ohm per centimeter, and the length of each side of the square is 10 cm.
The square ABCD has a wire connected along the diagonal BD. The resistances along the sides AB, BC, CD, and DA are each 1 ohm. The diagonal BD does not affect the current flow between A and C because it forms a Wheatstone bridge configuration.
In a Wheatstone bridge, if the two opposite sides are equal, no current flows through the diagonal. Thus, the effective resistance between points A and C can be calculated by considering only the resistances along the sides AB and CD, and BC and DA.
- Resistance from B to C (R2) = 1 Ω
- Resistance from C to D (R3) = 1 Ω
- Resistance from D to A (R4) = 1 Ω
The two paths from A to C are:
1. A to B to C (R1 + R2 = 1 + 1 = 2 Ω)
2. A to D to C (R3 + R4 = 1 + 1 = 2 Ω)
Using the formula for power dissipated in a resistor:
- The effective resistance between corners A and C is 1 ohm.
- The total power dissipated is 4 watts.
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise-1 (Part-3)2videos
CURRENT ELECTRICITY
- BOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise-2 (Part-1)24videos
CURRENT ELECTRICITY
- BOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise-1 (Part-1)41videos
CURRENT ELECTRICITY
- BOOK - RESONANCE ENGLISHCHAPTER - COMMUNICATION SYSTEMSEXERCISE - Exercise 313videos
COMMUNICATION SYSTEMS
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP.No.711videos
DAILY PRACTICE PROBLEM
Similar Questions
A write of resistance R is bent to form a square ABCD as shown in the figure. The effective resistance between E and C is :
(E is mid-point of arm CD)
 View Solution
View SolutionResistors of 1, 2, 3 ohm are connected in the form of a triangle. If a 1.5V cell of negligible internal resistance is connected across 3 ohm resistor, the current flowing through this resistance will be
View SolutionA wire of resistance 0.5ohmm−1 is bent into a circle of radius 1m. The same wire is connected across a diameter AB as shown in fig. The equivalent resistance is
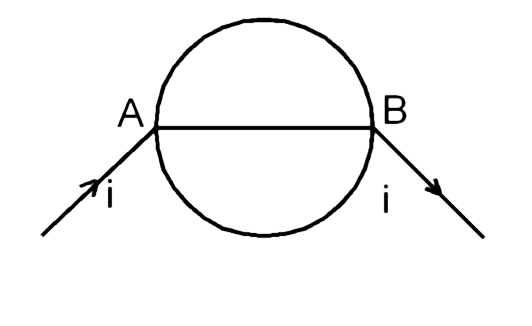 View Solution
View SolutionFour resistances of 2.0 Ω each are joined end to end, to form a square ABCD. Calculate the equivalent resistance of the combination between any two adjacent corners
View SolutionA 10 V storage battery of negligible internal resistance is connected across a 50Ω resistor. How much heat energy is produced in the resistor in 1 hour
View SolutionABCD is a square of side 'a' metres and is made of wires of resistance x ohms//metre. Similar wires are connected across the diagonals AC and BD. The effective resistance between the ax corners A and C will be
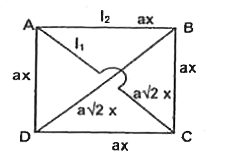 View Solution
View SolutionA wire of resistance 15.0(Ω)is bent to form a regular hexagon ABCDEFA.Find the equivalent resistance of the loop between the points (a)A and B, (b)A and C and (c )A and D .
View SolutionA wire has a resistance of 12 ohm . It is bent in the form of equilateral triangle. The effective resistance between any two corners of the triangle is
View SolutionTwo resistors A and B of resistance 4 Ω and 6 Ω respectively are connected in parallel. The combination is connected across a 6 volt battery of negligible resistance. Calculate :
the power dissipated in each resistor.View SolutionA battery of emf 2V and internal resistance 0.5(Ω)is connected across a resistance 1.5(Ω). Find the current flow through battery ?
View Solution

