1 meter long metallic wire is broken into two unequal parts PandQ.P part of the wire in uniformly extended into another wire R. Length of R is twice the length of P and the resistance of R is equal to that of Q. Find the ratio of the resistance P and R and also the ratio of the length PandQ
The correct Answer is:4
To solve the problem, let's break it down step by step.
Step 1: Define the lengths of the wire parts
Let the length of part P be L meters. Since the total length of the wire is 1 meter, the length of part Q will be:
LQ=1−L
Step 2: Define the length of wire R
According to the problem, the length of wire R is twice the length of wire P:
LR=2L
Step 3: Calculate the area of wire R
Since wire R is made from part P, we need to consider the volume conservation. The volume of wire P is equal to the volume of wire R:
Volume of P=Volume of R
AP⋅L=AR⋅LR
Substituting LR=2L:
AP⋅L=AR⋅2L
Cancelling L from both sides (assuming L≠0):
AP=2AR
Thus, the area of wire R is:
AR=AP2
Step 4: Calculate the resistance of wires P and R
The resistance R of a wire is given by the formula:
R=ρLA
Where ρ is the resistivity, L is the length, and A is the cross-sectional area.
Resistance of wire P:
RP=ρLAP
Resistance of wire R:
Substituting LR=2L and AR=AP2:
RR=ρ(2L)AR=ρ(2L)AP2=4ρLAP
Step 5: Find the ratio of the resistances RP and RR
Now we can find the ratio of the resistances:
RPRR=ρLAP4ρLAP=14
Step 6: Find the ratio of lengths P and Q
From our earlier definition, we have:
LQ=1−L
Now we can express the ratio of lengths P and Q:
LPLQ=L1−L
Since we know the resistance of wire R is equal to the resistance of wire Q, we can set up the equation:
RR=RQ
Substituting the expressions for resistance:
4ρLAP=ρ(1−L)AQ
Assuming the areas are equal (for simplicity), we can cancel ρ and rearrange:
4L=1−L
Solving for L:
5L=1⟹L=15
Thus, the length of Q is:
LQ=1−L=1−15=45
Now we can find the ratio:
LPLQ=1545=14
Final Ratios
1. The ratio of the resistances RP and RR is 14.
2. The ratio of the lengths P and Q is 14.
Let the length of part P be L meters. Since the total length of the wire is 1 meter, the length of part Q will be:
LQ=1−L
According to the problem, the length of wire R is twice the length of wire P:
LR=2L
Since wire R is made from part P, we need to consider the volume conservation. The volume of wire P is equal to the volume of wire R:
Volume of P=Volume of R
AP⋅L=AR⋅LR
Substituting LR=2L:
AP⋅L=AR⋅2L
Cancelling L from both sides (assuming L≠0):
AP=2AR
Thus, the area of wire R is:
AR=AP2
The resistance R of a wire is given by the formula:
R=ρLA
Where ρ is the resistivity, L is the length, and A is the cross-sectional area.
RP=ρLAP
Substituting LR=2L and AR=AP2:
RR=ρ(2L)AR=ρ(2L)AP2=4ρLAP
Now we can find the ratio of the resistances:
RPRR=ρLAP4ρLAP=14
From our earlier definition, we have:
LQ=1−L
Now we can express the ratio of lengths P and Q:
LPLQ=L1−L
Since we know the resistance of wire R is equal to the resistance of wire Q, we can set up the equation:
RR=RQ
Substituting the expressions for resistance:
4ρLAP=ρ(1−L)AQ
Assuming the areas are equal (for simplicity), we can cancel ρ and rearrange:
4L=1−L
Solving for L:
5L=1⟹L=15
Thus, the length of Q is:
LQ=1−L=1−15=45
Now we can find the ratio:
LPLQ=1545=14
1. The ratio of the resistances RP and RR is 14.
2. The ratio of the lengths P and Q is 14.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise-2 (Part-3)
22 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise-2 (Part-4)
12 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise-2 (Part-1)
24 Videos
- COMMUNICATION SYSTEMSBOOK - RESONANCE ENGLISHCHAPTER - COMMUNICATION SYSTEMSEXERCISE - Exercise 3
13 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP.No.71
1 Videos
Similar Questions
If a uniform wire of resistance R is uniformly strethced to n times the orginal length , then new resistance of the wire becomes
View SolutionThe diagram below shows three different modes of vibration P, Q and R of the same string of a given length.
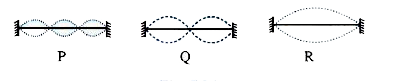
What is the ratio of the wavelength of vibrations P and R?
View SolutionIn Figure, S and T are points on the sides PQ and PR respectively of △PQR such that PT=2cm , TR=4cm and ST is parallel to QR . Find the ratio of the areas of △PST and △PQR .
View SolutionIf the pth, qth and rth terms of an A. P. are in G.P., prove that the common ratio of the G.P. is
q−rp−q.
View SolutionA piece of wire of resistance R is cut into five equal parts. These parts are then connected in parallel. If the equivalent resistance of this combination is R', then the ratio R/R' is :
View SolutionGiven that P 12, Q = 5 and R = 13 also P+Q=R, then the angle between P and Q will be
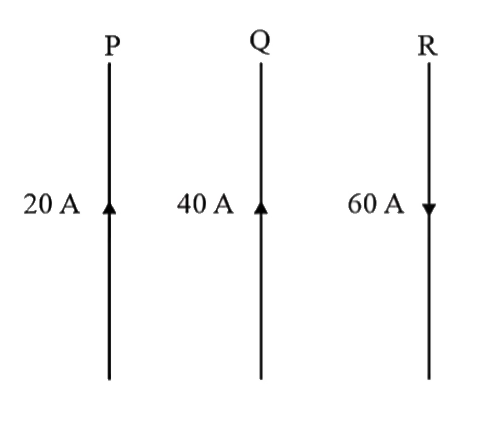
View SolutionP, Q and R are long straight wires in air, carrying currents as shown. The force on Q is directed
View SolutionIn two similar triangles ABC and PQR , if their corresponding altitudes AD and PS are in the ratio 4:9, find the ratio of the areas of triangle ABC and triangle PQR .
View SolutionLet p,qandr be three statements, then (~p→q)→r is equivalent to
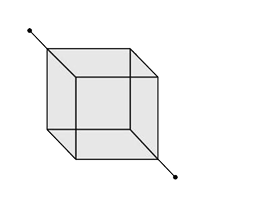
View SolutionTwelve wires of equal length and same cross-section are connected in the form of a cube. If the resistance of each of the wires is R, and the effective resistance between the two diagonal ends is Re, then the ratio RRe is equal to __.
View Solution
