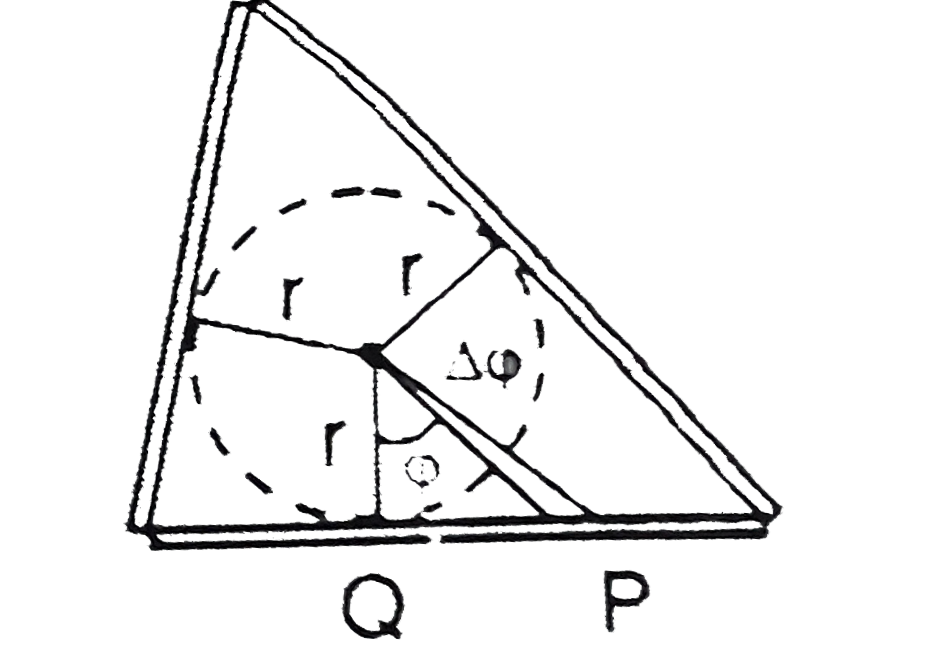
A triangle is made from thin insulating rods of different lengths, and the rods are uniformly charged, i.e. the linear charge density on each rod is uniform and the same for all three rods. Find a particular point in the plane of the triangle at which the electric field strength is zero
We are going to prove that the electric field strength is zero at the socalled incentre, the centre of the triangle's inscribed circle (which has radius r in the figure)
Let us consider a small length of rod at position P on one of the sides of the triangle, let it subtend an angle Δφ at the incentre (see figure). Its distance from the incentre is r/cosφ. Its small length Δx can be found by noting that P is a distance x=rtanφ along the rod from the fixed point Q and so Δx=(rΔφ)/(cos2φ). Consequently the charge it carries is Δq=λrΔφcos2φ
where λ is the linear charge density on the rods. The magnitude of the elementary contribution of this small piece to the electric field at the incentre is ΔE=14πε0Δqcos2φr2=14πε0λrΔφr2
It can be seen from this result that the same electric field (in both magnitude and direction) would be produced by an arc of the inscribed circle that subtends Δφ at the circle's centre and carries the same linear charge density λ as the rod.
Summing up the contributions of the small arc pieces correspondingto all threesides of the triangle, we will, because of the circular symmetry, obatin zero net field. It follows that the electric field strength produced by the charges sides of the triangle is also zero at the incentre.
Topper's Solved these Questions
- ELECTROSTATICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Part - II
23 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - A.l.P
19 Videos
- EXPERIMENTAL PHYSICSBOOK - RESONANCE ENGLISHCHAPTER - EXPERIMENTAL PHYSICSEXERCISE - PART -II
10 Videos
Similar Questions
Calculate the potential due to a thin uniformly charged rod of length L at the poiot P shown in figure. The lioear charge density of the rod is λC/m

View Solutionthe linear charge density of a thin metallic rod varies with the distance x from the end as λ=λ0x2(0≤x≤l) The total charge on the rod is
View Solution
Knowledge Check
the linear charge density of a thin metallic rod varies with the distance x from the end as λ=λ0x2(0≤x≤l) The total charge on the rod is
Aλ0l33Bλ0l34C2λ0l33Dλ0l32
An insulating rod of uniform linear charge density A and uniform linear mass density μ lies on a smooth table whose surface is xy-plane. A uniform electric field E is switched on in the space:

View SolutionCalculate the potential at a point on the perpendicular bisector of uniformly charged thin rod (linear density of charge =λ) of length 2l at a distance a from the centre of the rod.
View SolutionA uniformly charged non conducting rod is suspended vertically at its end. The rod can swing freely in the vertical plane without any friction. The linear charge density on the rod is λC/m and it has a uniformly distributed mass of M
Length of the rod is L. A uniform horizontal electrif field (E) is switched on in the region.
(a). For what value of electric field (call it E0) the rod just manages to make itself horizontal.?
(b). If eletrif field E0 is switched on, what is the maximum angular speed acquired by the rod during its motion?

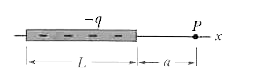
View SolutionIn Fig., a nonconducting rod of length L = 8.15 cm has a charge -q = -4.23 fC uniformly distributed along its length. (a) What is the linear charge density of the rod ? What are the (b) magnitude and (c ) direction (relative to the positive direction of the x axis) of the electric field produced at point P, at distance a = 6.00 cm from the rod ? What is the electric field magnitude produced at distance a = 50 m by (d) the rod and (e) a particle of charge -q = -4.23 fC that we use to replace the rod ? (At that distance, the rod "looks" like a particle.)
View SolutionCalculate the potential due to a thin charged rod of length L at the points along and perpendicular to the length. Charge per unit length on the rod is λ.

View SolutionCalculate the potential due to a thin charged rod of length L at the points along and perpendicular to the length. Charge per unit length on the rod is λ.

View SolutionIn the figure shown S is a large nonconducting sheet of uniform charge density σ. A rod R of length l and mass 'm' is parallel to the sheet and hinged at its mid point. The linear charge densities on the upper and lower half of the rod are shown in the figure. Find the angular acceleration of the rod just after it is released.
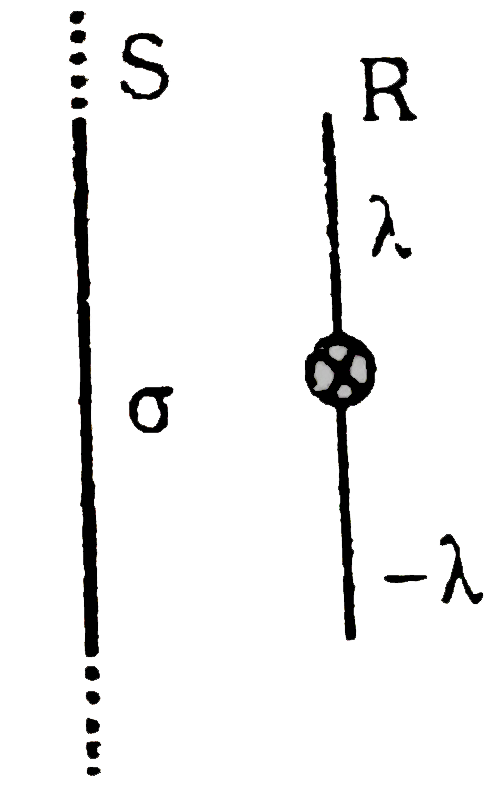
View Solution
