Two small metallic balls of radii R1&R2 are kept in vacuum at a large distance compared to the radii. Find the ratio between the charges on the two balls at which electrostatic energy of the system is minimum. What is the potential difference between the two balls ? total charge of balls is constant.
The correct Answer is:Q1Q2=R1R2;0
To solve the problem, we need to find the ratio of the charges on two metallic balls such that the electrostatic energy of the system is minimized. We will also determine the potential difference between the two balls.
1. Understanding the System:
- We have two metallic balls with radii R1 and R2.
- Let the charges on the balls be q1 and q2 respectively.
- The total charge q is constant, so q1+q2=q.
2. Electrostatic Energy Calculation:
- The electrostatic energy U of the system consists of self-energy and interaction energy.
- The self-energy of each ball is given by:
Uself=kq212R1+kq222R2
- The interaction energy between the two balls (since they are at a large distance) is negligible.
3. Total Electrostatic Energy:
- Thus, the total electrostatic energy U can be expressed as:
U=kq212R1+kq222R2
4. Substituting q2:
- Since q2=q−q1, we can substitute this into the energy equation:
U=kq212R1+k(q−q1)22R2
5. Differentiating to Find Minimum Energy:
- To find the minimum energy, we differentiate U with respect to q1 and set the derivative to zero:
dUdq1=kq1R1−k(q−q1)R2=0
6. Solving the Derivative Equation:
- Rearranging gives:
q1R1=q−q1R2
- Cross-multiplying yields:
q1R2=(q−q1)R1
- Expanding and rearranging gives:
q1(R1+R2)=qR1
- Thus, we find:
q1=qR1R1+R2
- Consequently, for q2:
q2=q−q1=qR2R1+R2
7. Finding the Ratio of Charges:
- The ratio of the charges q1q2 is:
q1q2=qR1R1+R2qR2R1+R2=R1R2
8. Potential Difference Calculation:
- The potential V1 on ball 1 is given by:
V1=q14πϵ0R1
- The potential V2 on ball 2 is given by:
V2=q24πϵ0R2
- The potential difference V between the two balls is:
V=V1−V2=q14πϵ0R1−q24πϵ0R2
Final Results:
- The ratio of the charges is:
q1q2=R1R2
- The potential difference V can be calculated using the expressions for V1 and V2.
- We have two metallic balls with radii R1 and R2.
- Let the charges on the balls be q1 and q2 respectively.
- The total charge q is constant, so q1+q2=q.
- The electrostatic energy U of the system consists of self-energy and interaction energy.
- The self-energy of each ball is given by:
Uself=kq212R1+kq222R2
- The interaction energy between the two balls (since they are at a large distance) is negligible.
- Thus, the total electrostatic energy U can be expressed as:
U=kq212R1+kq222R2
- Since q2=q−q1, we can substitute this into the energy equation:
U=kq212R1+k(q−q1)22R2
- To find the minimum energy, we differentiate U with respect to q1 and set the derivative to zero:
dUdq1=kq1R1−k(q−q1)R2=0
- Rearranging gives:
q1R1=q−q1R2
- Cross-multiplying yields:
q1R2=(q−q1)R1
- Expanding and rearranging gives:
q1(R1+R2)=qR1
- Thus, we find:
q1=qR1R1+R2
- Consequently, for q2:
q2=q−q1=qR2R1+R2
- The ratio of the charges q1q2 is:
q1q2=qR1R1+R2qR2R1+R2=R1R2
- The potential V1 on ball 1 is given by:
V1=q14πϵ0R1
- The potential V2 on ball 2 is given by:
V2=q24πϵ0R2
- The potential difference V between the two balls is:
V=V1−V2=q14πϵ0R1−q24πϵ0R2
- The ratio of the charges is:
q1q2=R1R2
- The potential difference V can be calculated using the expressions for V1 and V2.
Topper's Solved these Questions
- ELECTROSTATICSBook:RESONANCE ENGLISHChapter:ELECTROSTATICSExercise:Part - II
Explore 23 Videos
- ELECTROMAGNETIC INDUCTIONBook:RESONANCE ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:A.l.P
Explore 19 Videos
- EXPERIMENTAL PHYSICSBook:RESONANCE ENGLISHChapter:EXPERIMENTAL PHYSICSExercise:PART -II
Explore 10 Videos
Similar Questions
Two point charges 2q and 8q are placed at a distance r apart. Where should a third charge −q be placed between them so that the electrical potential energy of the system is a minimum
View SolutionTwo metallic s pheres of radii R1 and R2 are connected b y a thin wire. If +q1~and+q_(2) are the charges on the two s pheres then
View SolutionTwo concentric conducting spheres of radii R and 2R are crrying charges Q and −2Q, respectively. If the charge on inner sphere is doubled, the potetial differece between the two spheres will
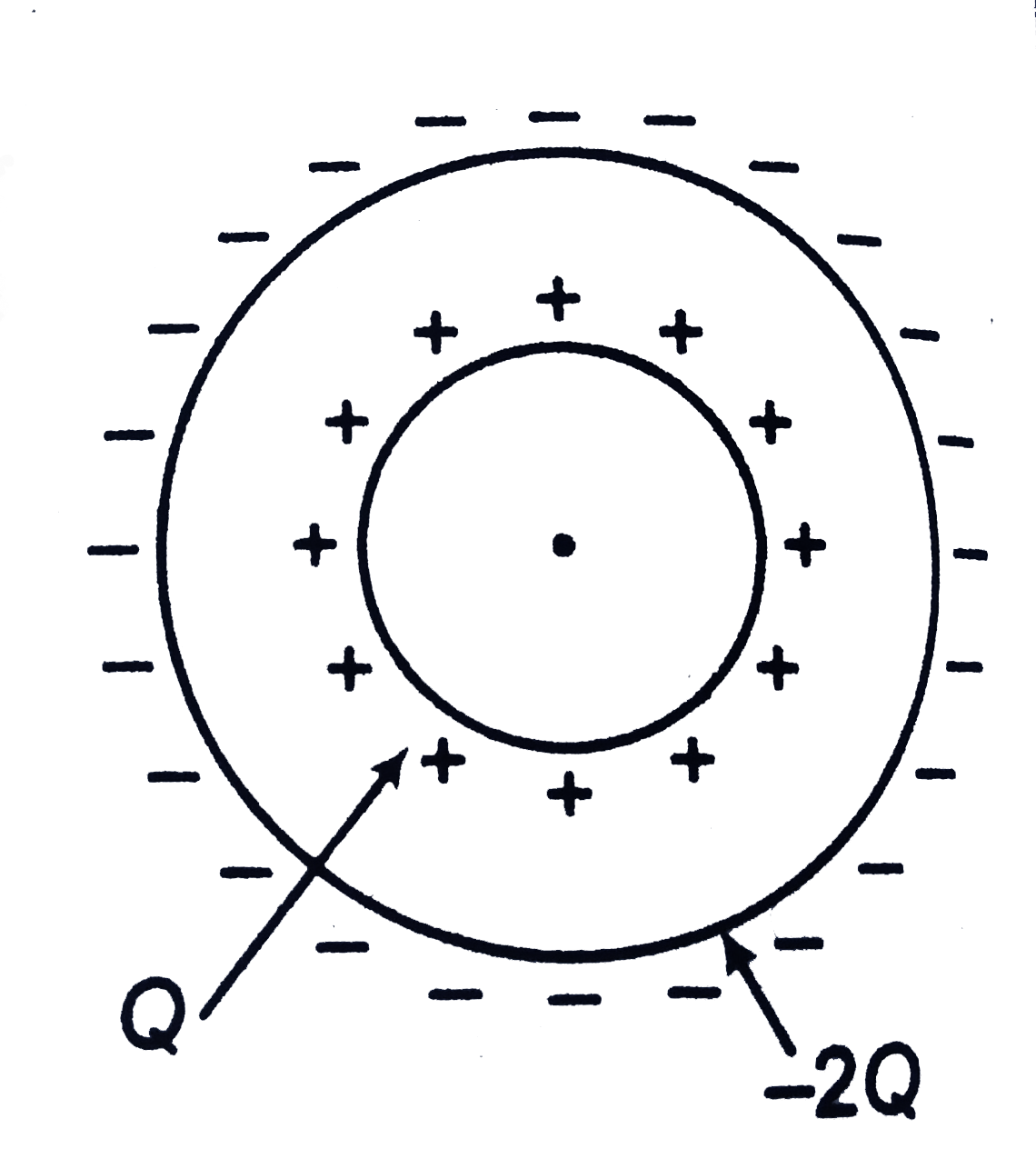
View SolutionTwo charged spheres of radii R1andR2 having equal surface charge density. The ratio of their potential is
View SolutionTwo spheres of radii R1 and R1 respectively are charged and joined by wire. The ratio of electric field of spheres is
View SolutionThree plates A, B and C are placed close to each other with +Q charge given to the middle plate. The inner surfaces to A and C can be connected to earth through plate D and keys K1 and K2 . The plates D is a dielectric slab with dielectric constant K1 then the charge that will flow through plate D and keys K1 and K2 . The plate D is a dielectric slab with dielectric constant K, then the charge that will flow though plate D when K2 is closed and K2 is open is

View SolutionThe position vectors of two balls are given by
→r1=2(m)i+7(m)j
→r2=−2(m)i+4(m)j
What will be the distance between the two balls?
View SolutionThe position vectors of two balls are given by
→r1=2(m)i+7(m)j
→r2=−2(m)i+4(m)j
What will be the distance between the two balls?
View SolutionTwo balls, each of radius R, equal mass and density are placed in contact, then the force of gravitation between them is proportional to
View SolutionTwo balls, each of radius R, equal mass and density are placed in contact, then the force of gravitation between them is proportional to
View Solution