Supose a planet is revolving around the sun in an elliptical path given by x2a2+y2b2=1
Find time period of revolution Angular momentum of the planet about the sun is L
 .
.
Rate of area swept dAdt=L2m =constant
⇒dA=L2mdt
A=πab∫A=0dA=t=T∫t=0L2mdt
⇒πab=L2mT⇒T=2πmabL .
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - GRAVITATIONEXERCISE - SOLVED MISCELLANEOUS PROBLEMS5videos
GRAVITATION
- BOOK - RESONANCE ENGLISHCHAPTER - GRAVITATIONEXERCISE - EXAMPLE2videos
GRAVITATION
- BOOK - RESONANCE ENGLISHCHAPTER - GEOMATRICAL OPTICS EXERCISE - Advance level Problems35videos
GEOMATRICAL OPTICS
- BOOK - RESONANCE ENGLISHCHAPTER - NUCLEAR PHYSICSEXERCISE - Advanced level solutions16videos
NUCLEAR PHYSICS
Similar Questions
A planet is revolving around the sun as shown in elliptical path. The correct option is
 View Solution
View SolutionA planet is revolving around the sun in an elliptical orbit having eccentricity e(=π4). If the time period of revolution is 16 months then find the time taken by the planet in going from A to B in months.
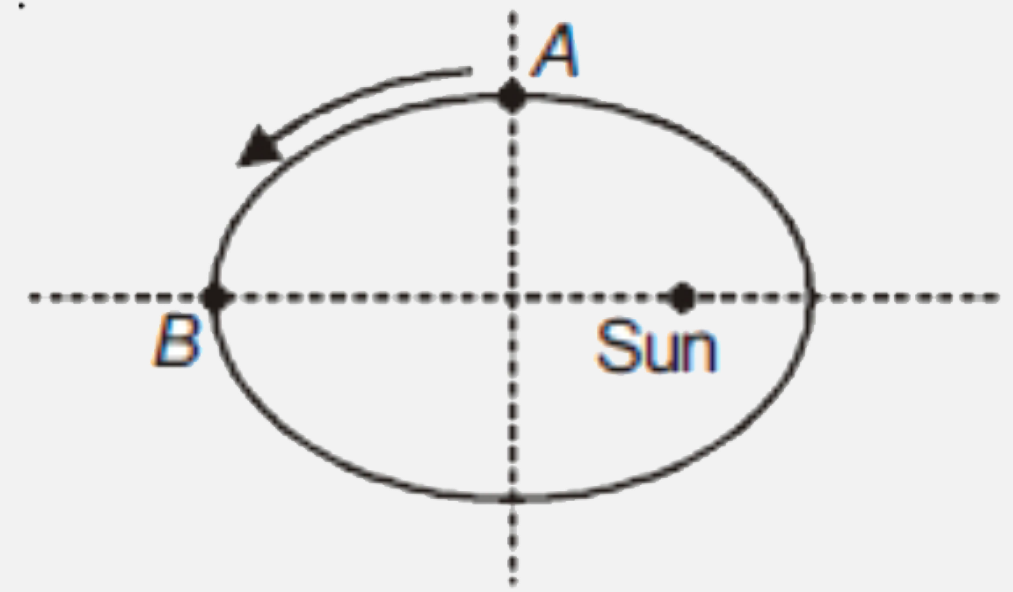 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A planet revolves around the sun in elliptical orbit of eccentricity 'e'. If 'T' is the time period of the planet then the time spent by the planet between the ends of the minor axis and major axis close to the sun is
ATπ2eBT(2eπ−1)CTe2πDT(14−e2π) - Question 2 - Select One
A planet revolves around the sun in an elliptical orbit. Suppose that the gravitational attraction between the sun and the planet suddenly disappear then the planet would move
Atowards the sun in a spiral pathBaway from the sun along a straight path with continuously increasing speedCwith constant speed along a tangential path to the oribtDtowards the sun along a straight path with constant speed - Question 3 - Select One
If the earth is a point mass of 6×1024 kg revolving around the sun at a distance of 1.5×108 km and in time T=3.14×107 s, then the angular momentum of the earth around the sun is
A1.2×1018kgm2/sB1.8×1029kgm2/sC1.5×1037kgm2/sD2.7×1040kgm2/s
A planet revolves around the sun in an elliptical . The linear speed of the planet will be maximum at
 View Solution
View SolutionA planet is revolving around the Sun in an elliptical orbit. Its closest distance from the Sun is r and farthest distance is R. If the orbital velocity of the planet closest to the Sun is v, then what is the velocity at the farthest point?
View SolutionFor a planet revolving around Sun in an elliptical orbit, to obtain its velocity at any point we have to apply
View SolutionA: The speed of a planet is maximum at perihelion .
R : The angular momentum of a planet about centre of sun is conserved .View SolutionIf the earth is a point mass of 6×1024kg revolving around the sun at a distance of 1.5×108km and in time, T=3.14×107s, then the angular momentum of the earth around the sun is
View Solution

