A LCR circuit behaves like a damped harmonic oscillator. Comparing it with a physical spring mass damped oscillator having damping constant ‘b’. If the amount of initial charge on the capacitor be Q0. then the amplitude of the amount of charge on the capacitor as a function of time t will be:
Q=Q0e−Rt2l
Q=Q0(1−e−2RtL)
Q=Q0e−RtL
Q=Q0(1−e−RtL)
The correct Answer is:A
To find the amplitude of the amount of charge on the capacitor as a function of time t in an LCR circuit behaving like a damped harmonic oscillator, we can follow these steps:
1. Understand the Damped Harmonic Oscillator:
In a damped harmonic oscillator, the motion can be described by the second-order differential equation:
md2xdt2+bdxdt+kx=0
where m is the mass, b is the damping constant, and k is the spring constant.
2. Amplitude Decay in Damped Oscillation:
The general solution for the amplitude A(t) of a damped oscillator is given by:
A(t)=A0e−b2mt
where A0 is the initial amplitude.
3. Apply to the LCR Circuit:
In the context of an LCR circuit, we can relate the parameters:
- Replace m with L (inductance),
- Replace b with R (resistance),
- Replace k with 1C (capacitance).
4. Write the Equation for Charge:
The charge Q(t) on the capacitor as a function of time can be expressed as:
Q(t)=Q0e−R2Lt
where Q0 is the initial charge on the capacitor.
5. Final Expression:
Thus, the amplitude of the charge on the capacitor as a function of time t is:
Q(t)=Q0e−R2Lt
Final Result:
The amplitude of the amount of charge on the capacitor as a function of time t is:
Q(t)=Q0e−R2Lt
In a damped harmonic oscillator, the motion can be described by the second-order differential equation:
md2xdt2+bdxdt+kx=0
where m is the mass, b is the damping constant, and k is the spring constant.
The general solution for the amplitude A(t) of a damped oscillator is given by:
A(t)=A0e−b2mt
where A0 is the initial amplitude.
In the context of an LCR circuit, we can relate the parameters:
- Replace m with L (inductance),
- Replace b with R (resistance),
- Replace k with 1C (capacitance).
The charge Q(t) on the capacitor as a function of time can be expressed as:
Q(t)=Q0e−R2Lt
where Q0 is the initial charge on the capacitor.
Thus, the amplitude of the charge on the capacitor as a function of time t is:
Q(t)=Q0e−R2Lt
The amplitude of the amount of charge on the capacitor as a function of time t is:
Q(t)=Q0e−R2Lt
Topper's Solved these Questions
Similar Questions
An LCR circuit behaves like a damped harmonic oscillator. Comparing it with a physical spring mass damped oscillator having damping constant b, the correct equivalence of b would be:
View SolutionAn LCR circuit behaves like a damped harmonic oscillator. Comparing it with a physical spring mass damped oscillator having damping constant b, the correct equivalence of b would be:
View SolutionAn LCR series circuit behaves like a damped harmonic oscillator. Comparing it with a physical spring-mass damped oscillator having damping constant ‘b’, the correct equivalence would be (Take, i = current, V = voltage, x = displacement, q = charge, F = force, v = velocity)
View SolutionInitially the capacitor is uncharged find the charge on capacitor as a function of time, if switch is closed at t=0.

View SolutionA LCR circuit be haves like a damped harmonic oscillator. The discharge of capacitor C, through an C□ inductor L having resistance R is oscillatory. Then which of following is correct _____.
View SolutionA LCR circuit be haves like a damped harmonic oscillator. The discharge of capacitor C, through an C□ inductor L having resistance R is oscillatory. Then which of following is correct _____.
View SolutionTime constant of a C-R circuit is 2ln(2) second. Capacitor is discharged at time t=0. The ratio of charge on the capacitor at time t=2s and t=6s is
View SolutionA capacitor of capacitance C is given a charge Q. At t=0,it is connected to an uncharged of equal capacitance through a resistance R. Find the charge on the second capacitor as a function of time.
View SolutionA capacitor with capacitance 6×10−5F is charged by connecting it to a 12−V battery. The capacitor is disconnected from the battery and connected across an inductor with L=1.50H.
a. What are the angular frequency ω of the electrical oscillations and the period of these oscillations (the time for one oscillation)?
b. What is the intial charge on the capacitor?
c. How much energy is intially stored in the capacitor?
d. What is the charge on the capacitor 0.0230 s after the connecting to the inductor is made? Interpret the sign of the your answer.
e. At the times given in part (d), what is the current in the inductor? Interpret the sign of your answer.
f. At the time given in part (d), how much electrical energy is stored in the capactior and how much is stored in the inductor?
View SolutionIn the circuit shown, the capacitor C1 is initially charged with charge q0. The switch S is closed at time t = 0 . The charge on C2 after time t is
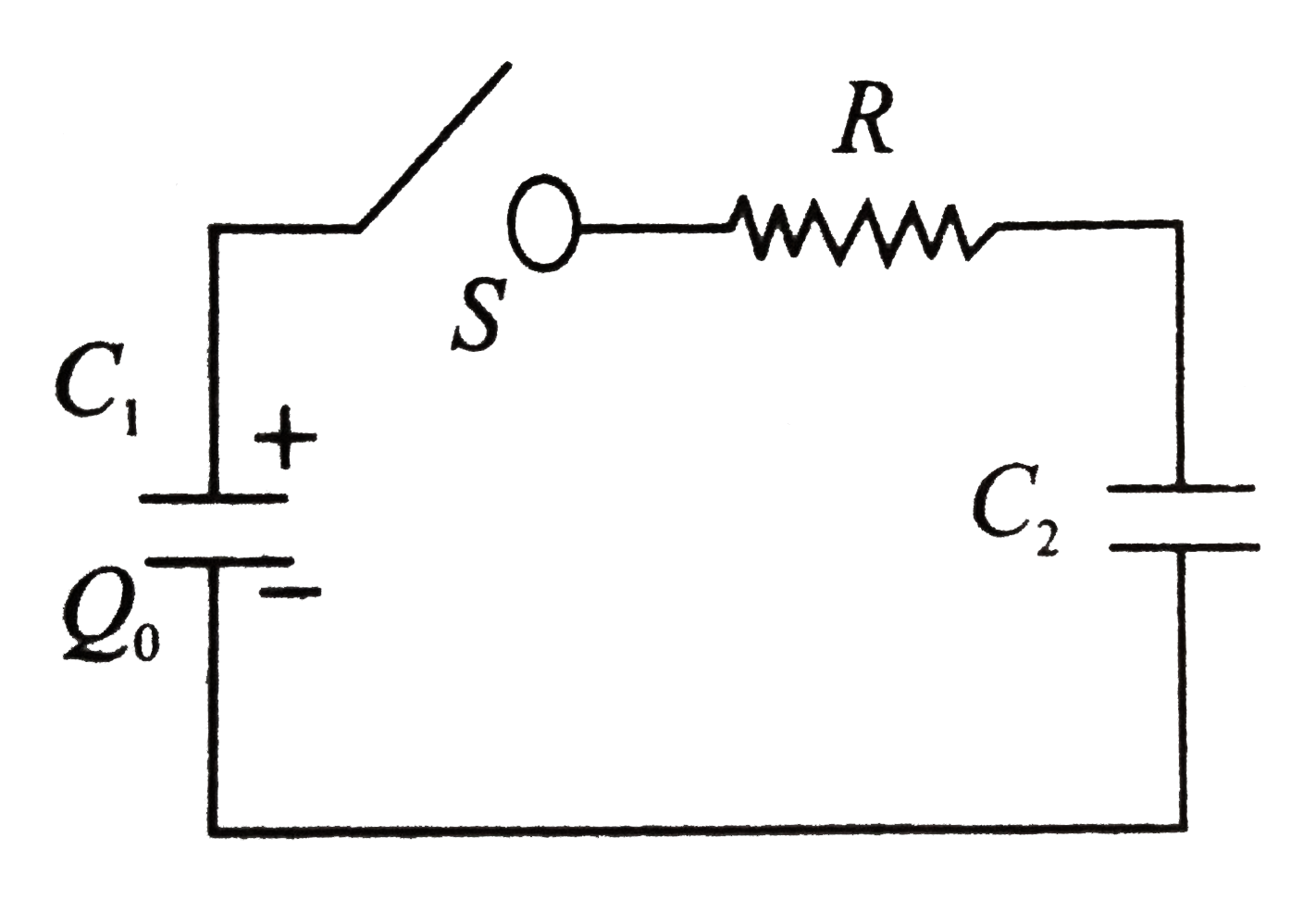
View Solution
