A LCR circuit be haves like a damped harmonic oscillator. The discharge of capacitor C, through an C□ inductor L having resistance R is oscillatory. Then which of following is correct _____.
1LC<R24L2
1LC>R24L2
1LC>R34L4
1√LC>R38
The correct Answer is:B
To solve the problem regarding the behavior of an LCR circuit as a damped harmonic oscillator, we will derive the necessary equations and conditions step by step.
1. Understanding the LCR Circuit:
- An LCR circuit consists of an inductor (L), a capacitor (C), and a resistor (R) connected in series. When the capacitor discharges through the inductor, the energy oscillates between the capacitor and the inductor.
2. Writing the Voltage Equation:
- According to Kirchhoff's loop rule, the sum of potential differences around the circuit must equal zero:
VL+VR+VC=0
- Where:
- VL=LdIdt (voltage across the inductor)
- VR=IR (voltage across the resistor)
- VC=QC (voltage across the capacitor)
3. Substituting Current:
- The current I is the rate of flow of charge Q, so I=dQdt.
- Substituting this into the equation gives:
Ld2Qdt2+RdQdt+QC=0
4. Forming the Differential Equation:
- Rearranging the terms leads to the second-order differential equation:
Ld2Qdt2+RdQdt+QC=0
5. Identifying the Damped Oscillation:
- The general solution to this equation indicates that the charge Q oscillates and can be expressed as:
Q(t)=Q0e−R2Ltcos(ωt)
- Here, ω is the angular frequency of oscillation.
6. Finding the Angular Frequency:
- The angular frequency ω is given by:
ω=√1LC−(R2L)2
7. Condition for Oscillation:
- For oscillation to occur, the term under the square root must be positive:
1LC−(R2L)2>0
- Rearranging this gives:
1LC>R24L2
8. Conclusion:
- Therefore, the correct condition that must be satisfied for the LCR circuit to behave as a damped harmonic oscillator is:
1LC>R24L2
- This implies that option (b) is correct.
- An LCR circuit consists of an inductor (L), a capacitor (C), and a resistor (R) connected in series. When the capacitor discharges through the inductor, the energy oscillates between the capacitor and the inductor.
- According to Kirchhoff's loop rule, the sum of potential differences around the circuit must equal zero:
VL+VR+VC=0
- Where:
- VL=LdIdt (voltage across the inductor)
- VR=IR (voltage across the resistor)
- VC=QC (voltage across the capacitor)
- The current I is the rate of flow of charge Q, so I=dQdt.
- Substituting this into the equation gives:
Ld2Qdt2+RdQdt+QC=0
- Rearranging the terms leads to the second-order differential equation:
Ld2Qdt2+RdQdt+QC=0
- The general solution to this equation indicates that the charge Q oscillates and can be expressed as:
Q(t)=Q0e−R2Ltcos(ωt)
- Here, ω is the angular frequency of oscillation.
- The angular frequency ω is given by:
ω=√1LC−(R2L)2
- For oscillation to occur, the term under the square root must be positive:
1LC−(R2L)2>0
- Rearranging this gives:
1LC>R24L2
- Therefore, the correct condition that must be satisfied for the LCR circuit to behave as a damped harmonic oscillator is:
1LC>R24L2
- This implies that option (b) is correct.
Topper's Solved these Questions
- MOCK TEST 10BOOK - VMC MODULES ENGLISHCHAPTER - MOCK TEST 10EXERCISE - PHYSICS (SECTION 2)
5 Videos
- MOCK TEST 1BOOK - VMC MODULES ENGLISHCHAPTER - MOCK TEST 1EXERCISE - PART I : PHYSICS (SECTION-2)
10 Videos
- MOCK TEST 11BOOK - VMC MODULES ENGLISHCHAPTER - MOCK TEST 11EXERCISE - Physics (Section-2)
5 Videos
Similar Questions
in series R-L-C circuit at resonance, which of the following is correct?
View SolutionAn LCR circuit behaves like a damped harmonic oscillator. Comparing it with a physical spring mass damped oscillator having damping constant b, the correct equivalence of b would be:
View SolutionAn LCR circuit behaves like a damped harmonic oscillator. Comparing it with a physical spring mass damped oscillator having damping constant b, the correct equivalence of b would be:
View SolutionA LCR circuit behaves like a damped harmonic oscillator. Comparing it with a physical spring mass damped oscillator having damping constant ‘b’. If the amount of initial charge on the capacitor be Q0. then the amplitude of the amount of charge on the capacitor as a function of time t will be:
View SolutionA LCR circuit behaves like a damped harmonic oscillator. Comparing it with a physical spring mass damped oscillator having damping constant ‘b’. If the amount of initial charge on the capacitor be Q0. then the amplitude of the amount of charge on the capacitor as a function of time t will be:
View SolutionAn LCR series circuit behaves like a damped harmonic oscillator. Comparing it with a physical spring-mass damped oscillator having damping constant ‘b’, the correct equivalence would be (Take, i = current, V = voltage, x = displacement, q = charge, F = force, v = velocity)
View SolutionFigure below shows a capacitor C, an inductor L and a resistor R, connected in series to an a.c. supply of 220 V.
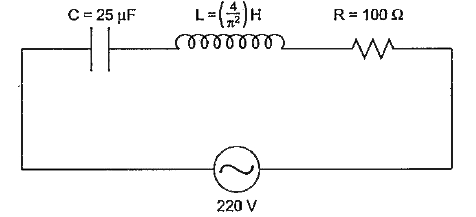
Current flowing through the circuit.
View SolutionAn inductor L is allowed to discharge through capacitor C. The emf induced across the inductance when the capacitor is fully charged is
View SolutionA resistance (R = 12 omega), an inductor (L = 2 H) and a capacitor (C = 5 muF) are connected to an AC generator of frequency 50 Hz. Which of the following statement is correct
View SolutionFigure below shows a capacitor C, an inductor L and a resistor R, connected in series to an a.c. supply of 220 V.
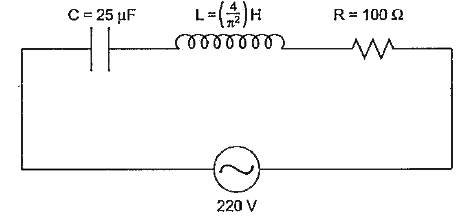
Average power consumed by the circuit.
View Solution
